2.2 Визначення інтенсивності відмов
Після середнього напрацювання на відмову другою важливою кількісною оцінкою надійності (безвідмовності) є інтенсивність відмов або кількість відмов за одиницю часу або за одиницю пробігу. Отже, інтенсивність відмов –це величина обернено пропорційна до середнього напрацювання на відмову:
. (2)
Приклад. При
=50000
км інтенсивність відмов згідно виразу
(2) дорівнює
= 1/50000=2 10-5
відм./км.
Якщо знати інтенсивність відмов, то можна визначити приблизне число відмов nвідм. за тривалий період експлуатації l за формулою:
nвідм. = l. (3)
Приклад. Нехай інтенсивність відмов деталі автомобіля становить
= 2 10-5 відм./км, а ресурс за повний період експлуатації автомобіля l = 400 тис.км. Тоді число відмов даної деталі за повний термін служби автомобіля nвідм = 2 10-5 4 105 = 8 відмов.
Інтенсивність відмов – це кількісна оцінка безвідмовності деталей, що невідновлюються. Для деталей, що відновлюються (підлягають ремонту) використовують замість інтенсивності відмов параметр потоку відмов , який визначається так, як і , тобто за формулою (2).
Численні дослідження надійності ДТЗ свідчать, що інтенсивність відмов , як і параметр потоку відмов , не є величиною постійною, а такою, що залежить від віку деталей, вираженого пробігом з початку експлуатації l. Функція (l) зазвичай має такий характер, який показаний на рис. 1.
(l)
І ІІ ІІІ
l, тис .км
Рис.1. Залежність інтенсивності відмов (l) від пробігу з початку
експлуатації l: І – період припрацювання; ІІ – період нормальної, стійкої роботи; ІІІ – період старіння
Функція (l), яку зазвичай називають “-крива”, має три характерних періоди. У першому – періоді обкатки автомобіля, переважають випадкові, раптові відмови деталей; другий – період нормальної, сталої роботи автомобіля; третій – період його старіння, який характеризується зростанням кількості поступових відмов, обумовлених зношенням.
Визначити значення або за формулою (2) можна тільки у другому періоді, де = const. Для побудови всієї “-кривої” на ній виділяють елементарну дільницю l і приймають, що на цій дільниці (l)= const. Для оцінки інтенсивності відмов за даними випробувань користуються виразом:
, (4)
де
– число справних деталей ДТЗ, відповідно
на початку і в кінці ділянки l.
Наприклад, нехай на початку ділянки пробігу довжиною l =10 тис. км, при випробуваннях залишилося справних n(l) = 30 деталей, а в кінці ділянки – n (l+l)= 24 деталі. Тоді маємо:
відм./км.
2.3 Визначення імовірності безвідмовної роботи
Наступна кількісна оцінка надійності – імовірність безвідмовної роботи P(l) дорожнього транспортного засобу, агрегату, вузла або деталі на пробігу l. Для її визначення необхідно знати закон розподілу напрацювання на відмову та основні параметри цього закону. Імовірність безвідмовної роботи визначається за формулою:
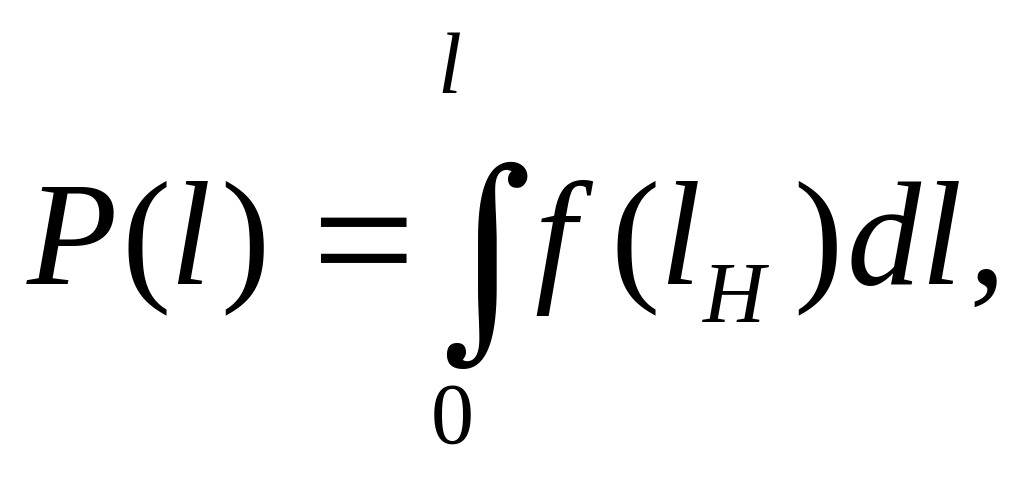(5)
де
щільність
імовірності напрацювання на відмову.
За нормальним
законом розподілення
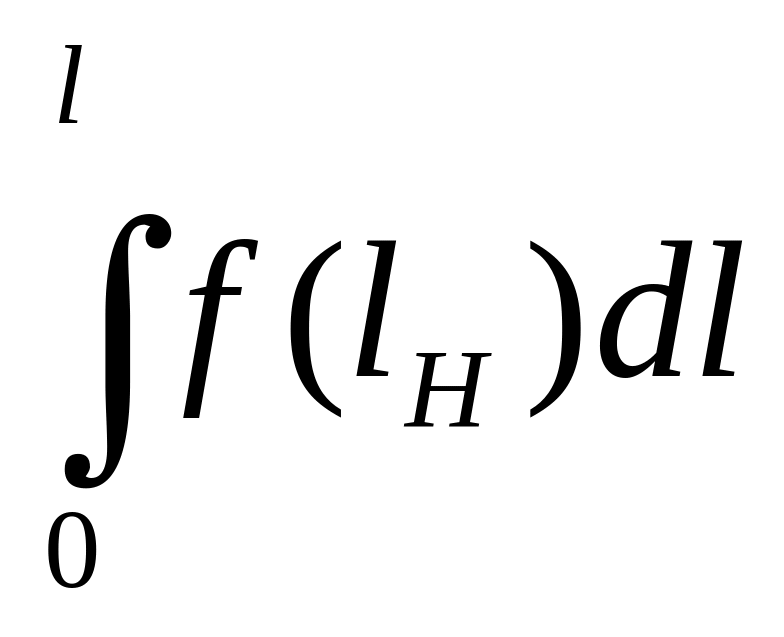визначається за допомогою функції
Лапласа Ф(х), значення якої наведені
у додатку 2.
Для нормального закону розподілення P(l) маємо:
. (6)
При використанні функції Лапласа необхідно мати на увазі наступні правила: Ф(-х)= -Ф(х); Ф(0)=0; Ф()=1.
Приклад. Нехай
напрацювання на відмову розподіляється
за нормальним законом з математичним
очікуванням
= 80 тис.км та середнім квадратичним
відхилення =
25 тис.км. Необхідно визначити імовірність
безвідмовної роботи деталі на протязі
перших l = 60 тис.км
пробігу автомобіля. Згідно
формули (6), з урахуванням правила знаків
Ф(-х)= -Ф(х) та значень, наведених у
додатку 2, маємо:
Р(60 тис.км) =
0,5 - 0,5 Ф
=0,5+0,5Ф(0,8)
= 0,5+0,5 0,5763
0,79.
Імовірність безвідмовної роботи Р(l) та імовірність відмови Q(l) величини, що доповнюють одна одну до одиниці:
P(l)+Q(l)=1 . (7)
Отже, якщо знати імовірність безвідмовної роботи, то можна визначити ймовірність відмови деталі за той же пробіг l:
Q(l)=1-P(l) . (8)
В даному випадку імовірність відмови становить:
Q(l)=1- 0,79=0,21.
Таким чином, якщо маємо значну кількість автомобілів однієї моделі, тоді з достатньою ступінню точності можна припустити, що після пробігу 30 тис.км, 21% розглядаємих деталей потребуватимуть заміни.
За експоненціальним законом розподілення імовірність безвідмовної роботи визначають за виразом:
P(l)=
=
.
(9)
Приклад. Нехай за умови попереднього прикладу, напрацювання на відмову деталі розподіляється за експоненціальним законом з математичним сподіванням = 80 тис.км. Необхідно визначити імовірність безвідмовної роботи на протязі перших l = 30 тис.км пробігу автомобіля. Тоді, згідно (9) маємо:
P
(30тис.км) =
= 0,50.
Використовуючи наведену методику, можна побудувати по точкам криву залежності ймовірності безвідмовної роботи деталі Р (l) від її строку служби l.
Приклад. Нехай, як у попередньому прикладі, напрацювання на відмову деталі розподіляється за експоненціальним законом з математичним очікуванням = 80 тис.км. Необхідно визначити ймовірність безвідмовної роботи для значень l, починаючи від 0 через кожні 40 тис.км. Тоді, згідно формули (9) отримаємо:
Побудована по визначеним величинам крива наведена на рис. 2.
P
(l)
1,00
0,75 P(l)
0,50
0,25
І І І І І І І І І І І І І І І І І І
40 120 200 280 360 440 520 600 680 l, тис. км
Рис.2. Залежність імовірності безвідмовної роботи
від пробігу з початку експлуатації