Примеры решения задач

Пример 1. Определить: 1) число N молекул воды, занимающей при температуре t=4 °С объем V=1мм³; 2) массу m₀ молекулы воды; 3) диаметр d молекулы воды, считая, что молекулы имеют форму шариков, соприкасающихся друг с другом.

Решение. 1. Число N молекул, содержащихся в теле неко­торой массы m, равно произведению постоянной Авогадро N_А на количество вещества :

N= N_А.

Так как =m/, где — моляр­ная масса, то

N=(m/) N_А.

Выразив в этой формуле массу как про­изведение плотности  на объем V, получим

N=(V/) N_А (1).

Все величины, кроме молярной массы воды, входящие в (1), известны: =1000кг/м³, N_А=6,0210²³ моль^-1.

Подставим значения величин в (1) и произведем вычисления;

N = [110³1 10^-9/1810^-3)] 6,0210²³ молекул = 3,3410¹⁹ молекул.

2. Массу одной молекулы воды найдем по формуле:

m₀=/ N_А

Произведя вычисления по этой формуле, получим

m₀=1810^-3/(6,0210²³) = 2,9910^-26, кг.

3. Будем считать, что молекулы плотно прилегают друг к другу, тогда на каждую молекулу диаметром d приходится объем (куби­ческая ячейка) V₀=d³. Отсюда

.

Объем V₀ найдем, разделив молярный объем V_ вещества на число молекул в моле, т. е. на постоянную Авогадро. Молярный объем равен отношению молярной массы к плот­ности вещества, т. е. V_=/. Поэтому можем записать, что

V₀=_=/(N_А).

Подставив полученное выражение V₀ в формулу (1), получим

Теперь подставим значения величин в полученную формулу и произведем вычисления:

d=3,l110¹⁰ м = 311 пм.

Пример 2. В баллоне объемом V=10 л находится гелий под давле­нием p₁ = l МПа при температуре T₁ = 300 К. После того как из баллона был израсходован гелий массой m=10 г, температура в баллоне понизилась до Т₂ = 290 К. Определить давление р₂ гелия, оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Клапейрона - Менделеева, применив его дважды к начальному и конечному состояниям газа. Для начального состояния уравнение имеет вид

P₁V=(m₁/)RT₁ (1)

а для конечного состояния –

P₂V=(m₂ /)RT₂ (2)

где m₁ и m₂ - массы гелия в начальном и конечном состояниях.

Выразим массы m₁ и m₂ гелия из уравнений (1) и (2):

m₁= P₁V  / RT₁ (3)

m₂= P₂V  / RT₂ (4)

Вычитая из (3) равенство (4), получим

m = m₁ – m₂ = (V  / R)( P₁/ T₁ – P₂/ T₂)

Отсюда найдем искомое давление:

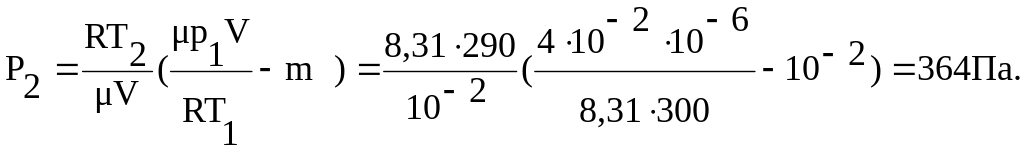
Пример 3. Какая часть молекул кислорода при 0⁰С обладает скоростью от 100м/c до 110 м/с?

Решение. Воспользуемся распределением молекул по относительным скоростям.

,

где u- относительная скорость. В нашем случае v=100 м/с и v=10 м/с. Наиболее вероятная скорость

.

Следовательно, u= v/v_в=100/376, u²=0,071, exp(-u²)= 0,93. Тогда,

Т.о., число молекул, скорости которых находятся в заданном интервале, составляют 4% от общего числа молекул.

Пример 4. Частицы гуммигута диаметром 0,310^-4см были взвешены в жидкости, плотность которой на 0,2 г/см³ меньше плотности частиц. Температура гуммигута 20⁰С. Найти по этим данным значение числа Авогадро, если в двух соседних слоях, расстояние между которыми 100 мкм, число частиц различается в два раза.

Решение. Проведем расчеты по формуле Больцмана.

тогда концентрация молекул на высоте h₁ определяется как

на высоте h₂

Отсюда, отношение концентраций определяется следующей зависимостью,

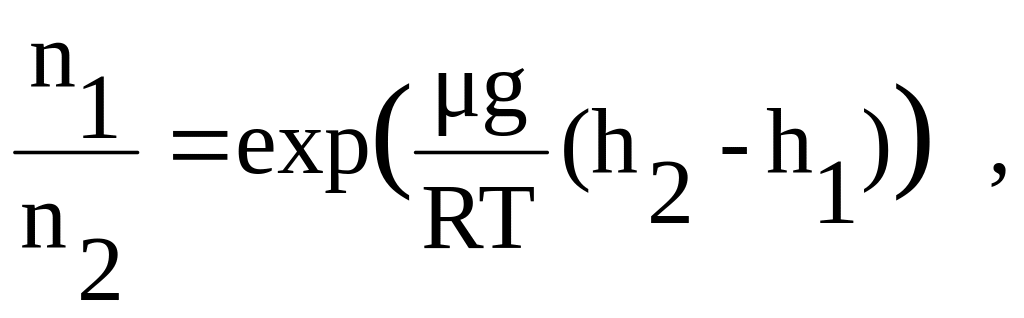или

Т.к. масса частицы определяется выражением m₀ = /N_A, то можно записать:

Из этого выражения, учитывая поправку на силу Архимеда, получим

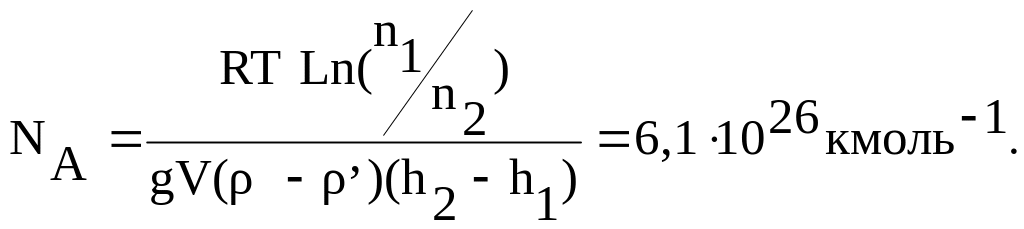
Где  и ^, - соответственно плотность гуммигута и жидкости.

Пример 5. Вычислить удельные теплоемкости С_v и C_p смеси неона и водорода. Массовые доли газов соответственно равны ₁=0,8 и ₂=0,2.

Решение. Удельную теплоемкость смеси при постоянном объеме С_V найдем из следующих рассуждений. Теплоту, необходи­мую для нагревания смеси на T, выразим двумя соотношениями:

Q = c_V(m₁ +m₂) T (1)

где c_V — удельная теплоемкость смеси m₁ — масса неона; m₂ — масса водорода, и

Q =( c_V1m₁ +c_V2m₂) T (2)

где c_V1 и c_V2 — удельные теплоемкости неона и водорода соответственно.

Приравняв правые части выражений (1) и (2) и разделив обе части полученного равенства на T, найдем

c_V (T₁ + T₂) = c_V1m₁ + c_V2m₂

откуда

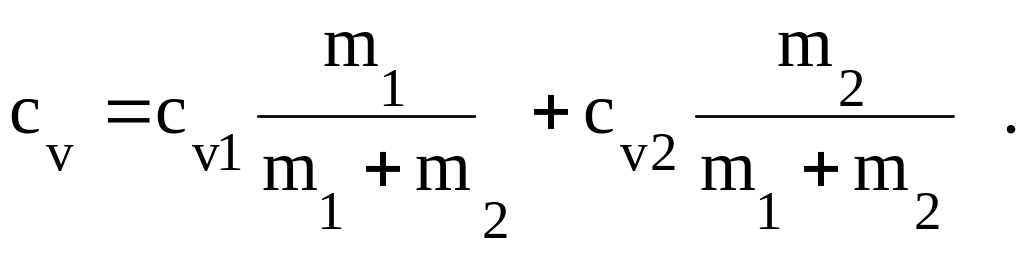
Отношения =m₁(m₁+m₂) и =m₂(m₁+m₂) выражают массовые доли соответственно неона и водорода. С учетом этих обозначений последняя формула примет вид

c_v=c_v1₁+c_v1₁.