4. Розв’язати рівняння

Практична робота 17

Дії над ймовірностями.

1. У ящику містяться 3 латунні (Л), 3 сталеві (С) і 1 бронзова (Б) деталь. Беруть 2 деталі. Визначити:

1. простір елементарних подій

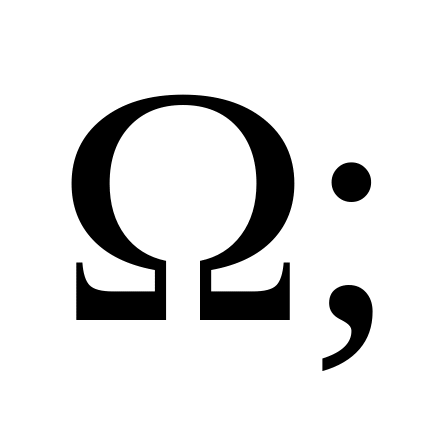
2. множину елементарних подій яка утворює з подіями 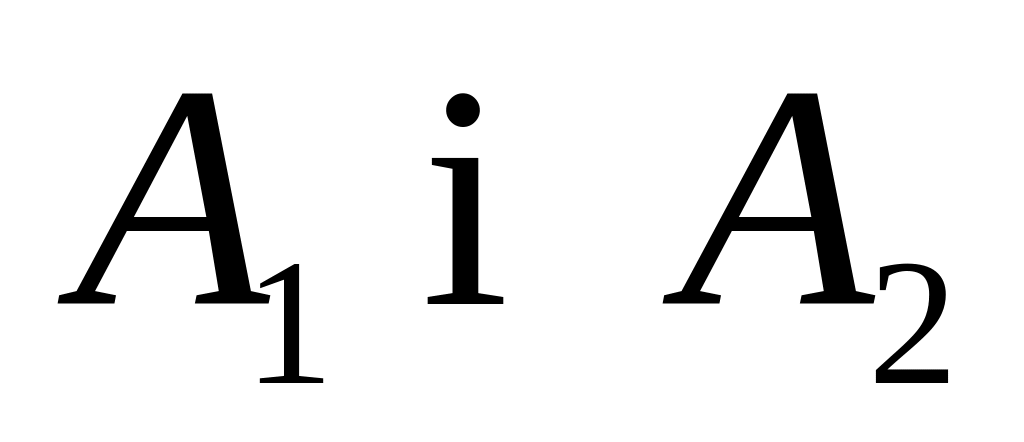повну групу, якщо — елементарні події, позначені згідно з матеріалом деталей.

2. У конверті 10 акцій, серед яких три фірми А. Навмання відібрано 4 акції. Яка імовірність того, що серед них буде одна акція фірми А?

3. До контролера надійшла партія однотипних виробів кількістю 20 шт. Серед них є п’ять бракованих, але про це йому невідомо. Контролер навмання бере чотири вироби для перевірки. Якщо всі відібрані вироби виявляться доброякісними, то партія пропускається. Знайти ймовірність того, що партія буде пропущена контролером.

4. Усередині круга радіусом R навмання вибирають точку. Знайти ймовірність того, що точка потрапить усередину:

1. вписаного у круг квадрата;

2. вписаного у круг правильного трикутника.

5. На колі взято будь-які три точки А, В, С. Знайти ймовірність того, що трикутник АВС гострокутний.

6. Механізм, що містить 4 однакові деталі, не працюватиме, якщо під час його складання буде взято 3 або більше деталей меншого розміру, ніж потрібно. У робітника залишилось 15 деталей, серед яких 6 меншого розміру. Знайти ймовірність того, що механізм працюватиме, якщо робітник братиме деталі навмання.

7. До банку надійшло 5000 пачок грошових знаків. Імовірність того, що пачку неправильно вкомплектовано, дорівнює 0,0004. Знайти ймовірність того, що серед одержаних пачок буде не більш як одна неправильно укомплектована.

8. У продавця канцтоварів у шухляді є 16 фломастерів українського виробництва, 8 — угорського і 14 — китайського. Знайти ймовірність того, що серед випадково вибраних п’ятнадцяти фломастерів тринадцять фломастерів виявляться імпортного виробництва.

ВАРІАНТ 10

Практична робота 1.

Дії над комплексними числами.

1. Виконати дії (12-і)-(-3+і)

2. Обчислити:і²⁵

3. Розв’язати рівняння: .

4. Знайти координати точки М, що зображує комплексне число

Практична робота 2

Дії над комплексними числами.

1. Виконати дії в алгебраїчній формі. Результат записати в тригонометричній та показникових формах .

Практична робота 3

Знаходження границь.

1. Функцію задано графіком, зображеним на рисунку:

Визначити при яких значеннях х функція від’ємна.

2. Визначіть інтервали знакосталості функції .

3.Знайти границю функції .

4. Знайти границю функції .

5. Знайти границю функції .

Практична робота 4

Перша та друга визначні границі.

1. Знайти границю функції .

2. Знайти границю функції .

3. Знайти точки розриву функції .

Практична робота 5

Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.

1. Задана функція у = f(x). Знайти у.

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

2. Знайти похідну другого порядку: .

3. Написати рівняння дотичної та нормалі до кривої у = х³ у точці М(1; 1).

Практична робота 6

Похідна. Схема повного дослідження і побудови графіка функції.

1. Визначити екстремуми функції: .

2. Знайти найбільше і найменше значення функції у заданому проміжку: .

3. Знайти точки перегину та інтервали опуклості і вгнутості графіку функції: .

4. Знайти асимптоти таких ліній: .

5. Провести повне дослідження функції і накреслити її графік: .

Практична робота 7

Невизначений інтеграл.

1. Розклавши підінтегральні функції за формулою , знайти такі інтеграли: а) ; б) .

2. Безпосереднім інтегруванням знайти інтеграл: .

3. Знайти інтеграл: .

4. Інтегруванням частинами знайти інтеграл:

5. Методом підстановки знайти інтеграл:

Практична робота 8

Визначений інтеграл.

1. Використовуючи метод підстановки, обчислити визначений інтеграл:

2. Інтегруванням частинами обчислити визначений інтеграл:

3. За допомогою визначеного інтегралу обчислити площу фігури, що обмежено лініями:

Практична робота 9

Дії на векторами. Дії над матрицями.

1. На осі ординат знайти точку, рівновіддалену від початку координат і прямої .

2. Знайти визначники третього порядку: .

3. Розкладаючи за другим стовпчиком, обчислити визначник: .

4. Обчислити вираз .

5. Знайти обернені до таких матриць: .

Практична робота 10

Дії над матрицями. Розв'язування систем лінійних рівнянь.

1. Розв’язати систему лінійних рівнянь за правилом Крамера. У разі залежності коефіцієнтів системи рівнянь від параметрів дослідити систему на сумісність.

2. Звести до матричного вигляду систему рівнянь і розв’язати методом оберненої матриці:

Практична робота 11

Система координат. Пряма та площина.

1. Знайти вершини трикутника, знаючи середини його сторін .

2. У трикутнику з вершинами проведені висота і медіана Написати рівняння сторони АС, медіани ВМ і висоти .

3. Скласти рівняння кола, що проходить через три задані точки: .

Практична робота 12

Загальне рівняння кривої другого порядку.

1. Як перетвориться рівняння кола , якщо перенести початок системи координат у точку .

2. Знайти кут між асимптотами гіперболи, у якої ексцентриситет дорівнює 2.

3. Визначити тип кривої другого порядку: .

4. Знайти рівняння площини, що проходить через точку і паралельна до площини .

Практична робота 13

Дії з рядами.

1. Запишіть три перші члени ряду, а також

2. Запишіть найпростішу формулу n-го члена ряду та перевірте виконання необхідної умови збіжності ряду:

3. Перевірте виконання необхідної умову збіжності ряду:

Практична робота 14

Дії з рядами.

1. Дослідити збіжність ряду, користуючись безпосередньо означенням збіжності ряду. Знайти суму ряду:

2. За допомогою ознак порівняння дослідити збіжність ряду:

3. Дослідити збіжність ряду за допомогою ознаки Даламбера:

Практична робота 15

Розв'язування диференційних рівнянь першого порядку

1. Розв’язати диференційне рівняння першого порядку:

2. Знайти частинні розв’язки диференціального рівнянь, що задовольняють задані початкові умови: при

3. Знайти частинні розв’язки диференціального рівнянь: при

Практична робота 16

Розв'язування однорідних диференційних рівнянь

1. Знайти частинний розв’язок однорідного диференціального рівняння: при

2. Розв’язати диференціальне рівняння в повних диференціалах:

3. Розв’язати диференціальне рівняння першого порядку:

4. Розв’язати рівняння при

Практична робота 17

Дії над ймовірностями.

1. У ящику містяться 3 латунні (Л), 3 сталеві (С) і 1 бронзова (Б) деталь. Беруть 2 деталі. Визначити:

3. простір елементарних подій

4. множину елементарних подій яка утворює з подіями повну групу, якщо — елементарні події, позначені згідно з матеріалом деталей.

2. Партія складається з 20 виробів, з яких 8 виробів 1-го сорту, 6—2-го, 2—3-го сорту, а решта — браковані. Навмання беруть 4 вироби. Знайти ймовірність того, що серед них виявилося 2 вироби 1-го сорту, 1—2-го сорту і 1 бракований.

3. Пасажир забув дві останні цифри коду комірки автоматичної камери схову, де він залишив речі. Знайти ймовірність того, що після першого набору коду із двома останніми навмання набраними цифрами комірка відчиниться, а також імовірність цієї ж події у випадку, коли пасажир пам’ятає, що ці цифри різні.

4. У контейнері є 20 деталей, серед яких 8 нестандартних. Знайти ймовірність того, що число нестандартних деталей серед п’яти навмання взятих деталей виявиться рівним: а) 0; б) 2; в) 5.

5. На колі взято будь-які три точки А, В, С. Знайти ймовірність того, що трикутник АВС гострокутний.

6. Механізм, що містить 4 однакові деталі, не працюватиме, якщо під час його складання буде взято 3 або більше деталей меншого розміру, ніж потрібно. У робітника залишилось 15 деталей, серед яких 6 меншого розміру. Знайти ймовірність того, що механізм працюватиме, якщо робітник братиме деталі навмання.

7. До банку надійшло 5000 пачок грошових знаків. Імовірність того, що пачку неправильно вкомплектовано, дорівнює 0,0004. Знайти ймовірність того, що серед одержаних пачок буде не більш як одна неправильно укомплектована.

8. Гросмейстер демонструє сеанс одночасної гри на 14 дошках з аматорами, серед яких 8 надають перевагу захисту Альохіна, 3 — «Каро-Кан» і троє — індійській обороні. Яка ймовірність того, що на перших п’яти шахівницях буде розіграно захист Альохіна?

ВАРІАНТ 11

Практична робота 1.

Дії над комплексними числами.

1. Виконати дії і(1+і)

2. В якій чверті розміщене комплексне число 4-і

3. Розв’язати рівняння:

4. Знайти число спряжене з числом

Практична робота 2

Дії над комплексними числами.

1. Виконати дії в алгебраїчній формі. Результат записати в тригонометричній та показникових формах .

Практична робота 3

Знаходження границь.

1. Функцію задано графіком, зображеним на рисунку:

Визначити при яких значеннях х функція спадає.

2. Знайти область визначення функції .

3.Знайти границю функції .

4. Знайти границю функції .

5. Знайти границю функції .

Практична робота 4

Перша та друга визначні границі.

1. Знайти границю функції .

2. Знайти границю функції .

3. Знайти точки розриву функції .

Практична робота 5

Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.

1. Задана функція у = f(x). Знайти у.

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

2. Знайти похідну другого порядку: .

3. Нехай — рівняння вільного руху тіла, g — прискорення його вільного падіння. Знайти миттєву швидкість тіла в будь-який момент часу; у момент часу t = 2 c.

Практична робота 6

Похідна. Схема повного дослідження і побудови графіка функції.

1. Визначити екстремуми функції: .

2. Знайти найбільше і найменше значення функції у заданому проміжку: .

3. Знайти точки перегину та інтервали опуклості і вгнутості графіку функції: .

4. Знайти асимптоти таких ліній: .

5. Провести повне дослідження функції і накреслити її графік: .

Практична робота 7

Невизначений інтеграл.

1. Розклавши підінтегральні функції за формулою , знайти такі інтеграли: а) ; б) .

2. Безпосереднім інтегруванням знайти інтеграл: .

3. Знайти інтеграл: .

4. Інтегруванням частинами знайти інтеграл:

5. Методом підстановки знайти інтеграл:

Практична робота 8

Визначений інтеграл.

1. Використовуючи метод підстановки, обчислити визначений інтеграл:

2. Інтегруванням частинами обчислити визначений інтеграл:

3. За допомогою визначеного інтегралу обчислити площу фігури, що обмежено лініями:

Практична робота 9

Дії на векторами. Дії над матрицями.

1. Знайти відстані точок від прямої .

2. Знайти визначники третього порядку: .

3. Обчислити визначник .

4. Обчислити вираз .

5. Знайти обернені до таких матриць: .

Практична робота 10

Дії над матрицями. Розв'язування систем лінійних рівнянь.

1. Розв’язати систему лінійних рівнянь за правилом Крамера. У разі залежності коефіцієнтів системи рівнянь від параметрів дослідити систему на сумісність.

2. Звести до матричного вигляду систему рівнянь і розв’язати методом оберненої матриці:

Практична робота 11

Система координат. Пряма та площина.

1. Дано вершини трикутника . Визначити довжини його сторін.

2. Написати рівняння прямої, що проходить через початок системи координат і: 1) паралельна прямій ; 2) перпендику­лярна прямій ; 3) утворює кут, що дорівнює 45, з прямою ; 4) нахилена під кутом в 60 до прямої .

3. Знайти відстані точок від прямої .

Практична робота 12

Загальне рівняння кривої другого порядку.

1. Звести до канонічного вигляду рівняння кола .

2. Скласти канонічне рівняння еліпса, коли відомо, що півосі його дорівнюють 4 і 2 одиницям.

3. Визначити тип кривої другого порядку: .

4. Написати рівняння площини, що проходить через точки ; М₃(1, –2, 1).

Практична робота 13

Дії з рядами.

1. Запишіть три перші члени ряду, а також

2. Запишіть найпростішу формулу n-го члена ряду та перевірте виконання необхідної умови збіжності ряду:

3. Перевірте виконання необхідної умову збіжності ряду:

Практична робота 14

Дії з рядами.

1. Дослідити збіжність ряду, користуючись безпосередньо означенням збіжності ряду. Знайти суму ряду:

2. За допомогою ознак порівняння дослідити збіжність ряду:

3. Дослідити збіжність ряду за допомогою ознаки Даламбера:

Практична робота 15

Розв'язування диференційних рівнянь першого порядку

1. Розв’язати диференційне рівняння першого порядку:

2. Знайти частинні розв’язки диференціального рівнянь, що задовольняють задані початкові умови: при

3. Знайти частинні розв’язки диференціального рівнянь: , при .

Практична робота 16

Розв'язування однорідних диференційних рівнянь

1. Знайти частинний розв’язок однорідного диференціального рівняння: при

2. Розв’язати диференціальне рівняння в повних диференціалах:

3. Розв’язати диференціальне рівняння першого порядку: