4. Розв’язати рівняння
Практична робота 17
Дії над ймовірностями.
1. Із ящика, в якому є бронзові, мідні, латунні та сталеві деталі, беруть одну деталь. Події означають відповідно, що взята деталь бронзова, латунна, мідна, сталева. Визначити подію
2. Партія складається з 20 виробів, з яких 8 виробів 1-го сорту, 6—2-го, 2—3-го сорту, а решта — браковані. Навмання беруть 4 вироби. Знайти ймовірність того, що серед них виявилося 2 вироби 1-го сорту, 1—2-го сорту і 1 бракований.
3. До контролера надійшла партія однотипних виробів кількістю 20 шт. Серед них є п’ять бракованих, але про це йому невідомо. Контролер навмання бере чотири вироби для перевірки. Якщо всі відібрані вироби виявляться доброякісними, то партія пропускається. Знайти ймовірність того, що партія буде пропущена контролером.
4. У контейнері є 20 деталей, серед яких 8 нестандартних. Знайти ймовірність того, що число нестандартних деталей серед п’яти навмання взятих деталей виявиться рівним: а) 0; б) 2; в) 5.
5. У коло радіуса 10 кидають точку. Знайти ймовірність того, що відстань від точки до центра кола не перевищує 4.
6. Маємо дві партії деталей. У першій партії сім придатних і три браковані деталі. У другій — 10 придатних і чотири браковані. Із кожної партії навмання беруть по одній деталі. Знайти ймовірність такої події:
обидві деталі придатні;
обидві деталі браковані;
одна деталь придатна, а друга бракована.
7. Частка 2-го сорту деякої масової продукції в середньому становить 20 %. Навмання взято 100 примірників цієї продукції. Яка кількість виробів 2-го сорту в утвореній групі найімовірніша і яка ймовірність того, що в цій групі буде саме така кількість виробів 2-го сорту?
8. Частка 1-го сорту в деякій продукції в середньому становить 80 %. Скільки примірників цієї продукції треба взяти, щоб з імовірністю 0,9 можна було стверджувати, що в партії буде не менш як 75 примірників 1-го сорту?
ВАРІАНТ 7
Практична робота 1.
Дії над комплексними числами.
1.
Виконати дії
2. В якій чверті розміщене комплексне число 4-і
3.
Розв’язати рівняння:
.
4. Знайти число спряжене з числом
Практична робота 2
Дії над комплексними числами.
1.
Виконати дії в алгебраїчній формі.
Результат записати в тригонометричній
та показникових формах
.
Практична робота 3
Знаходження границь.
1. Функцію задано графіком, зображеним на рисунку:
Визначити при яких значеннях х функція спадає.
2. Знайти область визначення функції .
3.Знайти границю функції .
4.
Знайти границю функції
.
5. Знайти границю функції .
Практична робота 4
Перша та друга визначні границі.
1.
Знайти границю функції
.
2.
Знайти границю функції
.
3. Знайти
точки розриву функції
.
Практична робота 5
Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.
1. Задана функція у = f(x). Знайти у.
1)
;
2) ;
3)
;
4) ;
5) ;
6) ;
7)
;
8) ;
2. Знайти похідну другого порядку: .
3. Нехай — рівняння вільного руху тіла, g — прискорення його вільного падіння. Знайти миттєву швидкість тіла в будь-який момент часу; у момент часу t = 2 c.
Практична робота 6
Похідна. Схема повного дослідження і побудови графіка функції.
1. Визначити екстремуми функції: .
2. Знайти найбільше і найменше значення функції у заданому проміжку: .
3. Знайти точки перегину та інтервали опуклості і вгнутості графіку функції: .
4. Знайти асимптоти таких ліній: .
5. Провести повне дослідження функції і накреслити її графік: .
Практична робота 7
Невизначений інтеграл.
1. Розклавши підінтегральні функції за формулою , знайти такі інтеграли: а) ; б) .
2. Безпосереднім інтегруванням знайти інтеграл: .
3.
Знайти інтеграл:
.
4. Інтегруванням частинами знайти інтеграл:
5. Методом підстановки знайти інтеграл:
Практична робота 8
Визначений інтеграл.
1. Використовуючи метод підстановки, обчислити визначений інтеграл:
2. Інтегруванням частинами обчислити визначений інтеграл:
3. За
допомогою визначеного інтегралу
обчислити площу фігури, що обмежено
лініями:
Практична робота 9
Дії на векторами. Дії над матрицями.
1.Знайти
відстань між прямими
і
.
2.
Знайти визначники третього порядку: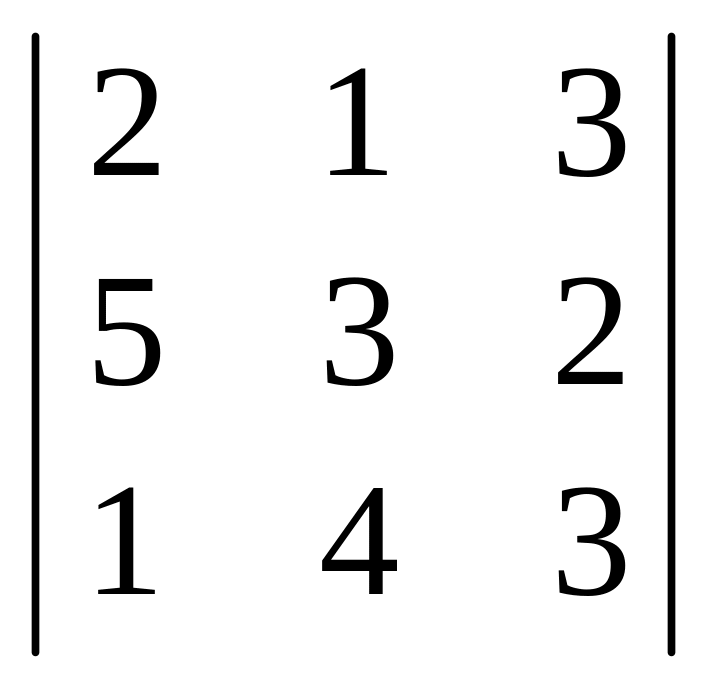
.
3. Обчислити визначник .
4.
Знайти добутки матриць: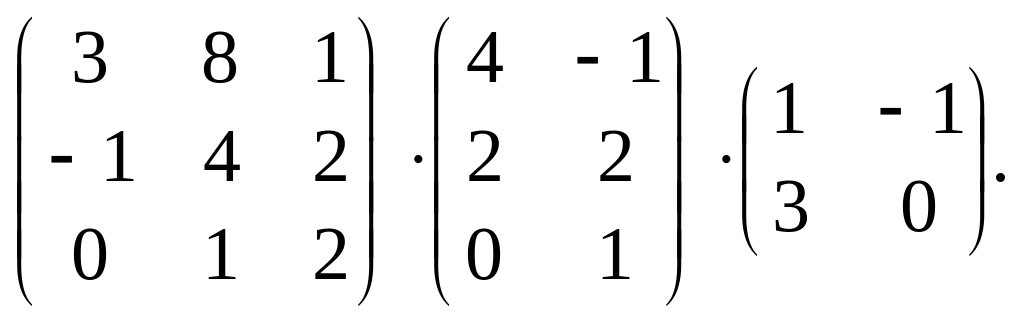
5. Знайти обернені до таких матриць: .
Практична робота 10
Дії над матрицями. Розв'язування систем лінійних рівнянь.
1. Розв’язати систему лінійних рівнянь за правилом Крамера. У разі залежності коефіцієнтів системи рівнянь від параметрів дослідити систему на сумісність.
2. Звести до матричного вигляду систему рівнянь і розв’язати методом оберненої матриці:
Практична робота 11
Система координат. Пряма та площина.
1. На осі ординат знайти точки, що віддалені від точки на відстані 5 одиниць.
2. У трикутнику з вершинами проведені висота і медіана Написати рівняння сторони АС, медіани ВМ і висоти .
3. Знайти відстані точок від прямої .
Практична робота 12
Загальне рівняння кривої другого порядку.
1. Звести до канонічного вигляду рівняння кола .
2. Дано рівняння еліпса: . Обчислити довжини осей, координати фокусів та його ексцентриситет.
3.
Визначити тип кривої другого порядку:
.
4. Написати рівняння площини, що проходить через дві паралельні прямі: і .
Практична робота 13
Дії з рядами.
1. Запишіть три перші члени ряду, а також
2. Запишіть
найпростішу формулу n-го
члена ряду та перевірте виконання
необхідної умови збіжності ряду:
3.
Перевірте виконання необхідної умову
збіжності ряду:
Практична робота 14
Дії з рядами.
1. Дослідити збіжність ряду, користуючись безпосередньо означенням збіжності ряду. Знайти суму ряду:
2.
За допомогою ознак порівняння дослідити
збіжність ряду:
3.
Дослідити збіжність ряду за допомогою
ознаки Даламбера:
Практична робота 15
Розв'язування диференційних рівнянь першого порядку
1. Розв’язати диференційне рівняння першого порядку:
2. Знайти частинні розв’язки диференціального рівнянь, що задовольняють задані початкові умови: при
3. Знайти частинні розв’язки диференціального рівнянь: при
Практична робота 16
Розв'язування однорідних диференційних рівнянь
1. Знайти загальний розв’язок однорідного диференціального рівняння:
2. Розв’язати диференціальне рівняння в повних диференціалах:
3. Розв’язати диференціальне рівняння першого порядку: