4. Розв’язати рівняння

Практична робота 17

Дії над ймовірностями.

1. Із ящика, в якому є бронзові, мідні, латунні та сталеві деталі, беруть одну деталь. Події означають відповідно, що взята деталь бронзова, латунна, мідна, сталева. Визначити подію

2. У конверті 10 акцій, серед яких три фірми А. Навмання відібрано 4 акції. Яка імовірність того, що серед них буде одна акція фірми А?

3. Академічній групі, в якій 12 дівчат та 18 юнаків, запропоновано придбати 10 акцій банку «Надра». Знайти ймовірність того, що власниками акцій стануть 4 юнаки та 3 дівчини, якщо розігрування здійснюється випадковим чином.

4. Серед 18 телевізорів, що продаються, 6 вимагають додаткового регулювання. Знайти ймовірність того, що з п’яти куплених телевізорів два потребуватимуть додаткового регулювання.

5. У коло радіуса 10 кидають точку. Знайти ймовірність того, що відстань від точки до центра кола не перевищує 4.

6. Маємо дві партії деталей. У першій партії сім придатних і три браковані деталі. У другій — 10 придатних і чотири браковані. Із кожної партії навмання беруть по одній деталі. Знайти ймовірність такої події:

7. обидві деталі придатні;

8. обидві деталі браковані;

9. одна деталь придатна, а друга бракована.

7. На кожні 30 штампованих виробів у середньому припадає 6 виробів з дефектом. Знайти ймовірність того, що з 5 навмання взятих виробів 3 виявляться без дефекту.

8. Гросмейстер демонструє сеанс одночасної гри на 14 дошках з аматорами, серед яких 8 надають перевагу захисту Альохіна, 3 — «Каро-Кан» і троє — індійській обороні. Яка ймовірність того, що на перших п’яти шахівницях буде розіграно захист Альохіна?

ВАРІАНТ 6

Практична робота 1.

Дії над комплексними числами.

1. Виконати дії (2+3і)+(-4+і).

2. В якій чверті розміщене комплексне число -3+і

3. Розв’язати рівняння:

4. Знайти координати точки М, що зображує комплексне число

Практична робота 2

Дії над комплексними числами.

1. Виконати дії в алгебраїчній формі. Результат записати в тригонометричній та показникових формах .

Практична робота 3

Знаходження границь.

1. Функцію задано графіком, зображеним на рисунку:

Визначити при яких значеннях х функція спадає.

2. Знайти область визначення функції .

3.Знайти границю функції .

4. Знайти границю функції .

5. Знайти границю функції .

Практична робота 4

Перша та друга визначні границі.

1. Знайти границю функції .

2. Знайти границю функції .

3. Знайти точки розриву функції .

Практична робота 5

Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.

1. Задана функція у = f(x). Знайти у.

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

2. Знайти похідну другого порядку: .

3. Знайти тангенси кутів нахилу дотичної до кривої у = х2 у точках М1(½; ¼), М2(–1; 1).

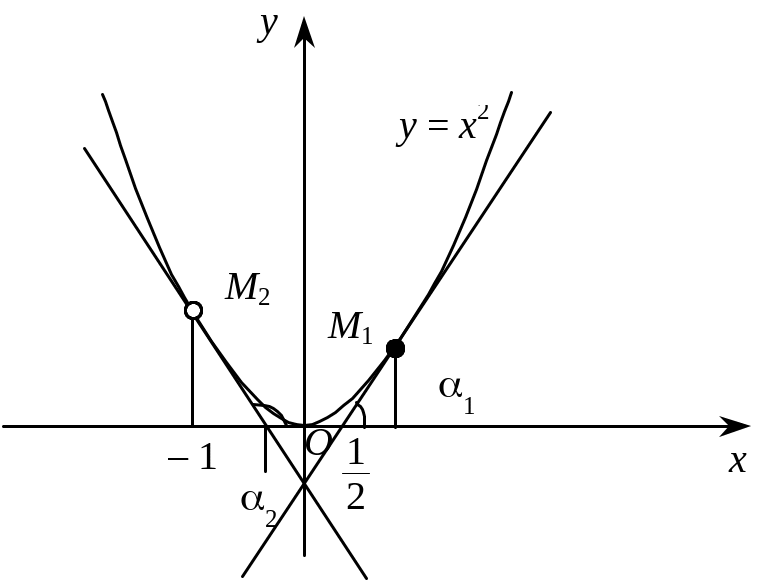
Практична робота 6

Похідна. Схема повного дослідження і побудови графіка функції.

1. Визначити екстремуми функції: .

2. Знайти найбільше і найменше значення функції у заданому проміжку: .

3. Знайти точки перегину та інтервали опуклості і вгнутості графіку функції: .

4. Знайти асимптоти таких ліній: .

5. Провести повне дослідження функції і накреслити її графік: .

Практична робота 7

Невизначений інтеграл.

1. Розклавши підінтегральні функції за формулою , знайти такі інтеграли: а) ; б) .

2. Безпосереднім інтегруванням знайти інтеграл: .

3. Знайти інтеграл: .

4. Інтегруванням частинами знайти інтеграл:

5. Методом підстановки знайти інтеграл:

Практична робота 8

Визначений інтеграл.

1. Використовуючи метод підстановки, обчислити визначений інтеграл:

2. Інтегруванням частинами обчислити визначений інтеграл:

3. За допомогою визначеного інтегралу обчислити площу фігури, що обмежено лініями:

Практична робота 9

Дії на векторами. Дії над матрицями.

1. Знайти відстані точок від прямої .

2. Знайти визначники другого порядку: .

3. Розкладаючи за другим стовпчиком, обчислити визначник: .

4. Знайти добутки матриць: .

5. Знайти обернені до таких матриць: .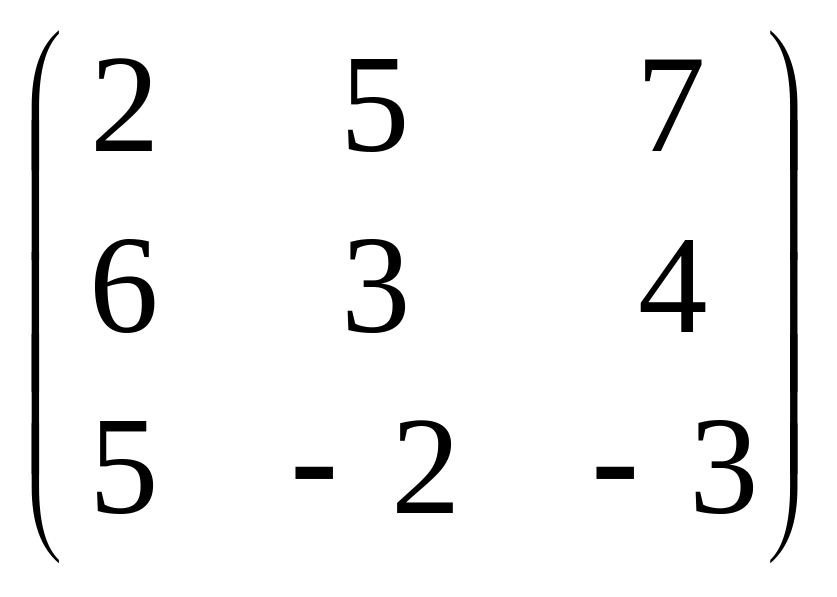

Практична робота 10

Дії над матрицями. Розв'язування систем лінійних рівнянь.

1. Розв’язати систему лінійних рівнянь за правилом Крамера. У разі залежності коефіцієнтів системи рівнянь від параметрів дослідити систему на сумісність.

2. Звести до матричного вигляду систему рівнянь і розв’язати методом оберненої матриці:

Практична робота 11

Система координат. Пряма та площина.

1. Дано вершини трикутника . Визначити довжини його сторін.

2. У трикутнику з вершинами проведені висота і медіана Написати рівняння сторони АС, медіани ВМ і висоти .

3. Скласти рівняння кола, що проходить через три задані точки: .

Практична робота 12

Загальне рівняння кривої другого порядку.

1. Звести до канонічного вигляду рівняння кола

2. Скласти канонічне рівняння еліпса, коли відомо, що велика піввісь дорівнює 10 одиницям, а ексцентриситет .

3. Визначити тип кривої другого порядку: .

4. Написати рівняння площини, що проходить через точки ; М₃(1, –2, 1).

Практична робота 13

Дії з рядами.

1. Запишіть три перші члени ряду, а також

2. Запишіть найпростішу формулу n-го члена ряду та перевірте виконання необхідної умови збіжності ряду:

3. Перевірте виконання необхідної умову збіжності ряду:

Практична робота 14

Дії з рядами.

1. Дослідити збіжність ряду, користуючись безпосередньо означенням збіжності ряду. Знайти суму ряду:

2. За допомогою ознак порівняння дослідити збіжність ряду:

3. Дослідити збіжність ряду за допомогою ознаки Даламбера:

Практична робота 15

Розв'язування диференційних рівнянь першого порядку

1. Розв’язати диференційне рівняння першого порядку:

2. Знайти частинні розв’язки диференціального рівнянь, що задовольняють задані початкові умови: при

3. Знайти частинні розв’язки диференціального рівнянь: , при .

Практична робота 16

Розв'язування однорідних диференційних рівнянь

1. Знайти частинний розв’язок однорідного диференціального рівняння: при

2. Розв’язати диференціальне рівняння в повних диференціалах:

3. Розв’язати диференціальне рівняння першого порядку: