ВАРІАНТ 1
Практична робота 1.
Дії над комплексними числами.
1.
Виконати дії
.
2. Побудувати на числовій площині та знайти модуль комплексного числа (-2+5і).
3.
Розв’язати рівняння:
.
4.
Знайти число спряжене з числом
Практична робота 2
Дії над комплексними числами.
1.
Виконати
дії в алгебраїчній формі. Результат
записати в тригонометричній та
показникових формах
.
Практична робота 3
Знаходження границь.
1. Функцію задано графіком, зображеним на рисунку:
Визначити при яких значеннях х функція додатна.
2.
Знайти область визначення функції
.
3.Знайти
границю функції
.
4.
Знайти границю функції
.
5.
Знайти границю функції
.
Практична робота 4
Перша та друга визначні границі.
1.
Знайти границю функції
.
2.
Знайти границю функції
.
3. Знайти
точки розриву функції
.
Практична робота 5
Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.
1. Задана функція у = f(x). Знайти у.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
2.
Знайти похідну другого порядку:
.
3.
Нехай
— рівняння вільного руху тіла, g —
прискорення його вільного падіння.
Знайти миттєву швидкість тіла в будь-який
момент часу; у момент часу t = 2 c.
Практична робота 6
Похідна. Схема повного дослідження і побудови графіка функції.
1.
Визначити екстремуми функції:
.
2.
Знайти найбільше і найменше значення
функції у заданому проміжку:
.
3.
Знайти точки перегину та інтервали
опуклості і вгнутості графіку функції:
.
4.
Знайти асимптоти таких ліній:
.
5.
Провести повне дослідження функції і
накреслити її графік:
.
Практична робота 7
Невизначений інтеграл.
1. Розклавши
підінтегральні функції за формулою
,
знайти
такі інтеграли: а)
;
б)
.
2.
Безпосереднім інтегруванням знайти
інтеграл:
.
3.
Знайти інтеграл:
.
4.
Інтегруванням частинами знайти інтеграл:
5.
Методом підстановки знайти інтеграл:
Практична робота 8
Визначений інтеграл.
1.
Використовуючи метод підстановки,
обчислити визначений інтеграл:
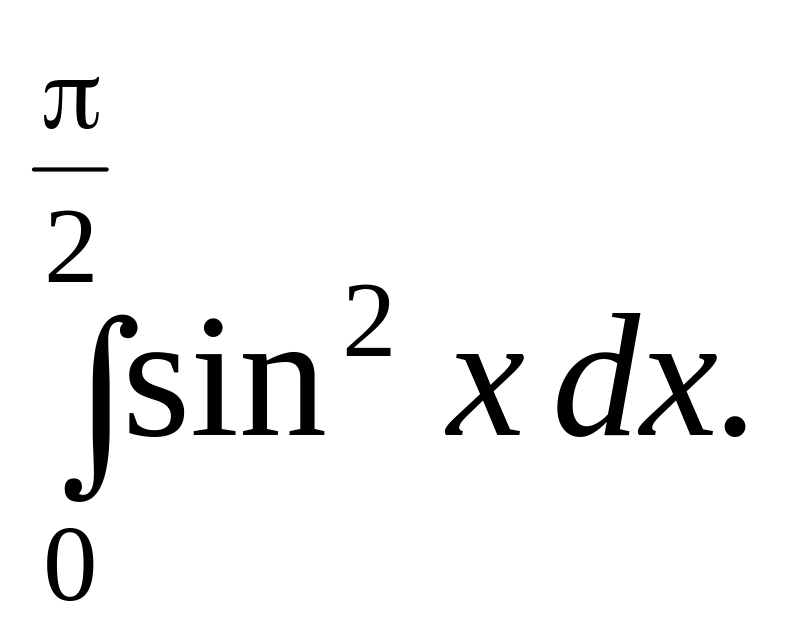
2.
Інтегруванням частинами обчислити
визначений інтеграл:
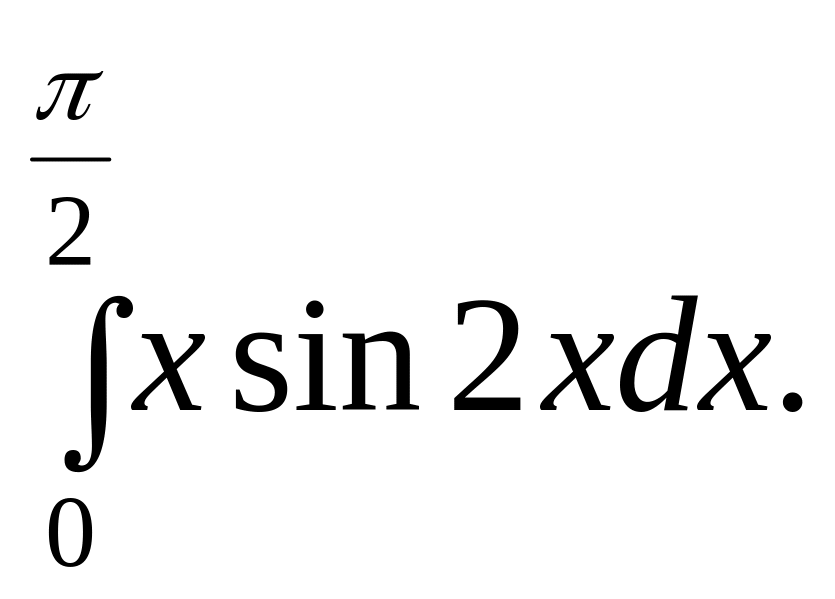
3. За
допомогою визначеного інтегралу
обчислити площу фігури, що обмежено
лініями:
Практична робота 9
Дії на векторами. Дії над матрицями.
1.
Дано три вершини паралелограма:
Знайти координати четвертої вершини
,
що протилежна вершині В.
2. Знайти
визначники третього порядку: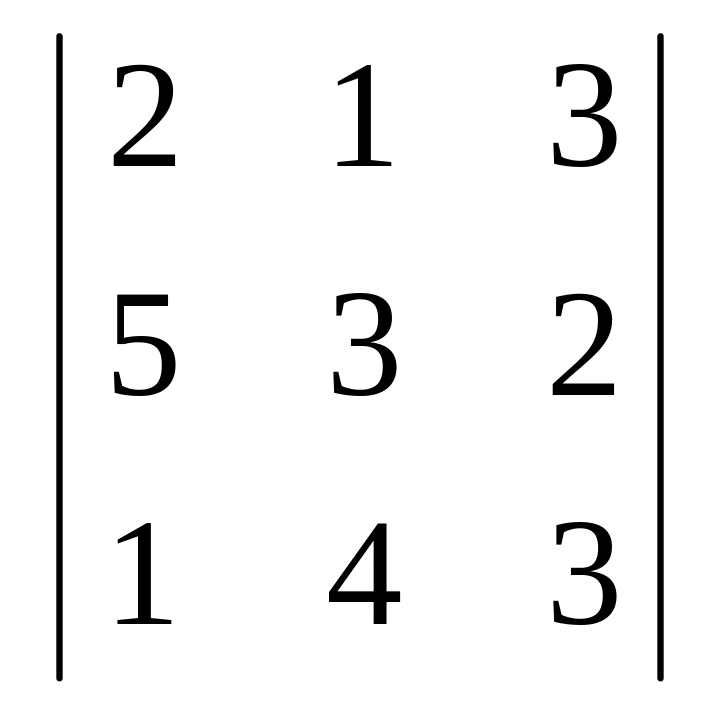
;
3.
Розкладаючи за третім рядком, обчислити
визначник:
.
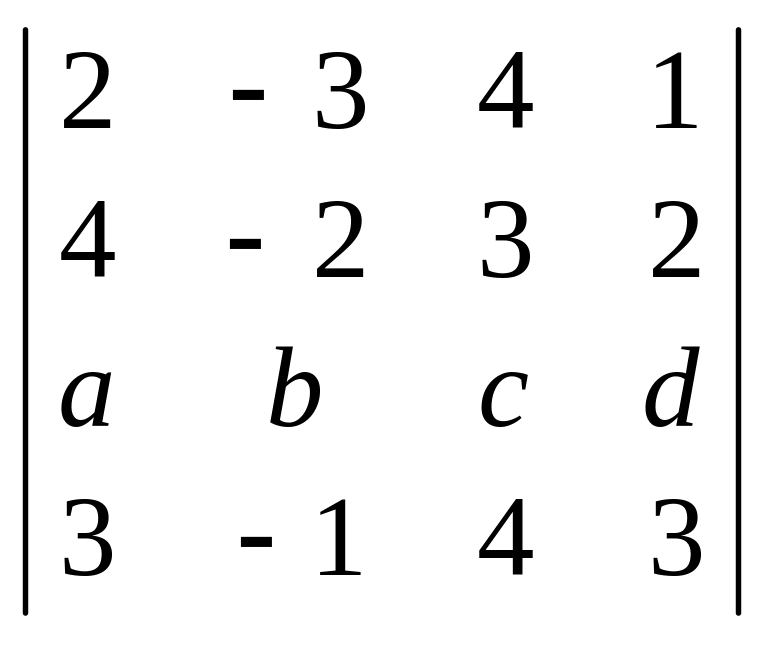4.
Знайти добутки матриць:
.
5.
Знайти обернені до таких матриць:
.
Практична робота 10
Дії над матрицями. Розв'язування систем лінійних рівнянь.
1.
Розв’язати систему лінійних рівнянь
за правилом Крамера. У разі залежності
коефіцієнтів системи рівнянь від
параметрів дослідити систему на
сумісність.
2.
Звести до матричного вигляду систему
рівнянь і розв’язати методом оберненої
матриці:
Практична робота 11
Система координат. Пряма та площина.
1.
Дано вершини трикутника
.
Визначити довжини його сторін.
2.
Знайти
точку перетину медіан трикутника, якщо
координатами його вершин є:
і
.
3.
Знайти відстані точок
від прямої
.
Практична робота 12
Загальне рівняння кривої другого порядку.
1.
Звести до канонічного вигляду рівняння
кола
.
2.
Дано рівняння еліпса:
.
Обчислити довжини осей, координати
фокусів та його ексцентриситет.
3.
Визначити тип кривої другого порядку:
.
4.
Написати рівняння площини, що проходить
через точки
;
М3(1,
–2, 1).
Практична робота 13
Дії з рядами.
1. Запишіть
три перші члени ряду, а також
2. Запишіть
найпростішу формулу n-го
члена ряду та перевірте виконання
необхідної умови збіжності ряду:
3.
Перевірте виконання необхідної умову
збіжності ряду:
Практична робота 14
Дії з рядами.
1.
Дослідити збіжність ряду, користуючись
безпосередньо означенням збіжності
ряду. Знайти суму ряду:
2.
За допомогою ознак порівняння дослідити
збіжність ряду:
3.
Дослідити збіжність ряду за допомогою
ознаки Даламбера:
Практична робота 15
Розв'язування диференційних рівнянь першого порядку
1.
Розв’язати диференційне рівняння
першого порядку:
2. Знайти
частинні розв’язки диференціального
рівнянь, що задовольняють задані
початкові умови:
при
.
(Задача Коші.)
3. Знайти
частинні розв’язки диференціального
рівнянь:
при
Практична робота 16
Розв'язування однорідних диференційних рівнянь
1.
Знайти частинний розв’язок однорідного
диференціального рівняння:
при
2.
Розв’язати диференціальне рівняння в
повних диференціалах:
3.
Розв’язати диференціальне рівняння
першого порядку:
4. Розв’язати рівняння
Практична робота 17
Дії над ймовірностями.
1. Партія складається зі стандартних і нестандартних деталей, які ретельно перемішані. З неї навмання беруть дві деталі. Визначити:
простір елементарних подій;
множини елементарних подій для таких подій:
а) 
— поява однієї стандартної і однієї
нестандартної деталей;
б) 
— поява не менш як однієї стандартної
деталі;
в) 
— поява не більш як однієї стандартної
деталі.
2. До ліфта дев’ятиповерхового будинку на 1-му поверсі зайшло троє пасажирів. Кожен із них з однаковою ймовірністю виходить на будь-якому з поверхів, починаючи з 2-го. Знайти ймовірність того, що всі пасажири:
вийдуть на 5-му поверсі;
вийдуть одночасно на одному з поверхів;
вийдуть на різних поверхах.
3. Академічній групі, в якій 12 дівчат та 18 юнаків, запропоновано придбати 10 акцій банку «Надра». Знайти ймовірність того, що власниками акцій стануть 4 юнаки та 3 дівчини, якщо розігрування здійснюється випадковим чином.
4. Стержень
завдовжки
розрубують на дві частини. Знайти
ймовірність того, що менша з частин, на
які він поділяється, має довжину не менш
як
5. Від аеровокзалу відправились два автобуси. Імовірність своєчасного прибуття кожного з них дорівнює 0,92. Знайти ймовірність такої події:
А — обидва автобуси прибудуть своєчасно;
В — обидва автобуси запізняться;
С — тільки один автобус прибуде своєчасно.
6. Для посіву пшениці заготовлено насіння, серед якого 95 % 1-го сорту, 3 % 2-го та 2 % 3-го сорту. Імовірність того, що з насінини виросте колосок, в якому не менш ніж 50 зерен, для 1-го сорту насіння становить 0,5, для 2-го сорту — 0,2, для 3-го — 0,1. Знайти ймовірність того, що навмання взятий колосок у разі такого посіву матиме не менш як 50 зерен.
7. Імовірність виграшу облігації за весь період позики становить 0,6. Куплено 5 облігацій. Знайти ймовірність такої події:
виграють дві облігації;
виграш випаде принаймні на одну облігацію;
виграють не більш як дві облігації.
8. Частка 1-го сорту в деякій продукції в середньому становить 80 %. Скільки примірників цієї продукції треба взяти, щоб з імовірністю 0,9 можна було стверджувати, що в партії буде не менш як 75 примірників 1-го сорту?
ВАРІАНТ 2
Практична робота 1.
Дії над комплексними числами.
1. Знайти суму, різницю, добуток, частку двох комплексних чисел (5+4і) та (-2+3і).
2. В якій чверті розміщене комплексне число -3+і
3.
Розв’язати рівняння:
.
4.
Знайти координати точки М, що зображує
комплексне число
Практична робота 2
Дії над комплексними числами.
1.
Виконати дії в алгебраїчній формі.
Результат записати в тригонометричній
та показникових формах
.
Практична робота 3
Знаходження границь.
1. Функцію задано графіком, зображеним на рисунку:
Визначити при яких значеннях х функція від’ємна.
2.
Визначіть інтервали знакосталості
функції
.
3.Знайти
границю функції
.
4.
Знайти границю функції
.
5.
Знайти границю функції
.
Практична робота 4
Перша та друга визначні границі.
1.
Знайти границю функції
.
2. Знайти границю функції .
3. Знайти
точки розриву функції
.
Практична робота 5
Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.
1. Задана функція у = f(x). Знайти у.
1)
;
2)
;
3)
;
4)
;
5)
;
6) ;
7)
;
8)
;
2.
Знайти похідну другого порядку:
.
3. Написати рівняння дотичної та нормалі до кривої у = х3 у точці М(1;1).
Практична робота 6
Похідна. Схема повного дослідження і побудови графіка функції.
1.
Визначити екстремуми функції:
.
2. Знайти найбільше і найменше значення функції у заданому проміжку: .
3.
Знайти точки перегину та інтервали
опуклості і вгнутості графіку функції:
.
4. Знайти асимптоти таких ліній: .
5.
Провести повне дослідження функції і
накреслити її графік:
.
Практична робота 7
Невизначений інтеграл.
1. Розклавши підінтегральні функції за формулою , знайти такі інтеграли: а) ; б) .
2.
Безпосереднім інтегруванням знайти
інтеграл:
.
3.
Знайти інтеграл:
.
4.
Інтегруванням частинами знайти інтеграл:
5. Методом підстановки знайти інтеграл:
Практична робота 8
Визначений інтеграл.
1. Використовуючи метод підстановки, обчислити визначений інтеграл:
2.
Інтегруванням частинами обчислити
визначений інтеграл:
3. За
допомогою визначеного інтегралу
обчислити площу фігури, що обмежено
лініями:
Практична робота 9
Дії на векторами. Дії над матрицями.
1.
Визначити вершини і кути трикутника,
сторони якого задано рівняннями:
.
2. Знайти
визначники третього порядку:
3.
Розкладаючи за другим стовпчиком,
обчислити визначник:
.
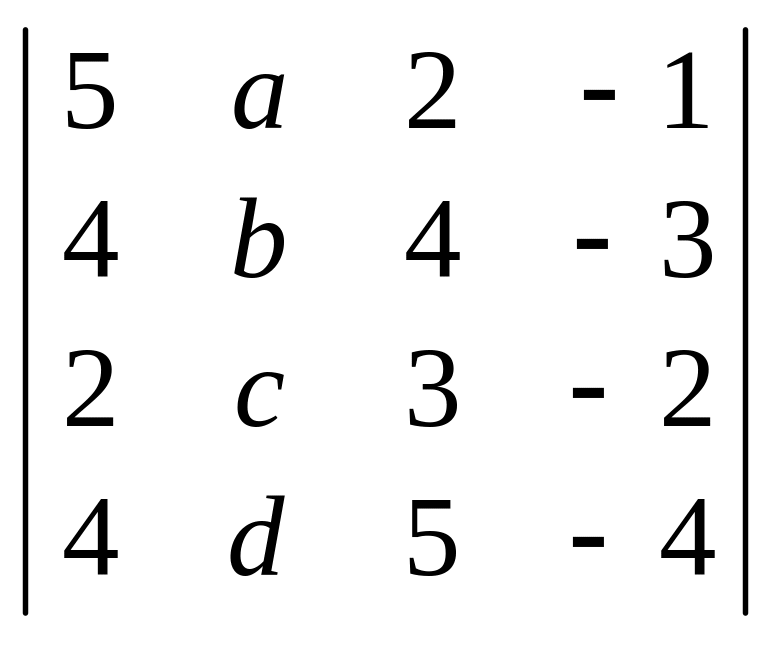4.
Знайти добутки матриць:
.
5.
Знайти обернені до таких матриць:
.
Практична робота 10
Дії над матрицями. Розв'язування систем лінійних рівнянь.
1.
Розв’язати систему лінійних рівнянь
за правилом Крамера. У разі залежності
коефіцієнтів системи рівнянь від
параметрів дослідити систему на
сумісність.
2.
Звести до матричного вигляду систему
рівнянь і розв’язати методом оберненої
матриці:
Практична робота 11
Система координат. Пряма та площина.
1.
На осі ординат знайти точки, що віддалені
від точки
на відстані 5 одиниць.
2.
Відрізок
між точками
і
поділено на п’ять рівних частин. Знайти
координати точок поділу.
3.
Скласти рівняння кола, що проходить
через три задані точки:
.
Практична робота 12
Загальне рівняння кривої другого порядку.
1. Звести
до канонічного вигляду рівняння кола
2.
Знаючи рівняння асимптот гіперболи
і одну з точок на гіперболі
,
скласти рівняння гіперболи.
3.
Визначити тип кривої другого порядку:
.
4.
Через точку
проведено площину перпендикулярно до
.
Написати її рівняння.
Практична робота 13
Дії з рядами.
1. Запишіть три перші члени ряду, а також
2. Запишіть
найпростішу формулу n-го
члена ряду та перевірте виконання
необхідної умови збіжності ряду:
3.
Перевірте виконання необхідної умову
збіжності ряду:
Практична робота 14
Дії з рядами.
1. Дослідити збіжність ряду, користуючись безпосередньо означенням збіжності ряду. Знайти суму ряду:
2.
За допомогою ознак порівняння дослідити
збіжність ряду:
3.
Дослідити збіжність ряду за допомогою
ознаки Даламбера:
Практична робота 15
Розв'язування диференційних рівнянь першого порядку
1.
Розв’язати диференційне рівняння
першого порядку:
2. Знайти частинні розв’язки диференціального рівнянь, що задовольняють задані початкові умови: при . (Задача Коші.)
3.
Знайти
частинні розв’язки диференціального
рівнянь:
,
при
.
Практична робота 16
Розв'язування однорідних диференційних рівнянь
1.
Знайти загальний розв’язок однорідного
диференціального рівняння:
2.
Розв’язати диференціальне рівняння в
повних диференціалах:
3. Розв’язати диференціальне рівняння першого порядку:
4. Розв’язати
рівняння
при
Практична робота 17
Дії над ймовірностями.
1. Партія складається зі стандартних і нестандартних деталей, які ретельно перемішані. З неї навмання беруть дві деталі. Визначити:
простір елементарних подій;
множини елементарних подій для таких подій:
а) — поява однієї стандартної і однієї нестандартної деталей;
б) — поява не менш як однієї стандартної деталі;
в) — поява не більш як однієї стандартної деталі.
2. Партія складається з 20 виробів, з яких 8 виробів 1-го сорту, 6—2-го, 2—3-го сорту, а решта — браковані. Навмання беруть 4 вироби. Знайти ймовірність того, що серед них виявилося 2 вироби 1-го сорту, 1—2-го сорту і 1 бракований.
3. У шухляді є вісім однотипних деталей, три з яких браковані (решта — стандартні). Навмання з шухляди беруть три деталі. Знайти імовірність подій Аі де і — число бракованих деталей серед взятих (і = 0, 1, 2, 3).
4. Серед 18 телевізорів, що продаються, 6 вимагають додаткового регулювання. Знайти ймовірність того, що з п’яти куплених телевізорів два потребуватимуть додаткового регулювання.
5. Від аеровокзалу відправились два автобуси. Імовірність своєчасного прибуття кожного з них дорівнює 0,92. Знайти ймовірність такої події:
А — обидва автобуси прибудуть своєчасно;
В — обидва автобуси запізняться;
С — тільки один автобус прибуде своєчасно.
6. Для посіву пшениці заготовлено насіння, серед якого 95 % 1-го сорту, 3 % 2-го та 2 % 3-го сорту. Імовірність того, що з насінини виросте колосок, в якому не менш ніж 50 зерен, для 1-го сорту насіння становить 0,5, для 2-го сорту — 0,2, для 3-го — 0,1. Знайти ймовірність того, що навмання взятий колосок у разі такого посіву матиме не менш як 50 зерен.
7. Для забезпечення роботи на деякому будівельному об’єкті автопідприємство має 6 автомобілів. Імовірність виходу кожного автомобіля на лінію в першу зміну дорівнює 0,8. Знайти ймовірність нормальної роботи автопідприємства, якщо для цього в першу зміну потрібно мати на лінії не менш як 4 автомобілі.
8. На трьох верстатах-автоматах виготовляються однакові деталі. Перший верстат дає 5 % браку, другий — 7 %, третій — 9 %. Із продукції кожного верстата навмання взято по одній деталі. Знайти ймовірність того, що серед них виявилось:
0, 1, 2, 3 придатних;
принаймні одна деталь придатна;
принаймні одна деталь бракована.
ВАРІАНТ 3
Практична робота 1.
Дії над комплексними числами.
1. Виконати дії і(1+і)
2. Обчислити: і16
3. Розв’язати рівняння: .
4.
Знайти число спряжене з числом
Практична робота 2
Дії над комплексними числами.
1.
Виконати дії в алгебраїчній формі.
Результат записати в тригонометричній
та показникових формах
.
Практична робота 3
Знаходження границь.
1. Функцію задано графіком, зображеним на рисунку:
Визначити при яких значеннях х функція спадає.
2.
Знайти область визначення функції
.
3.Знайти границю функції .
4.
Знайти границю функції
.
5.
Знайти границю функції
.
Практична робота 4
Перша та друга визначні границі.
1.
Знайти границю функції
.
2. Знайти границю функції .
3. Який
характер має розрив функції
в точці х=1?
Практична робота 5
Похідна, диференціал суми, добутку, частки, складеної та оберненої функції.
1. Задана функція у = f(x). Знайти у.
1)
;
2)
;
3)
;
4)
;
5)
;
6) ;
7) ;
8)
;
2.
Знайти похідну другого порядку:
.
3. Нехай — рівняння вільного руху тіла, g — прискорення його вільного падіння. Знайти миттєву швидкість тіла в будь-який момент часу; у момент часу t = 2 c.
Практична робота 6
Похідна. Схема повного дослідження і побудови графіка функції.
1.
Визначити екстремуми функції:
.
2. Знайти найбільше і найменше значення функції у заданому проміжку: .
3. Знайти точки перегину та інтервали опуклості і вгнутості графіку функції: .
4. Знайти асимптоти таких ліній: .
5.
Провести повне дослідження функції і
накреслити її графік:
.
Практична робота 7
Невизначений інтеграл.
1. Розклавши підінтегральні функції за формулою , знайти такі інтеграли: а) ; б) .
2.
Безпосереднім інтегруванням знайти
інтеграл:
.
3.
Знайти інтеграл:
.
4.
Інтегруванням частинами знайти інтеграл:
5. Методом підстановки знайти інтеграл:
Практична робота 8
Визначений інтеграл.
1.
Використовуючи метод підстановки,
обчислити визначений інтеграл:
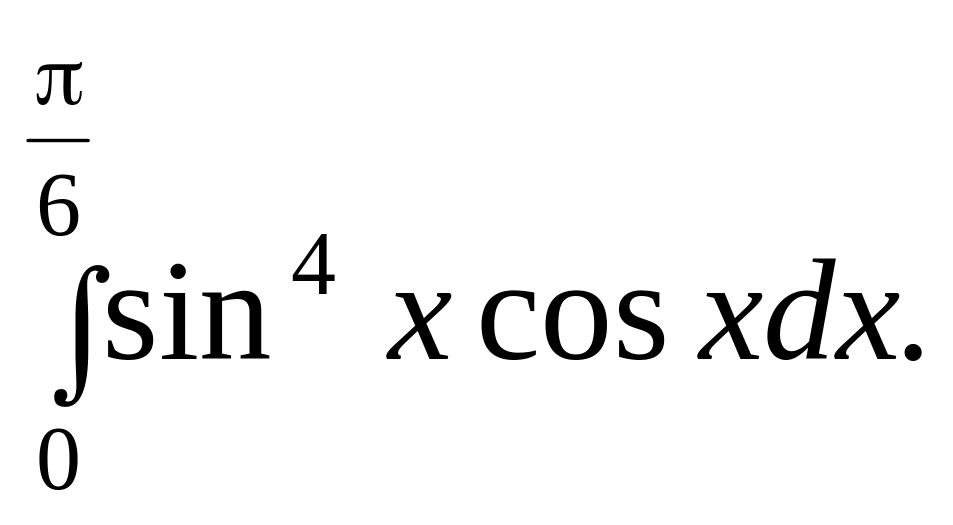
2. Інтегруванням частинами обчислити визначений інтеграл:
3. За
допомогою визначеного інтегралу
обчислити площу фігури, що обмежено
лініями:
Практична робота 9
Дії на векторами. Дії над матрицями.
1.
У трикутнику з вершинами
проведені висота
і медіана
Написати рівняння сторони АС,
медіани ВМ
і висоти
.
2. Знайти
визначники третього порядку: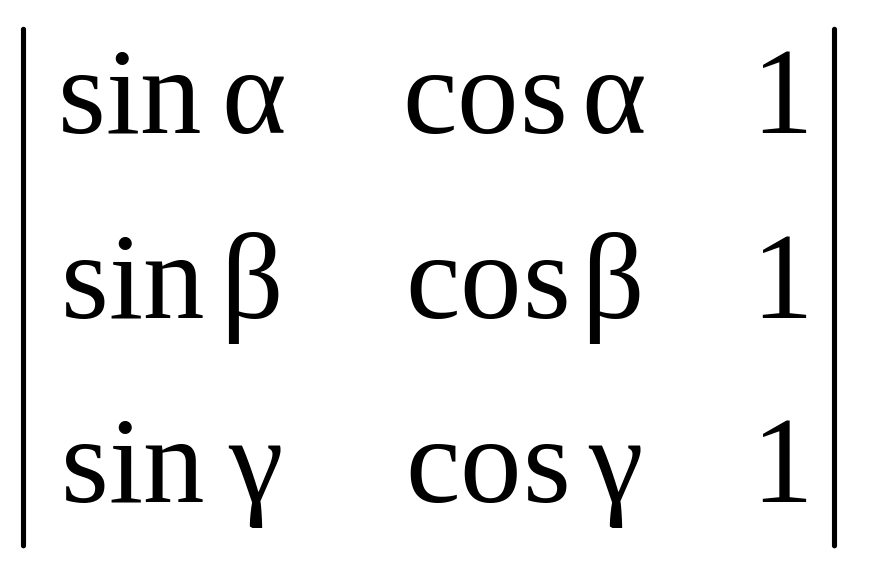
3.
Обчислити визначник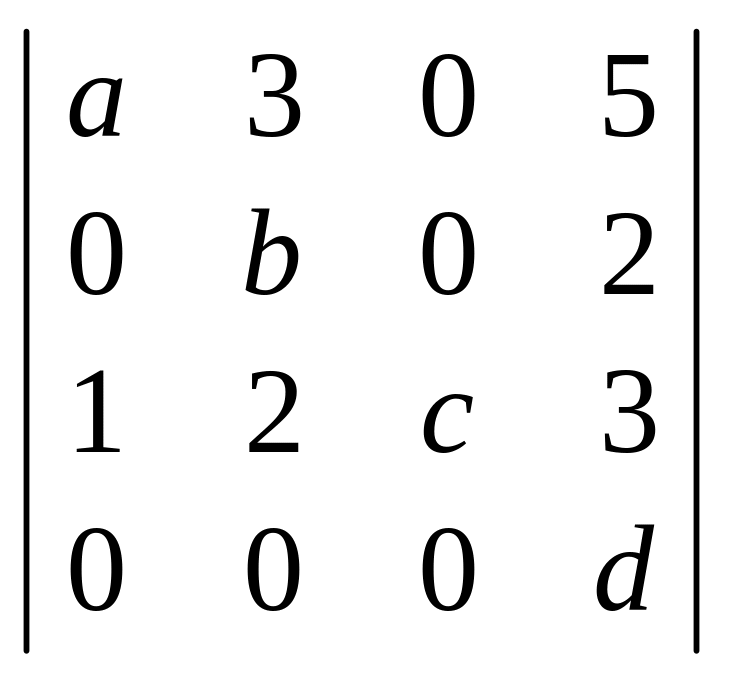
.
4.
Знайти добутки матриць: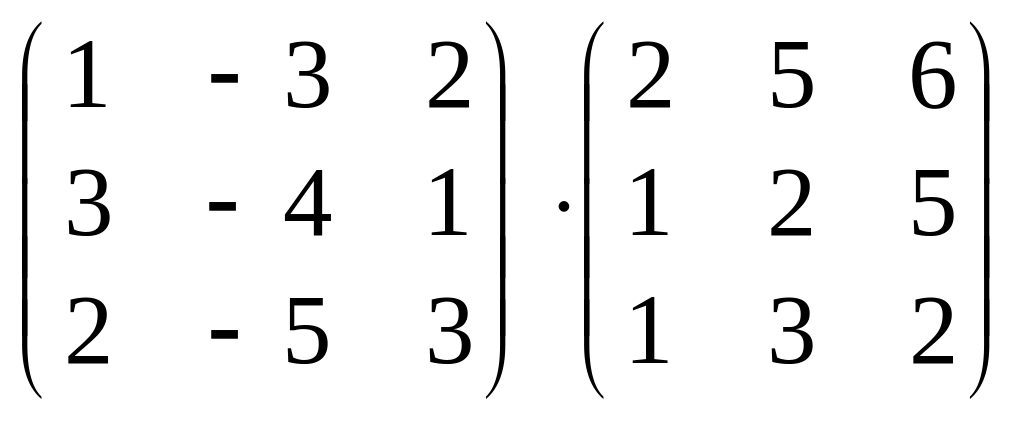
.
5.
Знайти обернені до таких матриць:
.
Практична робота 10
Дії над матрицями. Розв'язування систем лінійних рівнянь.
1.
Розв’язати систему лінійних рівнянь
за правилом Крамера. У разі залежності
коефіцієнтів системи рівнянь від
параметрів дослідити систему на
сумісність.
2. Звести до матричного вигляду систему рівнянь і розв’язати методом оберненої матриці:
Практична робота 11
Система координат. Пряма та площина.
1.
Обчислити периметр і площу трикутника
за координатами його вершин:
і
2. У трикутнику з вершинами проведені висота і медіана Написати рівняння сторони АС, медіани ВМ і висоти .
3. Знайти відстані точок від прямої .
Практична робота 12
Загальне рівняння кривої другого порядку.
1. Звести до канонічного вигляду рівняння кола .
2. Дано рівняння еліпса: . Обчислити довжини осей, координати фокусів та його ексцентриситет.
3.
Визначити тип кривої другого порядку:
.
4. Написати
рівняння площини, що проходить через
точку
і перпендикулярна до площин
і
.
Практична робота 13
Дії з рядами.
1. Запишіть три перші члени ряду, а також
2. Запишіть
найпростішу формулу n-го
члена ряду та перевірте виконання
необхідної умови збіжності ряду:
3. Перевірте виконання необхідної умову збіжності ряду:
Практична робота 14
Дії з рядами.
1. Дослідити збіжність ряду, користуючись безпосередньо означенням збіжності ряду. Знайти суму ряду:
2.
За допомогою ознак порівняння дослідити
збіжність ряду:
3. Дослідити збіжність ряду за допомогою ознаки Даламбера:
Практична робота 15
Розв'язування диференційних рівнянь першого порядку
1.
Розв’язати диференційне рівняння
першого порядку:
2. Знайти частинні розв’язки диференціального рівнянь, що задовольняють задані початкові умови: при . (Задача Коші.)
3.
Знайти
частинні розв’язки диференціального
рівнянь:
,
при
.
Практична робота 16
Розв'язування однорідних диференційних рівнянь
1.
Знайти загальний розв’язок однорідного
диференціального рівняння:
2.
Розв’язати диференціальне рівняння в
повних диференціалах:
3. Розв’язати диференціальне рівняння першого порядку: