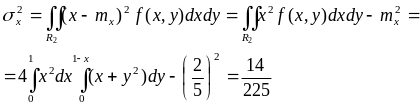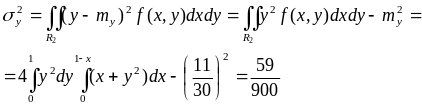1.8 Системы случайных величин

Систему двух случайных величин (X,Y) можно изобразить случайно точкой на плоскости.

Событие, состоящее в попадании случайной точки (X;Y) в область D, принято обозначать в виде (X;Y) D.

Закон распределения системы непрерывных случайных величин (X,Y) будем задавать с помощью функции плотности вероятности f(x,y).

Вероятность попадания случайной точки (X,Y) в область D определяется ра­венством

Функция плотности вероятности обладает следующими свойствами:

Если все случайные точки (X;Y) принадлежат конечной области D , то послед­нее условие принимает вид

. (1.8.1)

Математическое ожидание дискретных случайных величин X и Y, входящих в систему, определяются по формулам

, (1.8.2)

а математические ожидания непрерывных случайных величии - по формулам

(1.8.3)

(1.8.4)

Точка ( ; ) называется центром рассеивания системы случайных величин (X,Y).

Математические ожидания и т_у можно найти и проще, если случайные величины X и Y независимы. В этом случае из законов распределения этих случайных величин можно определить математические ожидания и т_у по формуле

(1.8.5)

(1.8.6)

Дисперсии дискретных случайных величин X и Y определяются по формулам

; (1.8.7)

. (1.8.8)

Дисперсии же непрерывных случайных величин X и Y, входящих в систему, находятся по формулам

; (1.8.9)

. (1.8.10)

Средние квадратичные отклонения случайных величин X и Y определяются по формулам

(1.8.11)

Для вычисления дисперсий могут быть применены формулы

(1.8.12)

Важную роль в теории систем случайных величин играет так называемый корреляционный момент (ковариация)

(1.8.13)

Для дискретных случайных величин корреляционный момент находится по формуле

(1.8.14)

а для непрерывных – по формуле

(1.8.15)

Корреляционный момент можно также найти по формуле

(1.8.16)

Здесь

для дискретных величин X и Y и

(1.8.17)

для непрерывных величин.

Случайные величины X и Y называются независимыми, если вероятность одной из них принимает значение, лежащее в любом промежутке области ее значений, и не зависит от того, какое значение приняла другая величина. В этом случае

M(XY)=M(X)M(Y);

Для характеристики связи между величинами X и Y рассматривается так называемый коэффициент корреляции

(1.8.18)

являющийся безразмерной величиной.

Если случайные величины X и Y независимы, то =0. Если же случайные величины X и Y связаны точной линейной зависимостью Y=aX+b, то = sgna ,т.е. =1 при а > 0 и = -1 при а < 0. Вообще же коэффициент корреляции удовлетворяет условию

-1 1.

Задача 1.8.1

Дана таблица 1.8.1, определяющая закон распределения системы двух случайных величин (X,Y):

Таблица 1.8.1

X y	20	40	60
10	3		0
20	2	4	2
30		2	5

Найти: 1) коэффициент ; 2) математическое ожидание и ;

3) дисперсии и ; 4) коэффициент корреляции .

Решение.

Таблица 1.8.2 Таблица 1.8.3

X Y	20	40	60	∑
10	3		0	4
20	2	4	2	8
30		2	5	8
∑	6	7	7	∑20 =1

X y	20	40	60
10	3		0	4
20	2	4	2	8
30		2	5	8
	6	7	7	20 =1

	-21	-1	19
-12	3		0
-2	2	4	2
8		2	5

Найдём из условий (1.8.1):

Вычислим дисперсии по формулам:

или ,

или ,

Вычислим и и составим таблицу 1.8.3

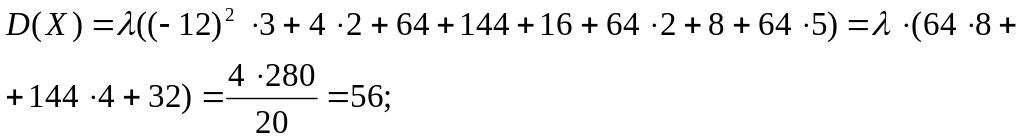
Определим ковариацию по формуле

Вычислим коэффициент корреляции:

Задача 1.8.2

Пусть область возможных значений случайной величины – треугольник с границами x=0, y=0 и x+y=1. Плотность распределения , где А – нормированный множитель. Найдём Область D возможных значений приведена на рисунке 1.8.1.

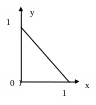Рис. 1.8.1

Из условия нормировки находим

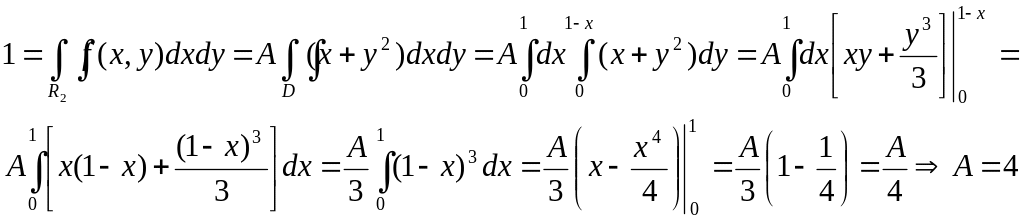
Плотность распределения величин x при

Таким образом,

п ри x<0

при

при x>1

Аналогично при имеем

_.

Таким образом,

_.

_.
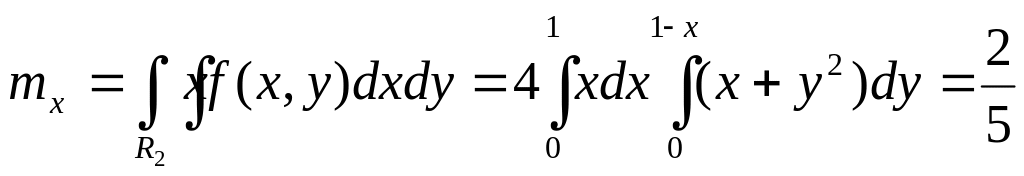
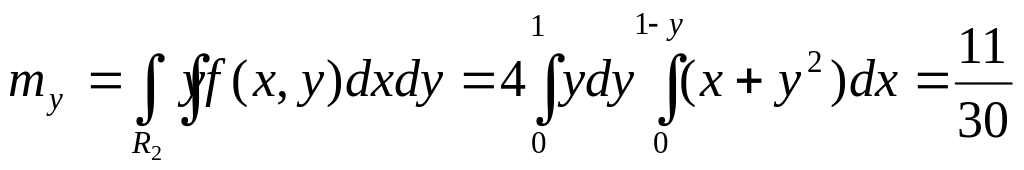