Тема 3. Теория массового обслуживания

1. Задачи теории массового обслуживания. Классификация систем массового обслуживания (СМО)

Функционирование многих реальных сложных систем носит характер обслуживания поступающих в систему заявок. Для выполнения совокупности действий или операций, имеются специальные каналы.

Любая СМО предназначена для обслуживания какого-то потока заявок (или требований), поступающих в какие-то случайные моменты времени. Обслуживание заявки продолжается какое-то случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания приводит к тому, что в какие-то периоды времени на входе СМО скапливается излишне большое число заявок, в другие же периоды СМО будет работать с недогрузкой или вообще простаивать.

Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем, состояние СМО меняется скачком в моменты появления каких-то событий (или прихода новой заявки, или окончания обслуживания или момента, когда заявка, которой надоело ждать, покидает очередь).

Предмет теории МО – построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками – показателями эффективности СМО, описывающими и способность справляться с потоком заявок. В качестве таких показателей могут быть использованы различные величины, например: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди; среднее время ожидания обслуживания; вероятность того, что число заявок в очереди превысит какое-то значение и т.д.

Математический анализ работы СМО очень облегчается, если процесс этой работы – Марковский.

СМО можно делить на классы по ряду признаков.

Первое деление на СМО с отказами и с очередью. В СМО с отказами заявка, поступившая в момент, когда все каналы заняты, получает отказ, покидает СМО и в дальнейшем процессе обслуживания не участвует. Примеры СМО с отказами встречаются в телефонии: заявка на разговор, пришедшая в момент, когда все каналы связи заняты, получает отказ и покидает СМО необслуженной. В СМО с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможности быть обслуженной.

СМО очередью подразделяется на разные виды, в зависимости от того, как организована очередь – ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания (так называемые «СМО с нетерпеливыми заявками»).

СМО можно так же классифицировать по дисциплине обслуживания. Заявки могут обслуживаться либо в порядке поступления (раньше пришла, раньше обслуживается), либо в случайном порядке. Нередко встречаются так называемое обслуживание с приоритетом – некоторые заявки обслуживаются вне очереди. Приоритет может быть как абсолютный – когда заявка с более высоким приоритетом «вытесняет» из обслуживания заявку с низшим приоритетом, так и относительным – когда начатое обслуживание доводиться до конца, а заявка с более высоким приоритетом имеет лишь право на лучшее место в очереди.

Существуют СМО с так называемым многофазовым обслуживанием, состоящим из нескольких последовательных этапов (например, покупатель, пришедший в магазин, должен сначала выбрать товар, затем оплатить его в кассе, затем получить на контроле).

Кроме этих признаков, СМО делятся на 2 класса: открытые и замкнутые. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО – зависят. Например, если один рабочий обслуживает группу станков, время от времени требующих наладки, то интенсивность потока «требований» со стороны станков зависит от того, сколько их уже неисправно и ждет наладки.

Наиболее употребляемой является классификация Кендалла. В соответствии с этой классификацией тип СМО задается четверкой символов, 2 первых из которых – буквы, а третий и четвертый – цифры. Первая буква определяет входящий поток требований. При этом случайные продолжительности интервалов между моментами поступления требований независимы, одинаково распределены и имеют

M – показательное

D – вырожденное

E – эрланговое

G – произвольное распределение.

Те же буквы на втором месте аналогичным образом задают распределение времени обслуживания. Цифра, стоящая на третьей позиции, определяет число обслуживающих каналов, а четвертая – количество мест для ожидания.

2. СМО M/M/n/0

Рассмотрим элементарный случай, когда входящий поток – простейший, продолжительность обслуживания экспоненциальная, места для ожидания в очереди отсутствуют. Анализ может быть проведен с использованием теории Марковских процессов.

Введем множество возможных состояний системы:

все каналы системы свободны;

один канал занят, остальные свободны;

^{……………………………………………………………………………}

все n каналов системы заняты.

Будем считать, что интенсивность входящего потока заявок равна , а закон распределения продолжительности обслуживания имеет вид , где интенсивность обслуживания выражает количественно среднее число заявок, которое каждый канал системы в состоянии обслужить

, среднее время обслуживания.

Нарисуем граф переходов системы

Система дифференциальных уравнений для вероятностей состояний имеет вид:

Систему уравнений необходимо дополнить условием нормировки . Для решения системы используют преобразование Лапласа. При этом получим следующую систему линейных алгебраических уравнений:

Решив эту систему уравнений и выполнив обратное преобразование Лапласа, получим соотношение для . Для оценки эффективности СМО интерес представляет асимптотическое поведение систему при . В этом случае процесс в системе приобретает установившийся характер и поэтому . Тогда уравнения системы упрощаются к виду:

Введем переменную . Тогда

Откуда легко видеть, что Поэтому

.

Тогда

Таким образом, вероятности всех состояний выражены через . Для расчета используем условие нормировки.

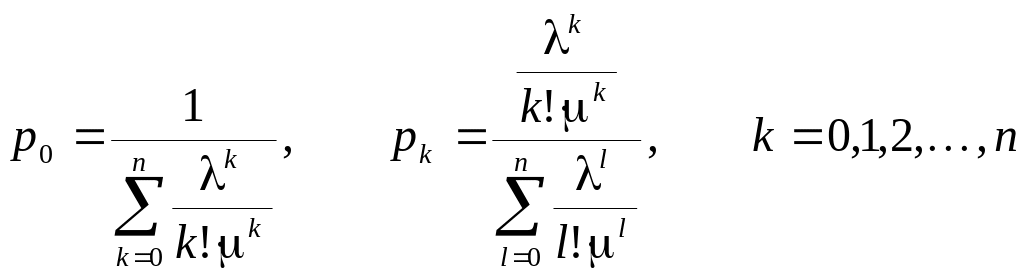
Введем параметр , который называется приведенной интенсивностью входного потока. Тогда

Эти соотношения называются формулами Эрланга. С использованием этих формул легко рассчитать вероятность отказа системы

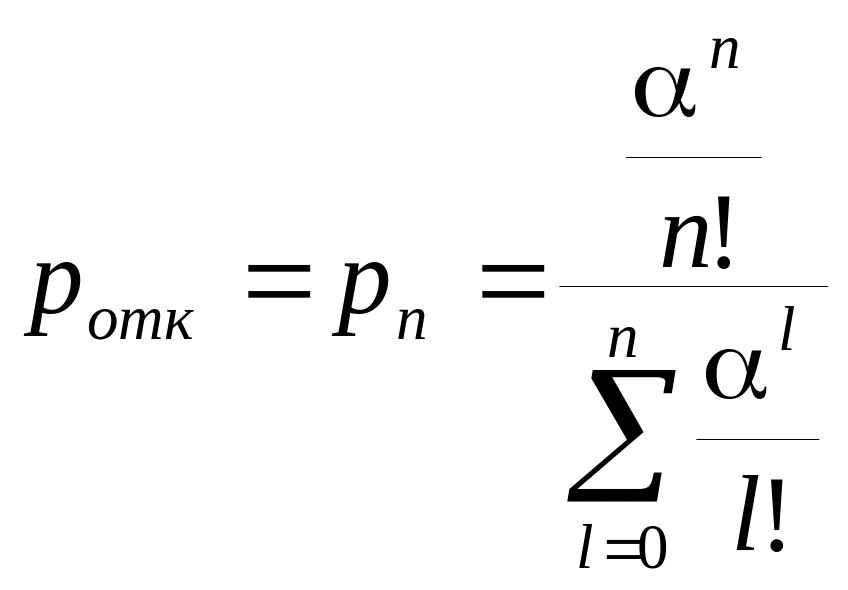
Можно найти относительную пропускную способность – вероятность того, что заявка будет обслужена

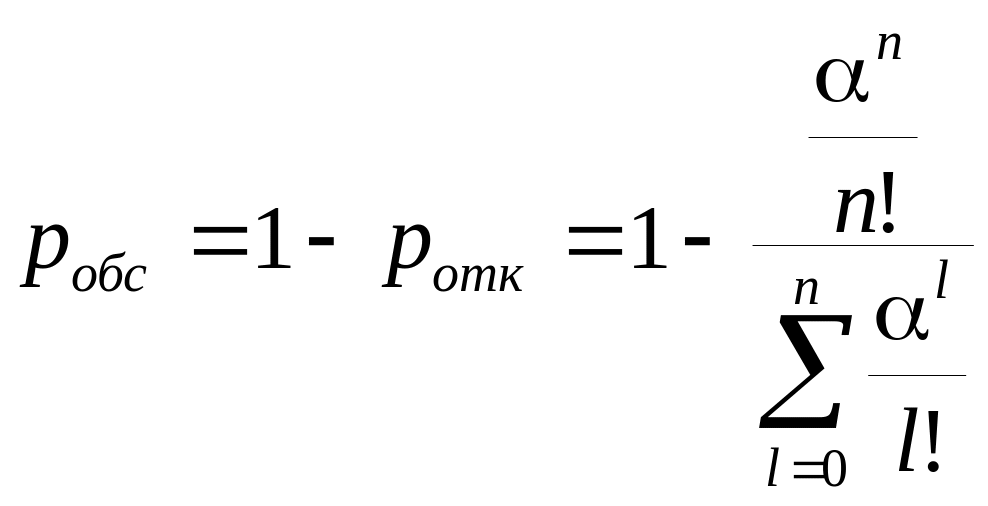
Абсолютную пропускную способность получим, умножая интенсивность потока заявок на : .

Среднее число занятых каналов можно найти, как математическое ожидание дискретной случайной величины с возможными значениями 0,1,…,n и вероятностями этих значений

Введем . Тогда

С другой стороны, среднее число занятых каналов можно найти по другому. Абсолютная пропускная способность - это интенсивность потока обслуженных системой заявок. Каждый занятый канал в единицу времени обслуживает в среднем заявок. Значит среднее число занятых каналов равно:

.