
- •Линейное подпространство l в r3 порождено векторами , , . Принадлежит ли вектор этому подпространству?
- •2. Найдите систему линейных уравнений, задающих линейное подпространство, натянутое на следующую систему векторов .
- •4. Линейное отображение a имеет в базисе матрицу . Найдите матрицу этого отображения в базисе
- •5. Запишите матрицу линейного оператора, который переводит векторы соответственно в и . Какой вектор получится, если применить этот оператор .
- •6. Найдите базисы ядра и образа (указав размерность этих линейных подпространств) линейного отображения, заданного матрицей .
- •7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .
- •10. Найдите действительные собственные числа и собственные векторы матрицы .
- •12. Найдите собственные числа и собственные векторы матрицы . Объяснить, почему ее нельзя привести к диагональному виду.
- •13. Постройте базис в r3, в котором матрица следующего линейного оператора принимает диагональный вид .
- •17. В r4 дано линейное подпространство l, являющееся линейной оболочкой векторов .
- •Найти базис ортогонального дополнения ;
- •Разложить вектор на сумму ортогональной проекции на l и ортогональную составляющую.
- •18. Найти ортонормированный базис из собственных векторов оператора, заданного в ортонормированном базисе симметричной матрицей .
- •19. Может ли данная билинейная форма
- •20. Могут ли формулы и быть формулами одной и той же квадратичной формы в разных базисах?
- •22. Найдите ортонормированный базис, в котором квадратичная форма имеет канонический вид.
- •23. Привести квадратичную форму .
- •24. При каких квадратичная форма является положительно или отрицательно определенной?
- •25. Найти все значения параметра , при которых квадратичная форма положительно определена.
10. Найдите действительные собственные числа и собственные векторы матрицы .
Решение. 1) Решаем
характеристическое уравнение
![]() или
или
 или
или
![]() .
.
Следовательно,
![]() - собственные числа.
- собственные числа.
2) Находим собственные
вектора, решая систему
![]() .
.
![]() .
Решаем систему
.
Решаем систему
![]() .
.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() соответствующий
(другие собственные вектора имеют вид
соответствующий
(другие собственные вектора имеют вид
![]() ,
где С – произвольные действительные
числа).
,
где С – произвольные действительные
числа).
![]() .
Решаем систему
.
Решаем систему
![]() .
.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() соответствующий
(другие собственные вектора имеют вид
соответствующий
(другие собственные вектора имеют вид
![]() ,
где С – произвольные действительные
числа).
,
где С – произвольные действительные
числа).
![]() .
Решаем систему
.
Решаем систему
![]() .
.
Полагая
,
получаем собственный вектор
![]() соответствующий
соответствующий
![]() (другие собственные вектора имеют вид
(другие собственные вектора имеют вид
![]() ,
где С – произвольные действительные
числа).
,
где С – произвольные действительные
числа).
11.
Вычислите
матрицу (арифметические выражения можно
не упрощать):
 .
.
Решение.

12. Найдите собственные числа и собственные векторы матрицы . Объяснить, почему ее нельзя привести к диагональному виду.
Решение. 1) Решаем характеристическое уравнение или
![]() или
или
![]() или
или
![]() .
.
Следовательно,
![]() - собственные число кратности 2.
- собственные число кратности 2.
2) Находим собственные вектора, решая систему .
![]() .
Решаем систему
.
Решаем систему
![]() .
.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() соответствующий
.
соответствующий
.
Данную матрицу нельзя привести к диагональному виду, т.к. не существует базиса из собственных линейно независимых векторов (у нас 1 вектор, а надо 2 линейно независимых вектора, чтобы они давали базис в R2).
13. Постройте базис в r3, в котором матрица следующего линейного оператора принимает диагональный вид .
Решение. 1) Решаем характеристическое уравнение или
 или
или
![]() .
.
Следовательно,
- собственное число кратности 2,
![]() собственное число кратности 1.
собственное число кратности 1.
2) Находим собственные вектора, решая систему .
. Решаем систему
![]() .
.
Здесь
- базисная переменная, а
![]() - небазисные переменные.
- небазисные переменные.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() .
.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() .
.
. Решаем систему
 .
.
Здесь
![]() - базисные переменные, а
- небазисная переменная.
- базисные переменные, а
- небазисная переменная.
Полагая
,
получаем собственный вектор
![]() .
.
3) Следовательно, в базисе , , , состоящем из собственных векторов, матрица А имеет диагональный вид (на диагонали стоят собственные числа):
 .
.
14. Пусть
V=R4
- евклидово пространство со стандартным
скалярным произведением. Линейное
подпространство U
- линейная
оболочка векторов
 .
С помощью процесса ортогонализации
найдите ортогональный базис U.
.
С помощью процесса ортогонализации
найдите ортогональный базис U.
Решение. 1) Проверим,
что вектора линейно независимые, для
чего находим ранг матрицы А, столбцами
которой являются вектора
![]() ,
,![]() ,
,![]() .
.
 ,
то rang(A)=3,
,
то rang(A)=3,
что означает, что вектора , , линейно независимые.
2) Применим процесс
ортогонализации (Грама – Шмидта):
 ,
,
![]() - скалярные
произведения.
- скалярные
произведения.
Производим
вычисления:
![]() ,
,
 ;
;

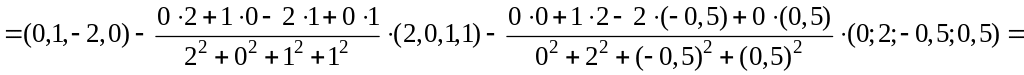
 .
.
Итак:
![]() ,
,
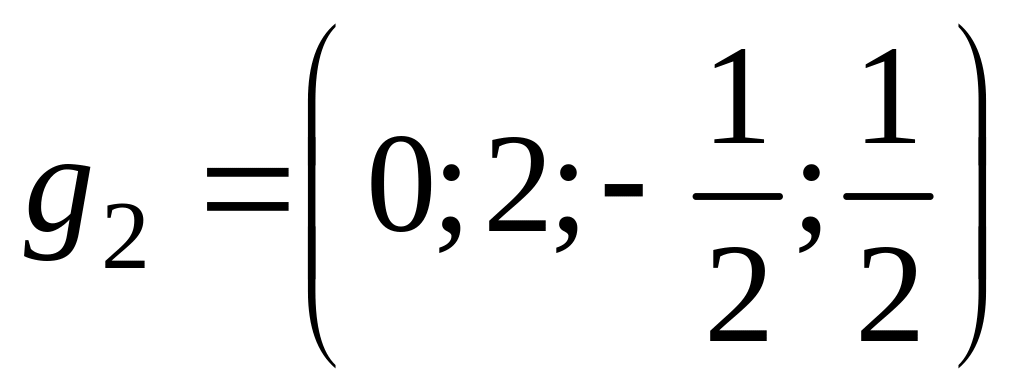 ,
,
 - ортогональный
базис.
- ортогональный
базис.
Проверка:
![]() ,
,
![]() ,
,
![]() .
.
15. Пусть
V=R4
- евклидово пространство со стандартным
скалярным произведением. U
– подпространство
V,
задаваемое системой уравнений
 .
Найдите ортогональную проекцию на
подпространство U
и
ортогональную составляющую вектора
(4;2;3;5).
.
Найдите ортогональную проекцию на
подпространство U
и
ортогональную составляющую вектора
(4;2;3;5).
Решение. 1) Находим базис U – фундаментальные решения системы. Применим метод Гаусса:
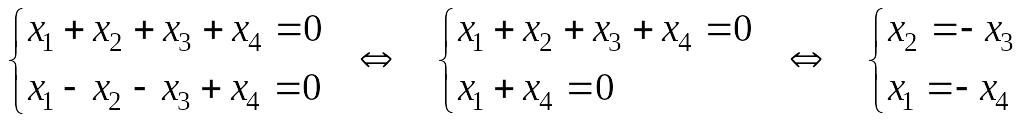 .
.
Следовательно,
- базисные переменные,
![]() - небазисные переменные.
- небазисные переменные.
При
![]() ,
из системы получаем 1-е фундаментальное
решение:
,
из системы получаем 1-е фундаментальное
решение:
![]() .
.
При
![]() ,
из системы получаем 2-е фундаментальное
решение:
,
из системы получаем 2-е фундаментальное
решение:
![]() .
.
Базис U: , .
2) Построим ортогональный базис U. Применяем процесс ортогонализации Грама – Шмидта.
![]() ,
,
 .
.
Т.о. базис
,
![]() - ортогональный базис U.
- ортогональный базис U.
3) (подробно). Пусть
![]() ортогональная
проекция
ортогональная
проекция
![]() на U,
на U,
![]() ортогональная
составляющая.
Причем из
определения этих векторов следует, что
ортогональная
составляющая.
Причем из
определения этих векторов следует, что
![]() (см. рисунок). Т.к.
(см. рисунок). Т.к.
![]() ,
то существуют
,
то существуют
![]() ,
что
,
что
![]() ,
т.е.
выражается через базис.
,
т.е.
выражается через базис.
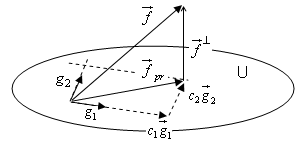
Т.к.
![]() ,
то
,
то
![]() ортогонален любому вектору из
ортогонален любому вектору из
![]() ,
в частности базисным векторам. Тогда,
т.к.
,
в частности базисным векторам. Тогда,
т.к.
![]() ,
то из того, что скалярные произведения
равны нулю, получаем:
,
то из того, что скалярные произведения
равны нулю, получаем:
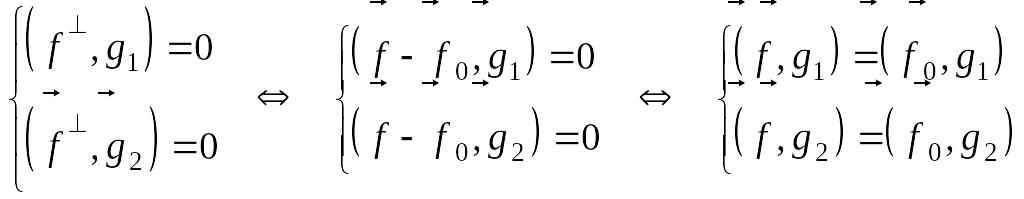
Производим
вычисления и находим
![]() :
,
:
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
т.к.
,
т.к.
![]() - ортогональные,
- ортогональные,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теперь система принимает вид:
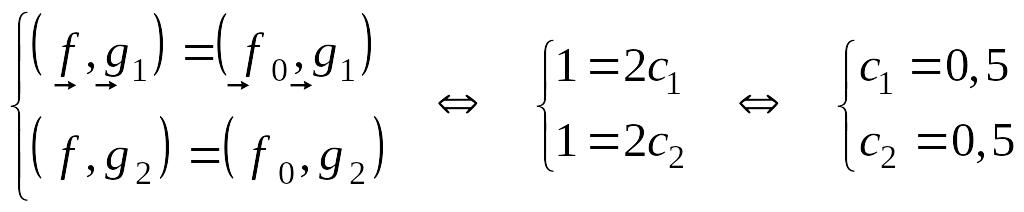 .
.
Ортогональная
проекция:
![]() .
.
Ортогональная
составляющая:
![]() .
.
16. Пусть
V=R3
- евклидово пространство со стандартным
скалярным произведением. Самосопряженный
оператор A
задан в
стандартном ортонормированном базисе
матрицей
 .
Найдите канонический вид оператора и
ортонормированный базис пространства
V,
состоящий
из собственных векторов A.
.
Найдите канонический вид оператора и
ортонормированный базис пространства
V,
состоящий
из собственных векторов A.
Решение.
Самосопряженность оператора А означает,
что для любых векторов
![]() справедливо равенство
справедливо равенство
![]() ,
где
,
где
![]() - скалярное произведение.
- скалярное произведение.
Теорема 1. Для того, чтобы преобразование А было самосопряженным необходимо и достаточно, чтобы в ортогональном нормированном базисе (в частности в стандартном) его матрица была симметричной.
Известно, что для самосопряженного оператора собственные значения вещественны, а собственные вектора, соответствующие различным собственным значениям - ортогональные. В ортонормированном собственном базисе матрица преобразования А имеет диагональный вид (где по диагонали стоят вещественные собственные значения).
1) Решаем характеристическое уравнение или
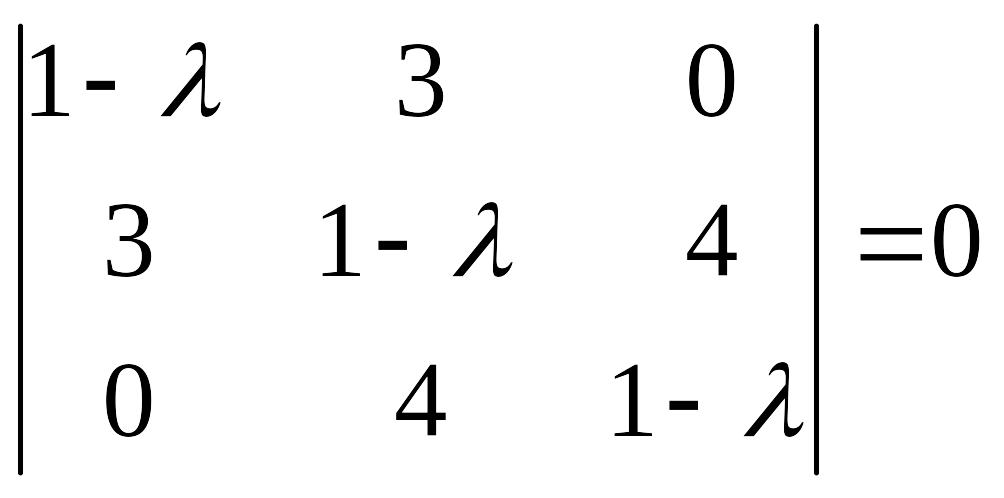 или
или
![]() .
.
Следовательно,
![]() - собственное значения.
- собственное значения.
2) Находим собственные вектора, решая систему .
![]() .
Решаем систему
.
Решаем систему
 .
.
Здесь
![]() - базисные переменные, а
- базисные переменные, а
![]() - небазисная переменная.
- небазисная переменная.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() .
.
![]() .
Решаем систему
.
Решаем систему
 .
.
Здесь - базисные переменные, а - небазисная переменная.
Полагая
![]() ,
получаем собственный вектор
,
получаем собственный вектор
![]() .
.
![]() .
Решаем систему
.
Решаем систему
 .
.
Здесь - базисные переменные, а - небазисная переменная.
Полагая
,
получаем собственный вектор
![]() .
.
Вектора
,
![]() ,
- ортогональный собственный базис.
,
- ортогональный собственный базис.
3) Построим ортонормированный базис:
 ,
,
![]() ,
,
 .
.
4) Канонический вид оператора А в ортонормированном собственном базисе:
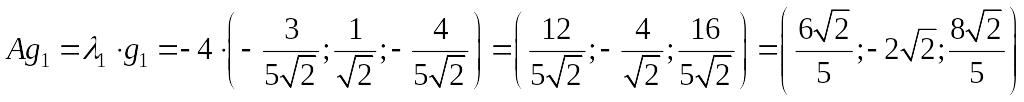 ,
,
![]() ,
,
 .
.
Матрица оператора
А в базисе
![]() имеет вид:
имеет вид:
 .
.
