
- •Линейное подпространство l в r3 порождено векторами , , . Принадлежит ли вектор этому подпространству?
- •2. Найдите систему линейных уравнений, задающих линейное подпространство, натянутое на следующую систему векторов .
- •4. Линейное отображение a имеет в базисе матрицу . Найдите матрицу этого отображения в базисе
- •5. Запишите матрицу линейного оператора, который переводит векторы соответственно в и . Какой вектор получится, если применить этот оператор .
- •6. Найдите базисы ядра и образа (указав размерность этих линейных подпространств) линейного отображения, заданного матрицей .
- •7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .
- •10. Найдите действительные собственные числа и собственные векторы матрицы .
- •12. Найдите собственные числа и собственные векторы матрицы . Объяснить, почему ее нельзя привести к диагональному виду.
- •13. Постройте базис в r3, в котором матрица следующего линейного оператора принимает диагональный вид .
- •17. В r4 дано линейное подпространство l, являющееся линейной оболочкой векторов .
- •Найти базис ортогонального дополнения ;
- •Разложить вектор на сумму ортогональной проекции на l и ортогональную составляющую.
- •18. Найти ортонормированный базис из собственных векторов оператора, заданного в ортонормированном базисе симметричной матрицей .
- •19. Может ли данная билинейная форма
- •20. Могут ли формулы и быть формулами одной и той же квадратичной формы в разных базисах?
- •22. Найдите ортонормированный базис, в котором квадратичная форма имеет канонический вид.
- •23. Привести квадратичную форму .
- •24. При каких квадратичная форма является положительно или отрицательно определенной?
- •25. Найти все значения параметра , при которых квадратичная форма положительно определена.
6. Найдите базисы ядра и образа (указав размерность этих линейных подпространств) линейного отображения, заданного матрицей .
Решение. Очевидно,
что данное линейное преобразование
действует
![]() ,
т.к. умножение матриц
,
т.к. умножение матриц
![]() определено, когда количество столбцов
1-й матрицы равно количеству строк
второго вектора (в нашем случае 4), а
полученная матрица имеет размерность
определено, когда количество столбцов
1-й матрицы равно количеству строк
второго вектора (в нашем случае 4), а
полученная матрица имеет размерность
![]() (т.к. в матрице A
5 строк).
(т.к. в матрице A
5 строк).
Совокупность N векторов x таких, что Ax=0, называется ядром преобразования A.
Совокупность M
векторов вида Ax,
когда x
пробегает все R
(в нашем случае
![]() )
называется образом
пространства
R
при преобразовании A
(другими
словами образ – множество векторов y,
для которых уравнение Ax=y
имеет хотя бы одно решение).
)
называется образом
пространства
R
при преобразовании A
(другими
словами образ – множество векторов y,
для которых уравнение Ax=y
имеет хотя бы одно решение).
1) Находим ядро.
Пусть
![]() - вектор столбец. Решаем систему уравнений
- вектор столбец. Решаем систему уравнений
 .
.
Решаем систему методом Гаусса
 .
.
Переменные
![]() - базисные, а
- базисные, а
![]() - небазисная.
- небазисная.
Находим все
фундаментальные решения. В нашем случае
оно одно: положив
![]() ,
получаем
,
получаем
![]() - который и будет образовывать базис
ядра (т.к. все вектора вида
- который и будет образовывать базис
ядра (т.к. все вектора вида
![]() отображаются в 0). Размерность базиса
равна 1.
отображаются в 0). Размерность базиса
равна 1.
2) Находим образ. Пусть - вектор столбец. Решаем систему уравнений Ax=y.
Для того, чтобы
вектор
![]() принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:
принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:
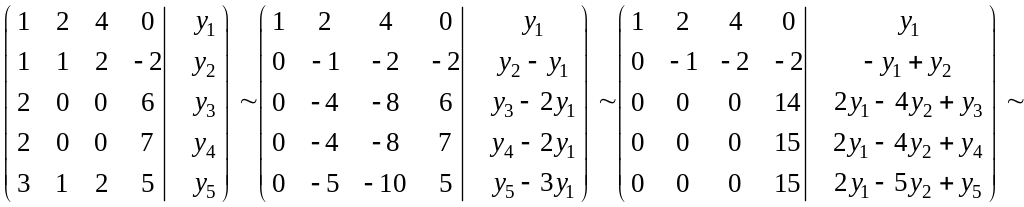
 .
.
Т.к. rang(A) = 3, то для того чтобы rang(A|y) =2, необходимо и достаточно, чтобы
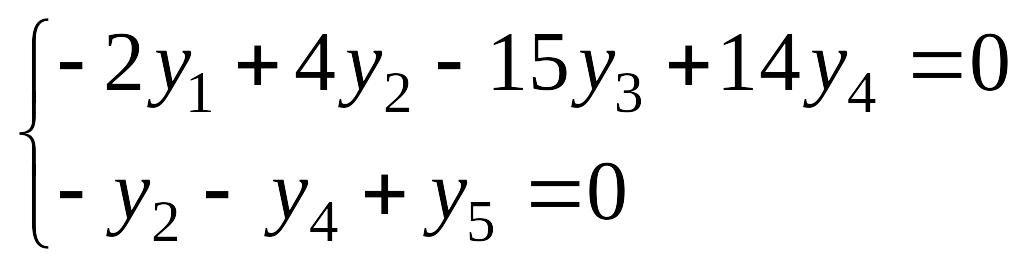 .
.
Находим фундаментальные
решения (базис образа). Т.к. определитель
из коэффициентов при
![]() :
:
![]() ,
то
,
то
![]() - базисные, а
- базисные, а
![]() - небазисные.
- небазисные.
1-е фундаментальное
решение. Положим
![]() ,
находим решение системы
,
находим решение системы
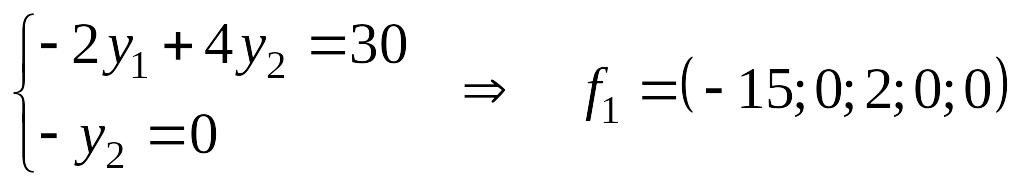 - первое базисное
решение.
- первое базисное
решение.
2-е фундаментальное
решение. Положим
![]() ,
находим решение системы
,
находим решение системы
 - второе базисное
решение.
- второе базисное
решение.
3-е фундаментальное
решение. Положим
![]() ,
находим решение системы
,
находим решение системы
 - второе базисное
решение.
- второе базисное
решение.
Итак, размерность
образа равна 3, базис – вектора
![]() .
.
(Видно, что размерность образа + размерность ядра = размерности пространства R4).
7. Найти размерность пространства и , где , а м – пространство решений системы уравнений .
Решение.
![]() - ядро,
- ядро,
![]() - образ. Преобразование
- образ. Преобразование
![]() .
.
1) Находим ядро. Решаем систему уравнений

Следовательно,
одно базисное решение
![]() - базис ядра. Размерность
- базис ядра. Размерность
![]() .
.
2) Находим образ.
Пусть
![]() - вектор столбец. Решаем систему уравнений
Ax=y.
- вектор столбец. Решаем систему уравнений
Ax=y.
Для того, чтобы
вектор
![]() принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:
принадлежал образу, необходимо и
достаточно, чтобы ранг матрицы А, и ранг
расширенной матрицы (A|y)совпадали.
Если теперь с помощью эквивалентных
преобразований привести (A|y)
к ступенчатому виду, то получим:
 .
.
Т.к. rang(A) = 2, то для того чтобы rang(A|y) =2, необходимо и достаточно, чтобы
![]()
Отсюда,
![]() -
базисная, а
-
базисная, а
![]() не базисные переменные.
не базисные переменные.
1-е фундаментальное
решение:
![]() .
.
2-е фундаментальное
решение:
![]() .
.
Следовательно,
![]() - базис образа. Размерность
- базис образа. Размерность
![]() .
.
3) Находим
ортогональное дополнение
![]() .
Т.к. любой вектор
.
Т.к. любой вектор
![]() ,
перпендикулярен любому вектору из
,
то заключаем, что скалярное произведение
,
перпендикулярен любому вектору из
,
то заключаем, что скалярное произведение
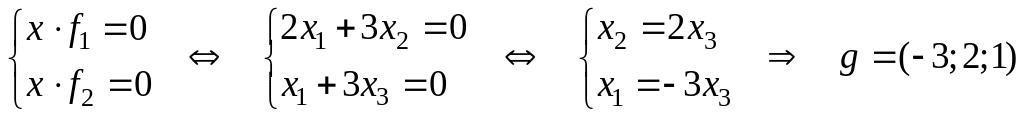 - фундаментальное
решение системы или базис
- фундаментальное
решение системы или базис
![]() .
.
4) Найдем базис
линейной оболочки векторов
![]() ,
,
![]() .
Т.к.
.
Т.к.
 ,
то заключаем, что
,
- базис в
,
и следовательно, размерность
,
то заключаем, что
,
- базис в
,
и следовательно, размерность
![]() .
.
5) Находим пространство решений системы уравнений .
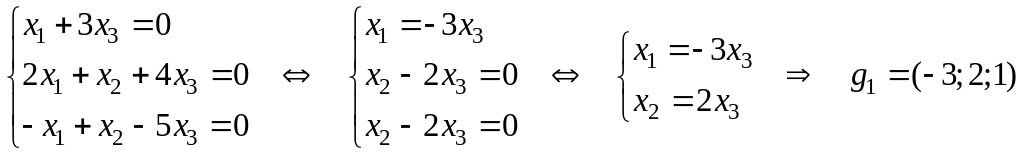 - фундаментальное
решение системы или базис M.
- фундаментальное
решение системы или базис M.
6) Находим
ортогональное дополнение
![]() .
Т.к. любой вектор
.
Т.к. любой вектор
![]() ,
перпендикулярен любому вектору из
,
перпендикулярен любому вектору из
![]() ,
то заключаем, что скалярное произведение
,
то заключаем, что скалярное произведение
![]() .
.
Отсюда,
![]() -
базисная, а
-
базисная, а
![]() не базисные переменные.
не базисные переменные.
1-е фундаментальное
решение:
![]() .
.
2-е фундаментальное
решение:
![]() .
.
Следовательно,
![]() - базис
.
Размерность
- базис
.
Размерность
![]() .
.
7) Найдем базис линейной оболочки векторов , , , .
Очевидно, что
![]() ,
а
,
- базис в
,
и следовательно, размерность
,
а
,
- базис в
,
и следовательно, размерность
![]() .
.
8. Пусть U
- подпространство
линейного пространства R4,
являющееся линейной оболочкой. векторов
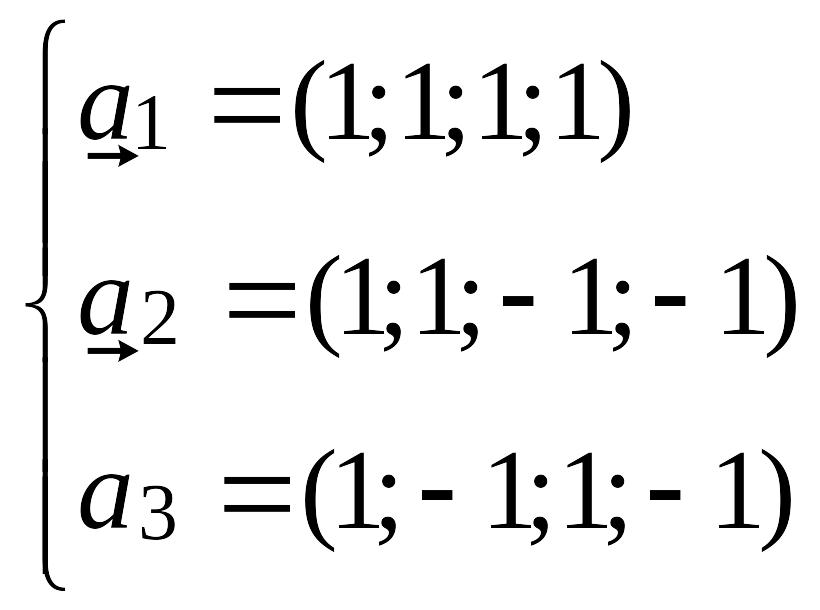 ,
V
- подпространство
линейного пространства R4
являющееся
линейной оболочкой векторов
,
V
- подпространство
линейного пространства R4
являющееся
линейной оболочкой векторов
 .
Найдите: базис U
+ V
и
базис
.
Найдите: базис U
+ V
и
базис
![]() .
.
Решение.
1) Находим базис в U.
 rang=3
, сл-но,
rang=3
, сл-но,
![]() - базис U.
- базис U.
1) Находим базис в V.
 rang=3
, сл-но,
rang=3
, сл-но,
![]() - базис V.
- базис V.
3) Находим базис в U + V.
Находим линейно
независимые вектора в объединении
![]() .
.

![]() ,
а вектора
,
а вектора
![]() - базис U
+ V
, а размерность
dim(U
+ V)=4.
- базис U
+ V
, а размерность
dim(U
+ V)=4.
4) Найдем общие вектора в U и V .
Нам известно, что в конечномерном пространстве подпространства могут быть заданы системами линейных уравнений. Тогда их пересечение задаётся системой уравнений, полученной объединением систем, задающих подпространства.
Система уравнений задающая U:
Для того, чтобы вектор принадлежал линейной оболочке U, необходимо и достаточно, чтобы ранг матрицы А и ранг расширенной матрицы (A|y)совпадали. Если теперь с помощью эквивалентных преобразований привести (A|y) к ступенчатому виду, то получим:

Т.к. rang(A) = 3, то для того чтобы rang(A|y) =3, необходимо и достаточно, чтобы
![]() - искомая система
линейных уравнений.
- искомая система
линейных уравнений.
Система уравнений задающая V:
Для того, чтобы вектор принадлежал линейной оболочке U, необходимо и достаточно, чтобы ранг матрицы А и ранг расширенной матрицы (A|y)совпадали. Если теперь с помощью эквивалентных преобразований привести (A|y) к ступенчатому виду, то получим:
 Т.к.
rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы
Т.к.
rang(A)
= 3, то для того чтобы rang(A|y)
=3, необходимо и достаточно, чтобы
![]() - искомая система
линейных уравнений.
- искомая система
линейных уравнений.
Решаем общую систему:
 .
.
Отсюда фундаментальные
решения (которые получаются при
![]() и при
и при
![]() ),
а следовательно базис
есть:
),
а следовательно базис
есть:
![]() .
.
9. Подпространство
L1
в R4
порождено векторами (1;-4;6;7) и (0;1;-3;1), а
подпространство L2
- векторами
(0;1;-4;5) и (1;-4;7;-11). Постройте базисы следующих
подпространств: пересечения
![]() и ортогонального дополнения к сумме
и ортогонального дополнения к сумме
![]() .
.
Решение.
1) Находим базис в
L1.
Т.к. матрица, составленная из координат
векторов
![]() ,
имеет ранг=2 (т.к. в ней есть определитель
второго порядка
,
имеет ранг=2 (т.к. в ней есть определитель
второго порядка
![]() ),
то заключаем, что вектора
),
то заключаем, что вектора
![]() =(1;-4;6;7)
и
=(1;-4;6;7)
и
![]() =(0;1;-3;1)
линейно независимые и образуют базис
в L1.
=(0;1;-3;1)
линейно независимые и образуют базис
в L1.
2) Аналогично,
заключаем, что вектора
![]() =(0;1;-4;5)
и
=(0;1;-4;5)
и
![]() =(1;-4;7;-11)
линейно независимые и образуют базис
в L2.
=(1;-4;7;-11)
линейно независимые и образуют базис
в L2.
3) Находим базис L1+ L2.
Рассматриваем объединенную систему векторов
=(1;-4;6;7), =(0;1;-3;1), =(0;1;-4;5), =(1;-4;7;-11)
и находим среди
них линейно независимые. Находим ранг
матрицы, столбцами которой являются
координаты
![]() :
:
 .
.
Ранг = 4, следовательно, все вектора - линейно независимые и образуют базис в L1+ L2.
4) Находим базис ортогонального дополнения .
Каждый вектор из
![]() ортогонален любому вектору из L1+
L2.
Следовательно, скалярные произведения
на вектора базиса из L1+
L2
равны 0. Получаем однородную систему
ортогонален любому вектору из L1+
L2.
Следовательно, скалярные произведения
на вектора базиса из L1+
L2
равны 0. Получаем однородную систему
![]() .
.
Т.к. определитель
системы не равен 0 (показано выше, что
ранг=4), то система имеет единственное
тривиальное решение
![]() .
.
Следовательно,
состоит
только из одного вектора
![]() .
.
(Это и так было
видно, т.к. линейная оболочка
![]() ,
ибо 4 линейно независимых вектора
образуют базис в
,
ибо 4 линейно независимых вектора
образуют базис в
![]() ,
а
,
а
![]() ).
).
5) Находим систему уравнений описывающую L1.
Для того, чтобы вектор принадлежал линейной оболочке , необходимо и достаточно, чтобы ранг матрицы А – составленной из координат векторов , и ранг расширенной матрицы (A|y)совпадали. Если теперь с помощью эквивалентных преобразований привести (A|y) к ступенчатому виду, то получим:
 .
.
Т.к. rang(A) = 2, то для того чтобы rang(A|y) =2, необходимо и достаточно, чтобы
![]() - искомая система
линейных уравнений.
- искомая система
линейных уравнений.
Находим систему уравнений описывающую L2.
Для того, чтобы вектор принадлежал линейной оболочке , необходимо и достаточно, чтобы ранг матрицы А – составленной из координат векторов , и ранг расширенной матрицы (A|y)совпадали. Если теперь с помощью эквивалентных преобразований привести (A|y) к ступенчатому виду, то получим:
 .
.
Т.к. rang(A) = 2, то для того чтобы rang(A|y) =2, необходимо и достаточно, чтобы
![]() - искомая система
линейных уравнений.
- искомая система
линейных уравнений.
Решаем общую систему:
![]() Т.к. определитель
матрицы коэффициентов
Т.к. определитель
матрицы коэффициентов
![]() ,
то система имеет единственное решение
,
то система имеет единственное решение
![]() .
Следовательно,
состоит из
одного вектора (0;0;0;0).
.
Следовательно,
состоит из
одного вектора (0;0;0;0).
(Это и так было
видно, т.к. вектора
- линейно независимые,
линейные оболочки
![]() и
и
![]() не имеют общих (кроме нулевого) векторов,
т.к. линейная комбинация векторов
не имеют общих (кроме нулевого) векторов,
т.к. линейная комбинация векторов
![]() не может дать вектора
не может дать вектора
![]() ,
а следовательно и их линейные комбинации).
,
а следовательно и их линейные комбинации).
