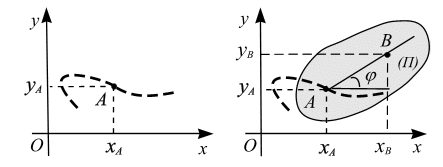Правила интегрирования

Неопределенный интеграл:

, где , .

Свойства неопределенного интеграла:

; .

Свойство линейности:

.

Метод замены переменной:

, где .

Метод интегрирования по частям

.

Свойства определенного интеграла:

; ;

;

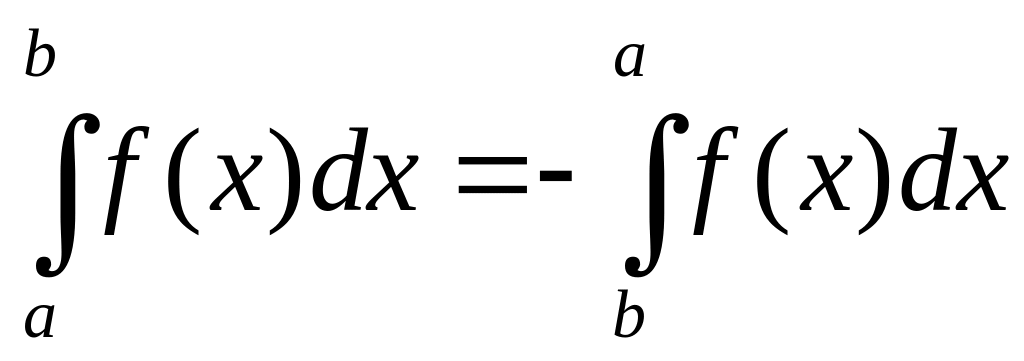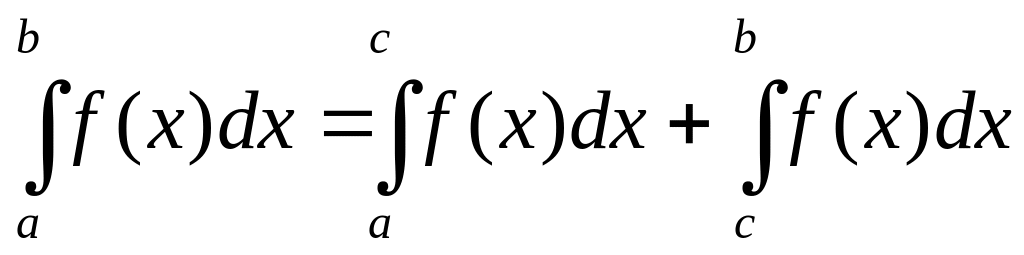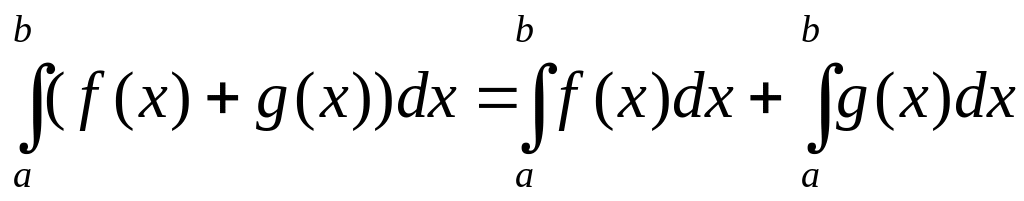Формула Ньютона – Лейбница:

.

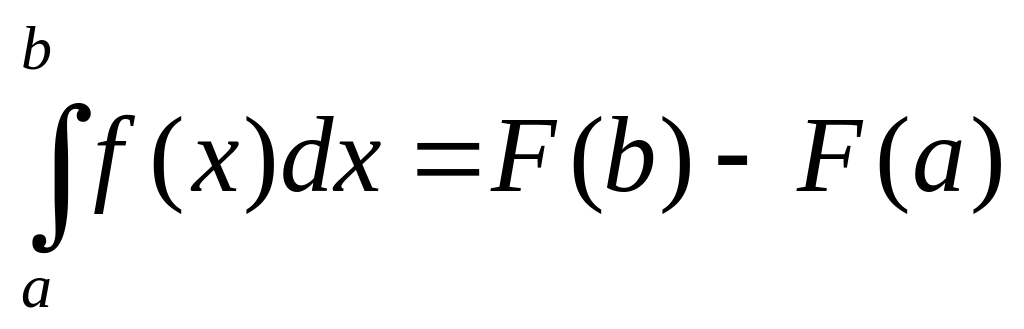Справедливость ниже указанных формул легко проверить дифференцированием.

Таблица интегралов

1		9
2		10
3		11
4		12
5		13
6		14
7		15
8		16

1.6. Понятие об абсолютно твердом теле и его степенях свободы

Важным понятием в механике является число параметров, полностью определяющих положение всех точек рассматриваемой системы, в частности твердого тела. Эти параметры носят название степеней свободы.

Свободным называется тело, на перемещения точек которого не наложено никаких ограничений. Вычислим количество степеней свободы твердого тела в плоскости и пространстве.

Число независимых параметров, определяющих перемещение тела (точек тела) на плоскости или в пространстве называется числом его степеней свободы.

Плоскость. Положение точки на плоскости в системе координат определяется двумя независимости параметрами (координатами) – (рис. 1.19, а), т. е. точка может независимо перемещаться в двух ортогональных направлениях и , следовательно, точка имеет две степени свободы.

а	б
Рис. 1.19

Положение твердого тела характеризовать двумя параметрами не получится, необходимо зафиксировать еще одну точку, тогда положение твердого тела на плоскости будет определено четырьмя параметрами – координатами двух точек – и (рис.1.19, б).

Предположим, что при движении или взаимодействии с другими телами твердое тело не меняет своей геометрической формы, тогда расстояние между точками А и В будет оставаться неизменным:

Такие твердые тела называют абсолютно твердыми. В теоретической механике реальные тела моделируются абсолютно твердыми телами.

Абсолютно твердым телом (или неизменяемой механической системой) называют твердое тело, расстояние между любыми точками которого не меняется при его движении и взаимодействии с другими телами.

Тогда четыре координаты , , определяющие положение абсолютно твердого тела, связаны между собой теоремой Пифагора:

. (1.1)

Это уравнение принято называть уравнением связи. Тогда из четырех координат , независимые только три:

4 Координаты – 1 уравнение связи 3 независимых координаты.

Поэтому движение абсолютно твердого тела в плоскости должно описываться тремя независимыми параметрами. За независимые параметры принимают координаты любой точки А – (часто центра тяжести тела) и угол , который образуют жестко связанная с телом прямая АВ и положительное направление оси (рис. 1.19, б). Итак, положение абсолютно твердого тела в плоскости будет определяться тремя независимыми параметрами – ,  и, следовательно, твердое тело при движении в плоскости будет иметь три степени свободы: тело может перемещаться вдоль каждой из осей и вращаться вокруг точки А. Точку А называют полюсом.

Число независимых перемещений тела определяет число его степеней свободы

Абсолютно твердое тело в плоскости имеет три степени свободы.

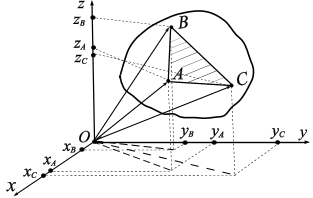
Пространство. Одна свободная точка в пространстве имеет три степени свободы. Рассмотрим свободное абсолютно твердое тело в пространстве (рис. 1.20). Положение твердого тела характеризовать двумя точками А и В в пространстве не получится, потому что тело может вращаться вокруг прямой АВ, при этом координаты точек А и В меняться не будут. Необходимо зафиксировать еще одну точку, тогда положение тела в пространстве будет определяться заданием координат трех его точек, не лежащих на одной прямой  , , . Положение тела в пространстве в декартовой системе координат будет характеризоваться девятью параметрами. Поскольку взаимное расположение точек А, В и С абсолютно твердого тела сохраняется (рис. 1.20), девять координат связаны между собой тремя уравнениями связи:

– расстояние АВ;

– расстояние АС;

– расстояние ВС.

	На девять координат наложено три уравнения связи, следовательно, независимых координат остается только шесть, т. е. абсолютно твердое тело в пространстве имеет шесть степеней свободы: тело может независимо перемещаться вдоль каждой из осей и вращаться вокруг
Рис. 1.20

каждой оси. За независимые параметры принимают координаты полюса А – и углы поворота плоскости АВС вокруг каждой из осей, т. е. точка может независимо перемещаться в трех ортогональных направлениях .

Если при движении или взаимодействии с другими телами твердое тело меняет свою геометрическую форму (деформируется), тогда расстояние между двумя точками не будет оставаться неизменным, т. е. координаты точек не связаны между собой. В этом случае будем говорить о деформируемом твердом теле.