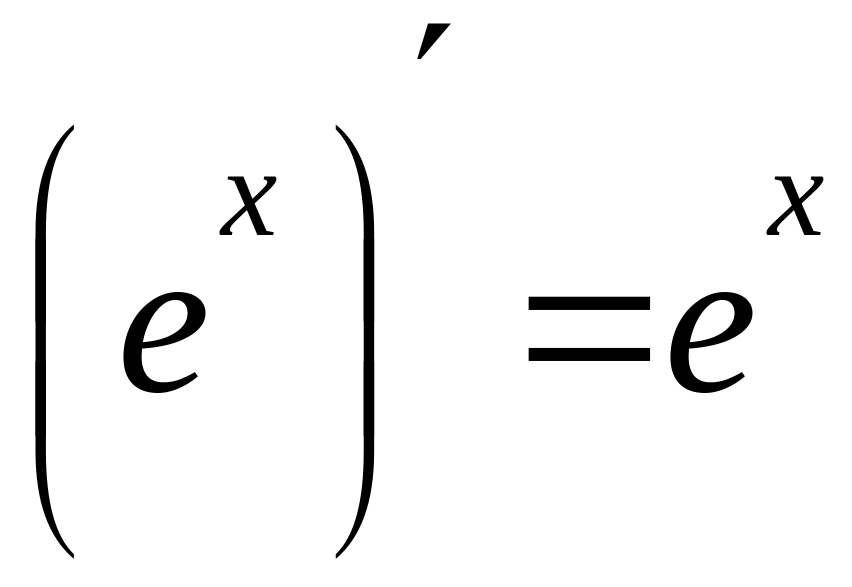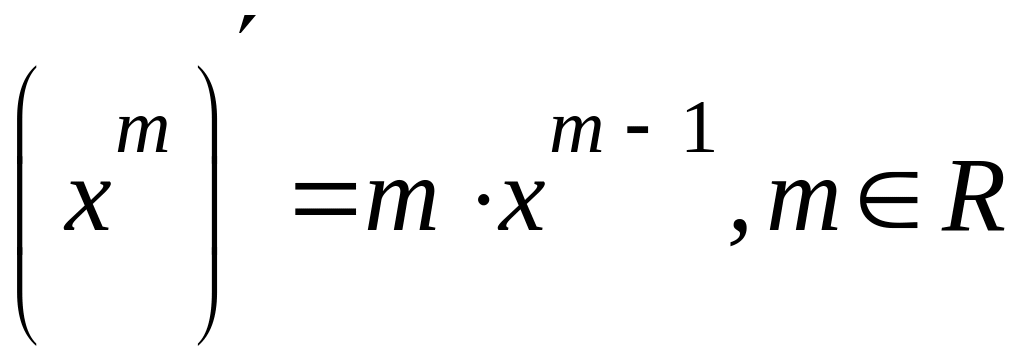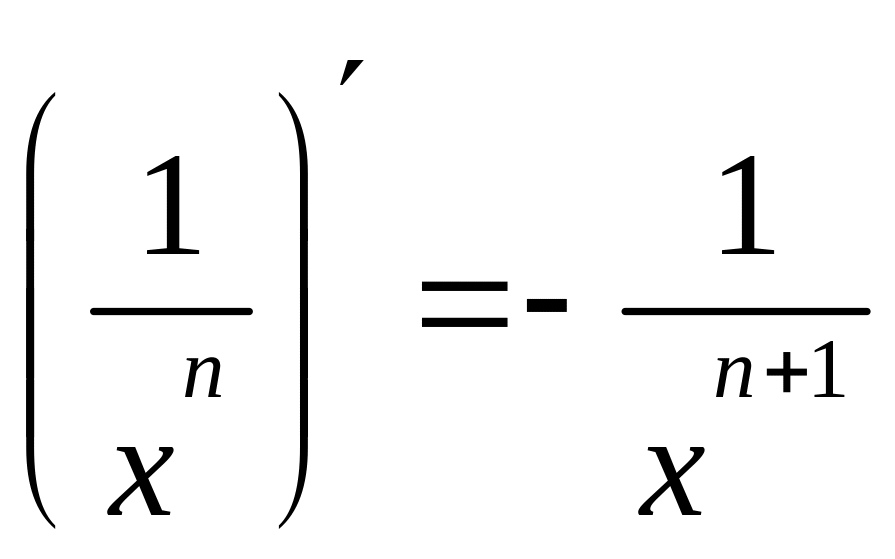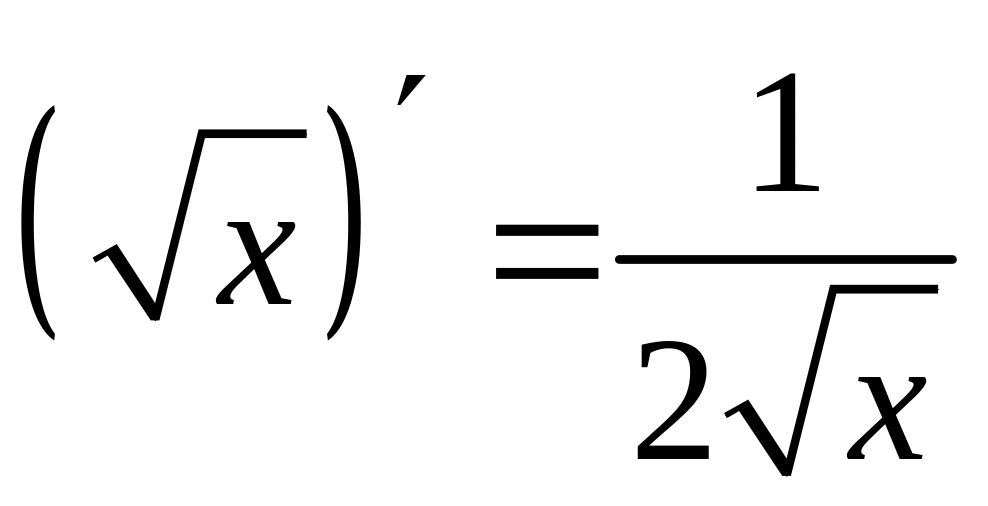- •Введение
- •Общие указания
- •Модуль 2. Статика
- •Основны математического аппарата
- •Прямоугольная декартова система координат
- •Графики аналитических функций в декартовой системе координат
- •Элементы тригонометрии
- •Графики тригонометрических функций
- •График функции представлен на рис. 1.9; это кривая называется также синусоидой, полученная в результате перемещения графика вдоль оси х влево на /2.
- •Векторы
- •Основы математического анализа
- •Правила интегрирования
- •1.6. Понятие об абсолютно твердом теле и его степенях свободы
- •4 Координаты – 1 уравнение связи 3 независимых координаты.
- •1.7. Инерциальная система отсчета
- •Кинематика
- •2.1. Траектория, скорость, ускорение материальной точки
- •Вращение твердого тела относительно неподвижной точки в плоскости
- •Сложное движение точки
- •2.4. Плоскопараллельное движение твердого тела
- •3. Статика
- •3.1. Основные элементы статики
- •3.2. Плоские фермы. Способы расчета
- •3.3. Принципы расчета составных конструкций
- •Общие указания по выполнению и оформлению контрольных работ.
- •Контрольные работы Контрольная работа № 1
- •Контрольная работа № 2. Плоское движение твердого тела Задача 1. Кинематический анализ плоского механизма
- •Контрольная работа №3. Плоская система сил
- •Библиографический список Основной
- •Дополнительный
- •Оглавление
- •660041, Г. Красноярск, пр. Свободный, 79
- •660041, Г. Красноярск, пр. Свободный, 82а
Основы математического анализа
Дифференцирование
функций.
Для решения многих задач требуется
найти разность значений функции в двух
точках. Так, средняя скорость материальной
точки за промежуток времени Δt
равна
![]() .
Если рассматриваемое движение не
является равномерным, то чем меньше
выбран промежуток времени Δt,
тем лучше указанная формула будет
характеризовать движение точки. В идеале
мы получаем понятие мгновенной скорости
.
Если рассматриваемое движение не
является равномерным, то чем меньше
выбран промежуток времени Δt,
тем лучше указанная формула будет
характеризовать движение точки. В идеале
мы получаем понятие мгновенной скорости
![]() :
это предел, к которому стремится средняя
скорость, когда t → 0,
то есть
:
это предел, к которому стремится средняя
скорость, когда t → 0,
то есть
![]()
Эта и другие задачи приводят к понятию производной.
Пусть
функция y = f (x)
определена в некоторой окрестности
точки
![]() и
существует
и
существует
![]() конечный предел отношения при Δx → 0.
Тогда этот предел называется производной
функции в точке
:
конечный предел отношения при Δx → 0.
Тогда этот предел называется производной
функции в точке
:
![]() .
.
Производная
функции y = f (x)
может также обозначаться одним из
следующих способов:
![]()
Г
Рис.
1.17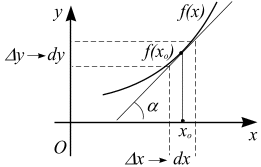
![]() .
где
.
где
![]() – угол между осью
и касательной к кривой в данной точке
,
отчитываемый от положительного
направления оси
против часовой стрелки. В механике
производную по времени t
часто обозначают точкой:
– угол между осью
и касательной к кривой в данной точке
,
отчитываемый от положительного
направления оси
против часовой стрелки. В механике
производную по времени t
часто обозначают точкой:
![]() .
.
Если приращение функции f (x0 + Δx) – f (x0) обозначить как Δy, то определение можно записать так:
![]() .
.
Линейную
функцию
![]() называют дифференциалом функции f
в
точке
и обозначают df.
Для функции x
производная в каждой точке
равна 1, то есть
называют дифференциалом функции f
в
точке
и обозначают df.
Для функции x
производная в каждой точке
равна 1, то есть
![]() .
.
Поэтому пишут:
![]() .
.
Геометрически
дифференциал функции
![]() – это приращение ординаты касательной
к графику функции в данной точке при
изменении абсциссы точки на dx
(рис.
1.17).
– это приращение ординаты касательной
к графику функции в данной точке при
изменении абсциссы точки на dx
(рис.
1.17).
Операция вычисления производной называется дифференцированием. Функция называется дифференцируемой в данной точке, если в этой точке существует ее производная.
Таблица производных
1 |
|
7 |
|
13 |
|
2 |
|
8 |
|
14 |
|
3 |
|
9 |
|
15 |
|
4 |
|
10 |
|
16 |
|
5 |
|
11 |
|
17 |
|
6 |
|
12 |
|
18 |
|
И
Рис.
1.18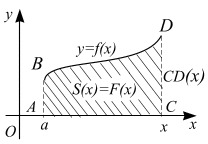
![]() ,
определенной в некоторой области
,
определенной в некоторой области
![]() ,
называется такая функция
,
называется такая функция
![]() ,
определенная в той же области, производная
от которой равна
,
определенная в той же области, производная
от которой равна
![]() .
.
Геометрический
смысл первообразной. Если
данная функция
изображена кривой в декартовых
координатах, то первообразная численно
равна площади
![]() ,
ограниченной кривой
,
осью
и двумя ординатами: постоянной АВ
(при
,
ограниченной кривой
,
осью
и двумя ординатами: постоянной АВ
(при
![]() )
и переменной
)
и переменной
![]() (при абсциссе
(при абсциссе
![]() ).
Произвольно выбирая постоянную а,
получаем
различные первообразные. При этом
площадь
понимается в алгебраическом смысле
(рис.1.18):
).
Произвольно выбирая постоянную а,
получаем
различные первообразные. При этом
площадь
понимается в алгебраическом смысле
(рис.1.18):
площадь
фигуры АВСD
=
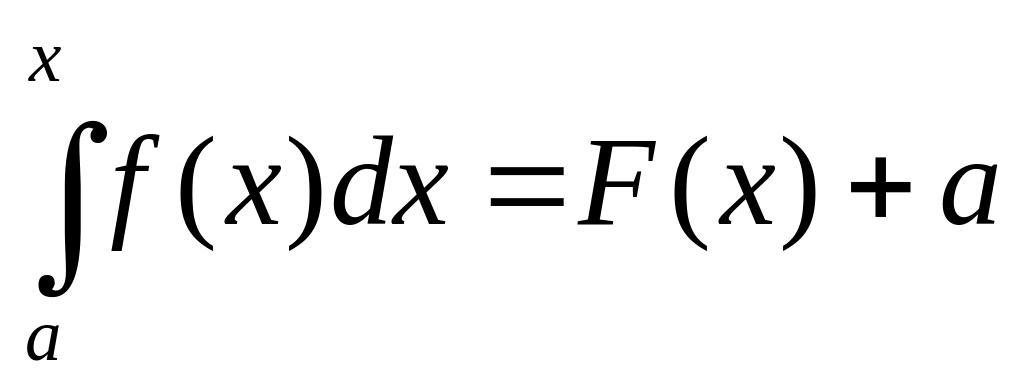 .
.
Процесс нахождения первообразной называется интегрированием.
Интегрирование является операцией, обратной дифференцированию.