- •Введение
- •Общие указания
- •Модуль 2. Статика
- •Основны математического аппарата
- •Прямоугольная декартова система координат
- •Графики аналитических функций в декартовой системе координат
- •Элементы тригонометрии
- •Графики тригонометрических функций
- •График функции представлен на рис. 1.9; это кривая называется также синусоидой, полученная в результате перемещения графика вдоль оси х влево на /2.
- •Векторы
- •Основы математического анализа
- •Правила интегрирования
- •1.6. Понятие об абсолютно твердом теле и его степенях свободы
- •4 Координаты – 1 уравнение связи 3 независимых координаты.
- •1.7. Инерциальная система отсчета
- •Кинематика
- •2.1. Траектория, скорость, ускорение материальной точки
- •Вращение твердого тела относительно неподвижной точки в плоскости
- •Сложное движение точки
- •2.4. Плоскопараллельное движение твердого тела
- •3. Статика
- •3.1. Основные элементы статики
- •3.2. Плоские фермы. Способы расчета
- •3.3. Принципы расчета составных конструкций
- •Общие указания по выполнению и оформлению контрольных работ.
- •Контрольные работы Контрольная работа № 1
- •Контрольная работа № 2. Плоское движение твердого тела Задача 1. Кинематический анализ плоского механизма
- •Контрольная работа №3. Плоская система сил
- •Библиографический список Основной
- •Дополнительный
- •Оглавление
- •660041, Г. Красноярск, пр. Свободный, 79
- •660041, Г. Красноярск, пр. Свободный, 82а
Прямоугольная декартова система координат
а
|
Р |
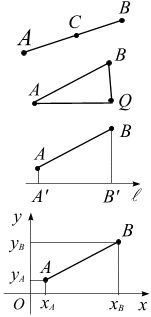
Наиболее
элементарными измерениями в механике,
кроме простого счета, являются измерения
расстояний. Расстояние вдоль заданной
прямой АВ
аддитивно, т. е. его можно представить
в виде алгебраической суммы двух
расстояний
|
б |
||
в |
||
г |
Рене
Декарт предложил задавать положение
точек отрезка с помощью системы
параллельных отрезков
![]() и
и
![]() ,
перпендикулярных к исходной прямой
,
перпендикулярных к исходной прямой
![]() .
В дальнейшем была введена вторая ось,
перпендикулярная первой. Система двух
ортогональных осей получила название
декартовой системы координат (рис. 1.1,
в).
.
В дальнейшем была введена вторая ось,
перпендикулярная первой. Система двух
ортогональных осей получила название
декартовой системы координат (рис. 1.1,
в).
Декартова плоская система координат задается двумя взаимно перпендикулярными прямыми осями координат, на каждой из которых выбрано положительное направление и задан отрезок единичной длины. Точка пересечения осей координат (О) называется началом координат. Одна из осей координат (Ох ) называется осью абсцисс, другая – осью ординат (Оу).
Расстояние между точками А и В определяется по теореме Пифагора:
![]() .
.
Декартова
система координат в трехмерном
пространстве задается аналогично случаю
плоскости: осью абсцисс (![]() ),
осью ординат (
),
осью ординат (![]() ),
осью аппликат (
),
осью аппликат (![]() )
и началом координат О
(рис.
1.2).
)
и началом координат О
(рис.
1.2).
Возможны
две прямоугольные декартовы системы
координат, которые никакими движениями
в пространстве не могут быть совмещены
друг с другом. Одна из них правая, другая
– левая. Наиболее употребляемой системой
координат является правая (рис. 1.2, а).
Систему координат свяжем с поверхностью
земли. Пусть наблюдатель стоит на земле
лицом на север, правая его рука направлена
на восход солнца, т. е. на восток. Совместим
с наблюдателем систему трех ортогональных
осей
![]() с поверхностью земли, при этом ось
с поверхностью земли, при этом ось
![]() направим на север, ось
направим на север, ось
![]() будет указывать вместе с правой рукой
на восток, ось
будет указывать вместе с правой рукой
на восток, ось
![]() направим вертикально на звезды.
направим вертикально на звезды.
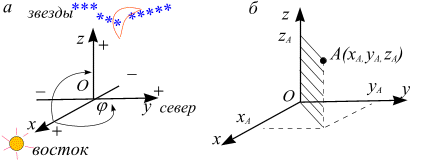
Рис. 1.2
Такая система называется правой декартовой системой координат. В правой системе координат поворот оси Оx в плоскости Оxy и в плоскости Оxz против часовой стрелки считается положительным, по часовой стрелке – отрицательным.
Р |
Положение
геометрической точки А
в
декартовой системе координат определено
тремя независимыми координатами:
Положение
геометрической точки А
в плоской системе координат определено
двумя независимыми координатами –
|
Графики аналитических функций в декартовой системе координат
Элементарные функции функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
Линейная функция.
Если переменные y и x пропорциональны, то функциональная зависимость между ними выражается уравнением
![]() ,
,
где k – постоянная величина (коэффициент пропорциональности).
График
прямой
пропорциональности
– прямая линия, проходящая через начало
координат и образующая с осью X
угол ,
причем
![]() –
коэффициент пропорциональности или
угловой
коэффициент.
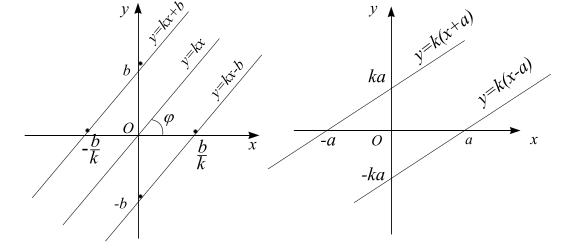
На рис. 1.4 показаны графики линейных
функций.
–
коэффициент пропорциональности или
угловой
коэффициент.
На рис. 1.4 показаны графики линейных
функций.
|
Рис. 1.4 |
Квадратичная функция: y = ax2 + bx + c, где
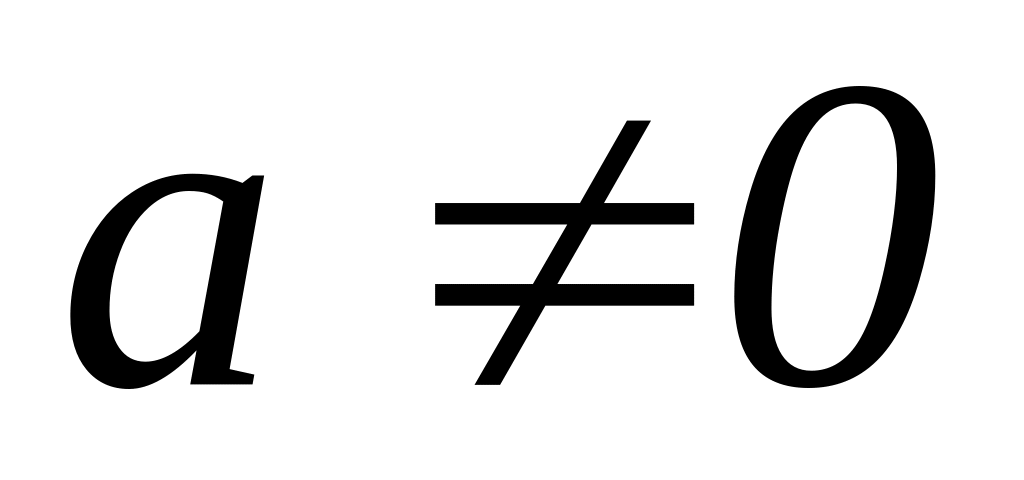 .
.
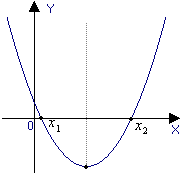
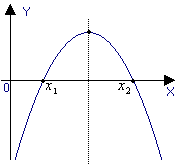
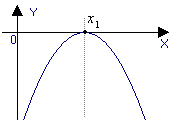
График квадратичной функции парабола.
Свойства функции и вид её графика определяются в основном значениями коэффициента a и дискриминанта D = b2 4ac (рис. 1.5).
Нули
квадратичной функции:
при D
> 0 существует два нуля:
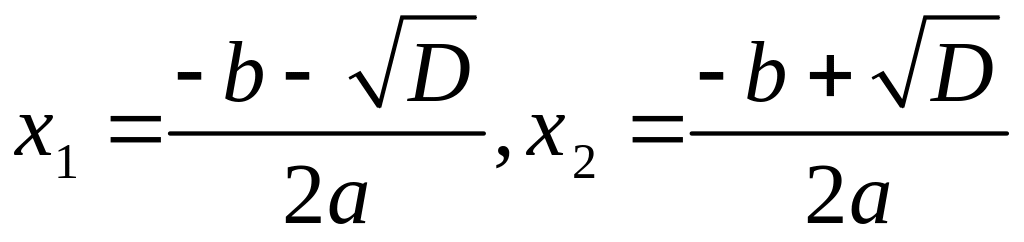 ;
при D
= 0 существует один нуль: x1
= b/(2a)
, при D
< 0 нулей нет.
;
при D
= 0 существует один нуль: x1
= b/(2a)
, при D
< 0 нулей нет.
a > 0, D > 0 |
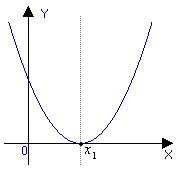
a > 0, D = 0 |
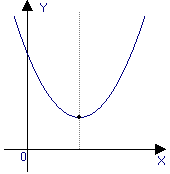
a > 0, D < 0 |
|
|
|
a < 0, D > 0 |
a < 0, D = 0 |
a < 0, D < 0 |
|
|
|
Рис. 1.5
Разложение на линейные множители:
при D > 0 y = ax2 + bx + c = a(x x1)(x x2),
при D = 0 y = ax2 + bx + c = a(x x1)2 ,
при D < 0 функцию разложить на множители нельзя.
Выделение полного квадрата:
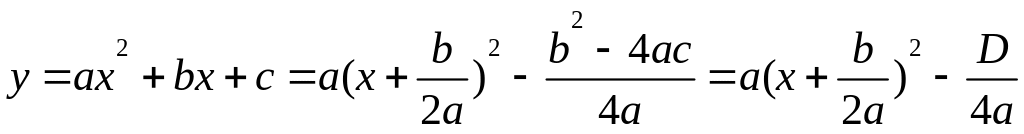 .
.
Квадратичная функциональная зависимость. Алгебраическая функция вида
![]() ,
,
где А, B, C, D, E, F действительные числа, называется функциональной зависимостью второй степени (порядка) или квадратичной функциональной зависимостью (кривые второго порядка). Графиками этой зависимости во множестве действительных чисел могут быть или окружности, или эллипсы, или параболы, или гиперболы.
Окружность. Каноническое (простейшие) уравнение окружности (рис.1.6, а):
![]() ;
;
параметрическое задание окружности:
![]()
Эллипс. Каноническое уравнение эллипса (рис.1.6, б):
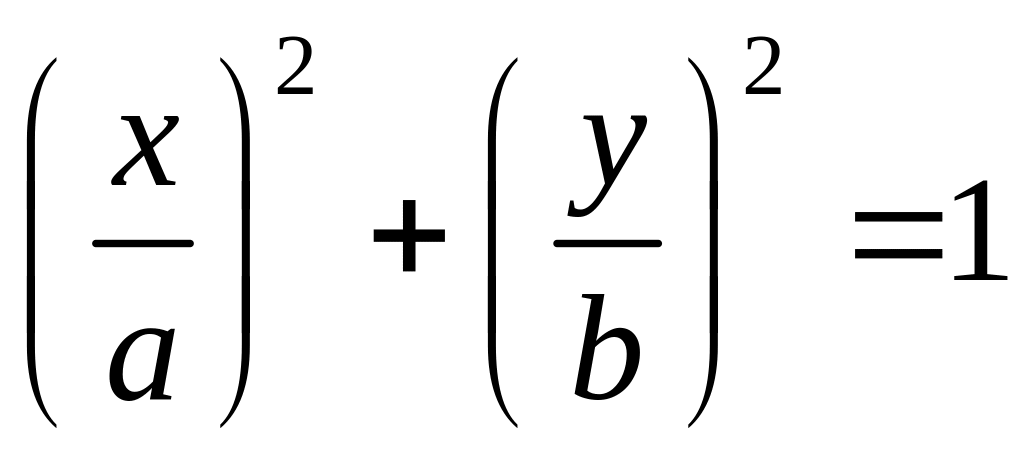 .
.
Параметрическое задание эллипса:
![]()
Графики окружности и эллипса представлены на рис. 1.6, а, б.
-

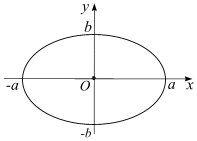
а
б
Рис. 1.6

 ис.
1.1
ис.
1.1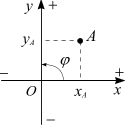 ис.
1.3
ис.
1.3