2. Сложное движение точки

Движение точки по отношению к двум или нескольким системам отсчета называется сложным. Движение точки М по отношению к подвижной системе отсчета называется относительным (рис. 2.16). Используются понятия: относительная траектория, относительная скорость ( ) и относительное ускорение ( ).

Рис. 2.16

Движение подвижной системы отсчета по отношению к неподвижной является для точки переносным. Скорость и ускорение точки подвижной системы отсчета, в которой в данный момент времени находится движущаяся точка М, называются переносной скоростью ( ) и переносным ускорением ( ).

Движение точки М по отношению к неподвижной системе отсчета называется сложным или абсолютным. Используются понятия: абсолютная траектория, абсолютная скорость ( ) и абсолютное ускорение ( ).

Теорема. Абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей:

,

здесь: скорость относительного движения;

– скорость переносного движения.

Теорема. Абсолютное ускорение точки равно геометрической сумме трёх ускорений – относительного, переносного и ускорения Кориолиса (или поворотного):

,

здесь: – ускорение относительного движения;

– переносное ускорение;

– ускорение Кориолиса.

Ускорение Кориолиса ( ) равно удвоенному векторному произведению угловой скорости переносного вращения ( ) на относительную скорость точки ( ):

Модуль ускорения Кориолиса равен

.

Здесь: угол , угол между вектором относительной скорости и вектором угловой скорости переносного вращения .

Направление ускорения Кориолиса определяется по правилу Жуковского.

Правило Жуковского (рис. 2.17):

1. С

   

   Рис. 2.17

   ледует провести плоскость перпендикулярно оси переносного вращения ( ).

2. Спроецировать вектор относительной скорости на эту плоскость: .

3. Повернуть эту проекцию в этой плоскости на 90⁰ по направлению дуговой стрелки переносного вращения .

Содержание контрольных работ для студентов на тему «сложное движение точки» дано в приложении (контрольная работа 1, задача 3).

П

Рис. 2.18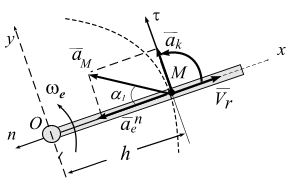

ример 2.4. Стержень вращается в плоскости вокруг неподвижного центра в плоскости рисунка с постоянной угловой скоростью . Точка М скользит вдоль стержня со скоростью . Вычислить абсолютное ускорение точки для момента времени 4 с (рис. 2.18).

Решение. Стержень вращается в плоскости вокруг неподвижного центра с угловой скоростью с^–1. Точка М скользит вдоль стержня со скоростью (рис. 2.18). Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.

,

здесь: вектор относительного ускорения , т. к.

Вектор переносного ускорения

,

где , ,

здесь см.

вектор направлен по оси .

Ускорение Кориолиса ,

при

.

Определим направление вектора , используя правило Жуковского. Угол между вектором относительной скорости и равен (вектор ), тогда вектор разворачиваем на по направлению дуговой стрелки (рис. 2.18).

Вычислим абсолютное ускорение точки :

Тангенс угла (₁) между и осью равен:

.

В момент времени ,

,

.

Ответ: а_М = 2,83 см/с².

Пример 2.5. Пластина В вращается вокруг неподвижной оси согласно уравнению (рис. 2.19). На пластине по желобу движется точка согласно уравнению

см.

В

Рис. 2.19

ычислить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1 с, если радиус желоба .

Решение. Будем считать, что в момент времени t = 1 с угол поворота имеет такое значение, при котором тело В располагается в плоскости (рис. 2.20).

Точка М совершает сложное движение, состоящее из относительного (движение точки по желобу) и переносного (вращение точки вместе с пластиной вокруг оси АС) движений.

В

Рис. 2.20

ычислим абсолютную скорость точки :

.

Относительная скорость . Найдем положение точки М на пластине В через 1с. Для этого вычислим значение дуговой координаты при :

Если обозначить угол, на который опирается дуга ОМ, через  (рис. 2.20), то .

Относительное движение точки задано естественным способом. Приведем оси к точке М на траектории. Относительная скорость точки М при

Вектор относительной скорости лежит в соприкасающейся плоскости относительного движения – плоскость и направлена по касательной к траектории относительного движения – по оси (рис. 2.21, а).

а б

Рис. 2.21

Переносная скорость . В переносном движении точка движется в соприкасающейся плоскости переносного движения, параллельной плоскости , по окружности радиусом (рис. 2.21, б).

Задано уравнение вращения пластины В: , тогда

Переносное движение ускоренное, т. к. >0, >0, дуговые стрелки и направлены в одну сторону (рис. 2.21, б). Приведем оси к точке М.

Вычислим радиус кривизны траектории при переносном движении точки М в момент времени ( ):

=R − = R(1− cos) = 30(1 – cos( )) = 30(1 – 0,707) = 8,79 см.

Переносная скорость V_е

.

Вектор переносной скорости направлен по касательной к траектории в точке М – ось (рис. 2.21, б). Направление оси согласуется с направлением дуговой стрелки .

Так как в данном случае векторы взаимно перпендикулярны (вектор скорости расположен в плоскости , вектор скорости направлен по оси , т.е. ), то модуль абсолютной скорости точки М:

.

Вычислим абсолютное ускорение точки М. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и Кориолисова ускорений

.

Относительное ускорение . Относительное движение точки задано естественным способом – точка движется по окружности радиусом в соприкасающейся плоскости относительного движения . Приведем к точке оси естественного трехгранника (рис 2.22, а). Ось совпадает с направлением , ось перпендикулярна оси и направлена вовнутрь вогнутости траектории по радиусу .

Относительное ускорение равно

Здесь, при t = 1 с:

.

Точка движется с замедлением, поскольку векторы >0, <0, вектор и вектор имеют разное направление по оси . Векторы и направлены по осям и соответственно и лежат в плоскости .

а б

Рис. 2.22

Переносное ускорение . Движение точки в ее переносном движении криволинейное. Точка движется по окружности радиусом в соприкасающейся плоскости переносного движения, параллельной плоскости . Приведем к точке оси естественного трехгранника (рис 2.22, б). Ось совпадает с направлением , ось перпендикулярно оси и направлена вовнутрь вогнутости, т. е. по радиусу МК.

Переносное ускорение, рис. 2.22, б:

.

Здесь при t = 1 с:

Векторы и направлены по осям и соответственно.

а б

Рис. 2.23

Ускорение Кориолиса . Вектор ускорения Кориолиса

,

его модуль

.

Вектор направлен по оси вращения АС. Угол между векторами и равен (=135^о) (рис. 2.23, а).

Итак,

Направление вектора по правилу Журавского: поворачиваем на 90 по направлению дуговой стрелки вектор направлен параллельно оси (рис. 2.23, б).

Для вычисления модуля абсолютного ускорения используем способ проекций. Спроецируем все составляющие абсолютного ускорения на оси . Имеем (рис 2.22 и рис. 2.23, б):

	Модуль абсолютного ускорения (рис. 2.24): Направление вектора определим геометрически. Совместим с точкой декартову систему координат (рис. 2.24). Ответ: см/с; см/с2.
Рис. 2.24