Цилиндр

Определения

Цилиндром называется фигура, полученная при вращении прямоугольника вокруг прямой, содержащей его сторону (рис.153).

Прямая СD- ось цилиндра.

Рис. 153

Образующей цилиндра называется сторона AB прямоугольника ABCD, при вращении прямоугольника она образует боковую поверхность цилиндра.

Основания цилиндра – это круги, которые образуются от вращения сторон DA и BC прямоугольника ABCD

Полная поверхность цилиндра состоит из двух его оснований и боковой поверхности.

Высота цилиндра – отрезок перпендикуляра к основаниям цилиндра, заключенный между этими основаниями.

Осевое сечение цилиндра - прямоугольник( MNPQ)(рис. 154), полученный при

пересечении плоскости, проходящей через ось цилиндра

перпендикулярно его основаниям.

Рис. 154

Развертка боковой поверхности цилиндра - прямоугольник (рис.155 ), длина одной из сторон которого равна высоте цилиндра, а длина другой стороны – длине окружности основания цилиндра.

Рис.155

Контрольные вопросы

1.Вставьте пропущенное слово: Цилиндром называется фигура, полученная при вращении … вокруг прямой, содержащей его сторону

(прямоугольника)

2. Вставьте пропущенное слово: … цилиндра – отрезок перпендикуляра к основаниям цилиндра, заключенный между этими основаниями.

(Высота).

3. Вставьте пропущенное слово: …сечение цилиндра – прямоугольник, полученный при пересечении плоскости, проходящей через ось цилиндра

перпендикулярно его основаниям.

(Осевое)

4. Вставьте пропущенное слово: Развертка боковой поверхности цилиндра – … , длина одной из сторон которого равна высоте цилиндра, а длина другой стороны – длине окружности основания цилиндра.

(Прямоугольник)

5.Осевое сечение цилиндра – квадрат с площадью 25 см ². Вычислите

высоту цилиндра.

а) 5; б) 2,5; в) 4 ; г) 3.

6. Площадь осевого сечения цилиндра равна 30см². Площадь основания цилиндра 25π см² Вычислить высоту цилиндра.

а) 5; б) 4; в) 6 ; г)3.

г)

7.Площадь развертки боковой поверхности цилиндра равна 48π, радиус основания цилиндра равен 4 см. Найдите высоту цилиндра.

а) 5; б) 4; в) 6 ; г) 3.

в)

8.Радиус основания цилиндра равен 5см. Высота цилиндра равна 4см.

Площадь развертки боковой поверхности цилиндра равна ( в см ²):

а) 50 π; б) 40 π; в) 20 π; г) 3 0 π.

9. Осевое сечение цилиндра – квадрат с площадью 25 см ². Вычислите

радиус основания цилиндра.

а) 5; б) 2,5; в) 4 ; г) 3.

б)

10. Длина окружности основания цилиндра равна 40 π. Высота цилиндра равна

10. Площадь осевого сечения цилиндра равна

а) 400; б)200; в) 100 ; г) 300.

a)

11. Основание цилиндрической бочки радиусом 0,6м и высотой 1,6 м находится на полу помещения высотой 1,9 м .

Можно ли выкатить бочку из этого помещения?

(нет)

12.Площадь осевого сечения цилиндра равна 60. Высота цилиндра 10см.

Длина окружности основания равна:

а) 5π; б) 4π; в) 6π; г) 3 π.

13. Развертка цилиндра – прямоугольник с диагональю 16см и углом между

диагоналями 60º. Найдите длину окружности основания цилиндра.

а) ; б)8; в) ; г) 12.

a)

14. Развертка цилиндра – прямоугольник с диагональю 16см и углом между

диагоналями 60º. Найдите высоту цилиндра.

а) 6; б)8; в)9; г) 12.

15.Диагональ развертки боковой поверхности цилиндра равна 6см и образует с

основанием развертки угол 30º. Найдите длину окружности основания цилиндра.

а) ; б)8; в) ; г) .

г)

Сечения цилиндра плоскостью =4

1.Сечение, проходящее через две образующие цилиндра (рис.156), есть

прямоугольник (KFEL). Оно параллельно оси цилиндра.

Рис. 156

2. Сечение, параллельное основаниям цилиндра( рис.157), есть круг.

Рис. 157

3. Cечение, не параллельное основаниям цилиндра и не пересекающее его основания есть эллипс.

Рис. 158

Эллипс- это множество точек плоскости сумма расстояний от которых до двух заданных точек этой плоскости есть величина постоянная.

Покажем, что сечение, не параллельное основаниям цилиндра и не пересекающее его основания есть эллипс.

Пусть плоскость α пересекает поверхность цилиндра по некоторой линии L. Рассмотрим два шара, радиусы которых равны радиусам основания цилиндра, касающиеся поверхности цилиндра и плоскости (рис158). Точки касания c плоскостью обозначим F₁ и F₂. Линии пересечения поверхности цилиндра и шара обозначим L₁ и L₂. Выберем любую точку x линии пересечения L и проведем через нее образующую цилиндра. Обозначим длину этой образующей между точками пересечения A и B c линиями L₁ и L₂ 2a.

По теореме о касательных, проведенных из одной точки к сфере будем иметь:

xA = x F₁, xB = x F₂ . Cложим последние два равенства, получим

x F₁ + x F₂ = xA + xB = AB =2a. Таким образом, сумма расстояний от двух заданных точек F₁ и F₂ до произвольной точки линии L есть величина постоянная.

Значит, линия L – эллипс. Доказательство закончено.

Контрольные вопросы

1. Вставьте пропущенные слова: Сечение, проходящее через две образующие цилиндра, есть прямоугольник … .

(прямоугольник)

2. Вставьте пропущенные слова: Сечение, параллельное основаниям цилиндра есть… .

(круг)

3. Вставьте пропущенные слова: Сечение, не параллельное основаниям цилиндра и не пересекающее его основания есть … .

(эллипс)

4. Cечение цилиндра плоскостью, перпендикулярной оси цилиндра есть:

а) круг; б)эллипс; в) прямоугольник.

а)

5.Cечение цилиндра плоскостью, параллельной оси цилиндра есть:

а) круг; б)эллипс; в) прямоугольник.

б)

6. Cечение цилиндра плоскостью, образующей с его осью угол 30^° может быть

а) кругом; б)эллипсом; в) прямоугольником.

7. Радиус основания цилиндра равен 4см. Найдите длину линии пересечения цилиндрической поверхности с плоскостью, параллельной основанию цилиндра.

(8π см)

8. Радиус основания цилиндра равен 4см. Найдите площадь пересечения цилиндра с плоскостью, параллельной основанию цилиндра.

(16π см²)

9. Площадь сечения цилиндра, плоскостью параллельной его оси прямоугольник равна 240 см ² . Найдите радиус основания цилиндра, если сечение удалено от оси цилиндра на расстояние 9см, а высота цилиндра равна 10см.

(5см или 3√5см.)

10. Сечением цилиндра, параллельным его оси является прямоугольник со сторонами 12 и 8 см. Найдите радиус основания цилиндра, если сечение удалено от оси цилиндра на расстояние 3см.

(15см ).

11. Осевые сечения двух цилиндров равны. Тогда:

а) равны радиусы оснований цилиндров; б) равны высоты оснований цилиндров; в) высоты цилиндров прямо пропорциональных радиусам.

г) высоты цилиндров обратно пропорциональны их радиусам.

г)

9.Площадь осевого сечения цилиндра равна 30см². Площадь основания цилиндра 25πсм² . Вычислить площадь сечения, параллельного оси и отстоящего от нее на 4см.

(18см²)

12. Cечение цилиндра плоскостью, пересекающей все образующие цилиндра может быть

а) круг; б)эллипс; в) прямоугольник.

а),б ).

13. Сечение цилиндра, плоскостью параллельной его оси - квадрат. Радиус основания цилиндра 5 см, высота цилиндра равна 6см. Найдите расстояние от этого сечения до оси цилиндра.

(4)

14.Как расположены точки на поверхности цилиндра, равноудаленные от двух точек его основания?

а) на окружности; б) на эллипсе; в) на двух сторонах прямоугольника – образующих цилиндра.

в)

15. Если расстояние между двумя точками сечения цилиндра равно 8см, то радиус основания цилиндра и высота могут быть равными:

а) 3 и 4; б) 3 и 6; в) 5 и 8; г) 1 и 7.

б), в).

Прямой круговой конус = 5

Определение

Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг прямой, содержащей его катет (рис. 159).

Прямая СA- ось конуса.

Вершина конуса - это вершина A треугольника ABC.

Образующей конуса называется гипотенуза (сторона AB ) прямоугольного треугольника ABC, при вращении прямоугольного треугольника она образует боковую поверхность конуса.

Основания конуса – это круг, который образуется от вращения

стороны BC прямоугольного треугольника ABC.

Полная поверхность конуса состоит из его основания и боковой

поверхности.

Высота конуса – отрезок перпендикуляра из вершины конуса к плоскости

основания.

Рис. 159

Осевое сечение конуса- треугольник (MNP), полученный при

пересечении плоскости, проходящей через ось конуса

перпендикулярно его основанию( рис. 160).

Рис. 160

Развертка боковой поверхности конуса – есть круговой сектор

(рис. 161), радиус которого равен образующей конуса, а длина

дуги сектора – длине окружности основания конуса:

L=ОA, =2πR, .

Рис. 161

Контрольные вопросы

1.Вставьте пропущенное слова: Конусом называется фигура, полученная при вращении … вокруг прямой, содержащей его катет.

(прямоугольного треугольника)

2. Вставьте пропущенное слово: … конуса – отрезок из вершины вершины конуса к плоскости основания.

(Высота).

3. Вставьте пропущенное слово: … сечение конуса треугольник, полученный при пересечении плоскости, проходящей через ось конуса перпендикулярно его основанию.

(Осевое)

4. Вставьте пропущенные слова: Развертка боковой поверхности конуса – есть круговой … радиус которого равен образующей конуса, а длина дуги сектора – длине окружности основания конуса.

(сектор)

5.Радиус основания конуса равен 3см, высота конуса 4 см. Найдите образующую конуса.

а) 7; б) 6; в) 5.

в)

6.Осевое сечение конуса – это

а) прямоугольный неравнобедренный треугольник б) произвольный треугольник ; в) равнобедренный треугольник .

Выберите правильный ответ.

в)

7. Осевое сечение – правильный треугольник со стороной 10 см.

Длина окружности основания конуса равна

а) 10π; б) 20π; в) 5π.

б)

8. Осевое сечение усеченного конуса – это

а) прямоугольная трапеция; б) равнобедренная трапеция; в) равнобедренный треугольник .

Выберите правильный ответ.

б)

9. Радиус основания конуса равен 5см. Осевое сечение – прямоугольный треугольник. Его площадь равна:

а) 50; б)25; в) 20; г) 12,5.

б)

10. Образующая конуса равна 8 см, угол при вершине осевого сечения равен 30°.

Площадь осевого сечения этого конуса:

а)32; б)16; в) 64; г) 12.

б)

11. Образующая конуса равна 10 см, диаметр основания равен 16см. Высота конуса равна

а)6; б)8; в) 4; г) 12.

а)

12. Площадь основания конуса 16π. Образующая равна 5 см. Площадь осевого сечения конуса равна:

а)6; б)8; в) 4; г) 12.

г)

13.Если угол между образующей и высотой конуса равен 30°, то центральный угол в развертке конуса равен

а)30°; б) 30°; в) 180°;г) 120° .

в)

14.Радиус сектора равен 3 м, его угол равен 120°. Сектор свернут в коническую поверхность. Найдите радиус основания конуса.

г) 1м

15. Радиус основания конуса равен 3 см. Высота конуса 4 см.

Найдите центральный угол в развертке боковой поверхности конуса.

а) 216°; б) 120°; в) 180°; г) 128° .

Сечения конуса плоскостью = 6

1.Осевое сечение конуса - треугольник ( рис.160), полученный при пересечении плоскости, проходящей через ось конуса перпендикулярно его основанию.

Рис. 160

2. Сечение, проходящее через две образующие конуса (рис.162), есть равнобедренный треугольник.

Рис. 162

3. Сечение, параллельное только одной образующей конуса ( рис.163 ), есть парабола .

Рис. 163

4. Сечение, параллельное двум образующим конуса ( рис.164 ), есть гипербола.

Рис. 164

5. Сечение, не параллельное основанию и пересекающее все образующие конуса ( рис.165 ), есть эллипс.

Рис. 165

Контрольные вопросы

1. В конусе проведено сечение, параллельное основанию конуса, которое делит высоту в отношении 1: 2, считая от вершины. Каков радиус сечения, если радиус основания равен 6см?

(2)

2. В конусе проведено сечение, параллельное основанию конуса, которое делит высоту в отношении 1: 2, считая от вершины. Какова длина линии пересечения плоскости с поверхностью конуса, если радиус основания равен 12см?

(8π см)

3. В конусе проведено сечение, параллельное основанию конуса, которое делит высоту в отношении 1: 2, считая от вершины. Какова площадь сечения если радиус основания равен 9 см?

(9π см ²)

4. Сечение, проходящее через вершину конуса и стягивает дугу в 60°, если образующая конуса равна 5, а высота основания – 3 см, то хорда этой дуги равна

а)6; б)8; в) 4; г) 12.

в)

5. Высота конуса равна 4см. Угол между высотой и образующей равен 60°.

Площадь сечения, проведенного через две взаимно перпендикулярные образующие конуса равна (в cм ²)

а)36; б)18; в) 24; г) 32.

г)

6. В равностороннем конусе радиус основания равен 2см.Площадь сечения, проведенного через две образующие конуса, образующие между собой 30 ^° равна (в cм ²)

а)6; б)18; в) 4; г) 12.

в)

1. Как расположены на поверхности конуса точки, равноудаленные от двух точек окружности основания?

а) на окружности; б)на двух образующих конуса; в) на параболе ;

г)на гиперболе.

б)

2. Угол в осевом сечении конуса равен 65°. Может ли угол в сечении, проходящем через вершину конуса, быть равным:

а) 26°; б) 20°; в) 80°; г) 128° ?

а),б) – может.

3. Угол в осевом сечении конуса равен 105°. Может ли угол в сечении, проходящем через вершину конуса, быть равным:

а) 60°; б) 120°; в) 80°; г) 100° ?

а),в), г) – может.

4. Угол в осевом сечении конуса равен 120°. Может ли угол в сечении, проходящем через вершину конуса, быть равным:

а)160°; б) 30°; в) 90°; г) 100° ?

б),в), г) – может

11.

Площадь осевого сечения конуса равна 25πсм² .Площадь основания

конуса 25πсм². Вычислите площадь сечения, которое проходит через две

образующие конуса и пересекает основание конуса по хорде длина

которой 6см.

12.

Высота конуса 20см, радиус его основания 25см. Найдите площадь сечения, проведенного через вершину, если его расстояние от центра основания конуса равно 12.

( 5см²)

13. Площадь осевого сечения конуса равна 25см² . Может ли площадь сечения, проходящего через вершину конуса быть равной

а) 12см²; б) 20см²; в) 5см²; г) 125см²?

а) - г) может.

14. Площадь сечения конуса, проходящего через вершину конуса равна 100см² . Может ли площадь осевого сечения быть равной

а) 40см²; б) 50см²; в) 60см²; г) 125см²?

а) - г) может.

15. Может ли площадь сечения, проходящего через вершину конуса быть в 1000 раз больше площади осевого сечения?

(Может)

Усеченный конус =7

Определение

Усеченным конусом называется часть конуса, заключенная между основанием и плоскостью, параллельной основанию( рис.166).

AA₁- образующая, OO₁- высота, круги с центрами O и O₁, радиусами R и r - основания .

Рис. 166

Осевое сечение усеченного конуса – равнобедренная трапеция, полученная при

пересечении плоскости, проходящей через ось усеченного конуса

перпендикулярно его основанию( рис.167).

Рис. 167

Развертка боковой поверхности усеченного конуса- часть кругового кольца.

Чтобы получить развертку боковой поверхности усеченного конуса, дополним

его до полного конуса и сделаем развертку полного конуса, а затем рассмотрим

на этой развертке развертку конуса с тем же центральным углом и меньшим радиусом, получим часть кольца( рис.168).

Рис. 168

Контрольные вопросы

1.Вставьте пропущенные слова: … … называется часть конуса, заключенная между основанием и плоскостью, параллельной основанию конуса.

(Усеченным конусом)

2. Осевое сечение усеченного конуса – это

а) прямоугольная трапеция; б) равнобедренная трапеция; в) равнобедренный треугольник .

Выберите правильный ответ.

б)

3. Развертка боковой поверхности усеченного конуса это

а) сектор; б) равнобедренная трапеция; в) равнобедренный треугольник; г) часть кольца.

Выберите правильный ответ.

г)

4.Радиусы основания усеченного конуса равны 4 и 1 см, образующая 5см. Найдите его высоту.

(4)

5.Радиусы основания усеченного конуса равны 5 и 11см.Высота конуса – 8см.

Найдите его площадь его осевого сечения.

(64 см ²)

6. Радиусы основания усеченного конуса равны 5 и 11см.Высота конуса – 8см.

Найдите его образующую.

(10)

7. Радиусы основания усеченного конуса равны 5 и 11см. Образующая составляет с плоскостью основания угол 45°. Найдите площадь осевого сечения конуса.

(48 см ²)

8. Радиусы основания усеченного конуса равны 5 и 11см. Образующая составляет с плоскостью основания угол 60°. Найдите образующую конуса.

(12см )

9.Усеченный конус может быть получен вращением

а) треугольника вокруг одной из его высот; б) прямоугольной трапеции вокруг меньшей боковой стороны.

Выберите правильный ответ.

б)

10. Прямоугольная трапеция вращается вокруг меньшей боковой стороны.

Найдите образующую фигуры вращения, если стороны оснований трапеции относятся как 1:2, а высота равна 6 см и равна меньшей боковой стороне.

( см)

11. Осевое сечение усеченного конуса – трапеция с высотой 4 см и основаниями 10 и 16 см. Найдите образующую усеченного конуса.

( 5)

12.Осевое сечение усеченного конуса – трапеция с боковой стороной 10 см и основаниями 20 и 32 см.Найдите высоту усеченного конуса.

( 8)

13.Высота усеченного конуса равна 6 см. Радиусы оснований относятся как 1:2.

Угол между образующей и плоскостью оснований 45°.

Найдите площадь осевого сечения конуса.

((54 см ²)

14. Радиусы основания усеченного конуса равны 5 и 10см. Через две его образующие проведено сечение, отсекающее от окружности оснований дуги 90° и образующее с плоскостью оснований угол 60°.Найдите площадь сечения.

(75см ²)

15. Радиусы оснований усеченного конуса равны 5см и 2см. Высота конуса 4 см.

Найдите центральный угол в развертке боковой поверхности конуса.

а) 216°; б) 120°; в) 180°; г) 128° .

а)

Сфера и шар. Элементы сферы и шара=8

Определения

1.Сферой называется множество всех точек пространства, находящихся на положительном расстоянии R от данной точки.

2.Центр сферы – данная точка O (рис.169), отрезок OM –радиус сферы.

Любой отрезок, соединяющий центр сферы с точкой сферы называется радиусом сферы.

Рис. 168

3.Шаром называется множество всех точек пространства, находящихся на расстоянии, не больше положительного R от данной точки или

шар – это часть пространства, ограниченная сферой.

Радиус шара – это радиус ограничивающей его сферы.

Шар можно получить при вращении полукруга вокруг оси, которая содержит диаметр полукруга.

Отрезок, соединяющий две точки сферы, называется хордой сферы.

Хорда, проходящая через центр сферы называется диаметром сферы.

Контрольные вопросы

1.Вставьте пропущенное слово: … называется множество всех точек пространства, находящихся на положительном расстоянии R от данной точки.

(сферой)

2.Вставьте пропущенное слово: … называется множество всех точек пространства, находящихся на расстоянии, не больше положительного R от данной точки.

(Шаром)

3. Вставьте пропущенное слово: Любой отрезок, соединяющий центр сферы с точкой сферы называется … сферы.

(Радиусом)

4. Вставьте пропущенное слово: …можно получить при вращении полукруга вокруг оси, которая содержит диаметр полукруга.

( шар)

5.Вставьте пропущенное слово: Отрезок, соединяющий две точки сферы, называется …сферы.

(хордой)

6. Вставьте пропущенное слово: Хорда, проходящая через центр сферы называется …сферы.

(диаметром)

7. Установите соответствие

а) Множество всех точек пространства, находящихся на положительном расстоянии R от данной точки;

б) ) Множество всех точек плоскости, находящихся на положительном расстоянии R от данной точки;

в) Множество всех точек пространства, находящихся на расстоянии, не больше положительного R от данной точки.

г) Множество всех точек плоскости, находящихся на расстоянии, не больше положительного R от данной точки.

а) круг; б) шар; в) сфера; г) окружность.

( а) – в), б)- г), в) – б) г) – а).

8. Составьте из частей определение сферы: а)находящихся на положительном расстоянии R , б) множество всех точек, в) от данной точки, г) пространства.

б), г), а),в).

9. Составьте из частей определение шара : а)находящихся на расстоянии, б) множество всех точек, в) от данной точки, г) пространства д) не больше положительного R.

б), г), а), д),в).

10. Вставьте попущенное слово: Центр шара лежит на прямой, … любому его круговому сечению.

(перпендикулярной)

11. Вставьте попущенное слово: Центр шара лежит на прямой, проходящей через центры двух его …круговых сечений.

(параллельных)

12.На сколько частей разбивают сферу две окружности, расположенные на ней

а) 2,б) 3,в)4 , г)5. ?

б)

13. Сколько различных сфер можно провести через две точки?

а) 2,б) 3, в) 1 , г) бесконечно много.

г)

14. Сколько различных сфер можно провести через три точки, не лежащие на одной прямой?

а) 1 ,б) 3, в) 4 , г) бесконечно много.

г)

15. Сколько различных сфер можно провести через четыре точки, не лежащие на

в одной плоскости?

а) 1 ,б) 3, в) 4 , г) бесконечно много.

a)

Уравнение сферы = 9

Пусть задана прямоугольная система координат ( рис. 169). Составим уравнение сферы с центром в точке S(a; b; c) и радиусом R.

Рис. 169

Для каждой точки M ( x;y;z), принадлежащей сфере и только для таких точек, выполняется равенство:

SM = R.

Пользуясь формулой расстояния между двумя точками, получим

(x-a) ² +( y- b ) ² + (z - c ) ² = R ² (1) .

Уравнение (1) и есть уравнение сферы с центром в точке (a; b; c) и радиусом R.

Если a=b=c=0, то получим уравнение сферы с центром в начале координат

x-² +y ² + z ² = R ² .

Контрольные вопросы

1. Сфера задана уравнением: (x- 4) ² +( y - 4 ) ² + (z - 5 ) ² = 16.

Определите координаты центра сферы.

( 4; 4; 5).

2. Сфера задана уравнением: (x- 4) ² +( y - 4 ) ² + (z - 5 ) ² = 16.

Определите радиус сферы.

( 4)

3. Сфера задана уравнением: x ² + y ² + (z + 1 ) ² = 1.

Определите координаты центра сферы.

( 0; 0; -1).

4.Составьте уравнение сферы с центром в точке S(2; -5; -1) и радиусом 3.

((x- 2) ² +( y +5 ) ² + (z +1 ) ² = 9)

5. Составьте уравнение сферы с центром в начале координат и радиусом 1.

(x ² +y + ² + z ² = 1)

6. Принадлежит ли точка (4; -1; 0) сфере (x- 4) ² +( y +1 ) ² + (z - 5 ) ² =25

( принадлежит)

7. Принадлежит ли точка (2 ; 1; 3) сфере (x - 2 ) ² +( y + 1 ) ² + (z - 5 ) ² =16

(не принадлежит)

8. Найдите координаты точки пересечения сферы

(x - 2 ) ² +( y + 1 ) ² + (z - 5 ) ² =16

с осью абсцисс.

(6; 0;0), (-2 ; 0;0).

9. Найдите координаты точечки пересечения сферы

(x - 2 ) ² +( y + 1 ) ² + (z - 5 ) ² =16

с осью ординат

(0; 3;0), (0; -4 ;0).

10. Найдите координаты точечки пересечения сферы

(x - 2 ) ² +( y + 1 ) ² + (z - 5 ) ² =16

с осью аппликат

(0; ;1), (0; 0 ;9).

11. Найдите наименьшее расстояние от точки ( 3; -2 ;6 ) до сферы

x ² + y ² + z ² = 1.

(6)

12. Найдите наименьшее расстояние от точки ( 4; -3 ;0 ) до сферы

x ² + y ² + z ² = 1.

(4)

13.Составьте уравнение плоскости, касающейся сферы x ² + y ² + z ² = 9.

в точке (0; 3; 0)

(y - 3 = 0)

14. Составьте уравнение плоскости, касающейся сферы x ² + y ² + z ² = 9.

в точке (2; -2;-1)

( 2x- 2y – z- 9 = 0)

15. Составьте уравнение сферы радиуса 5 см, касающейся всех координатных плоскостей, если все координаты центра положительны

((x - 5 ) ² +( y - 5) ² + (z - 5 ) ² = 5)

Сечение шара плоскостью = 10

Рассмотрим сферу с центром в точке O и плоскость α ( рис.170 )

Проведем ОС α. Пусть OC = d.

Если d > r, то сфера и плоскость общих точек не имеют.

Если d < r, то сфера и плоскость имеют общие точки.

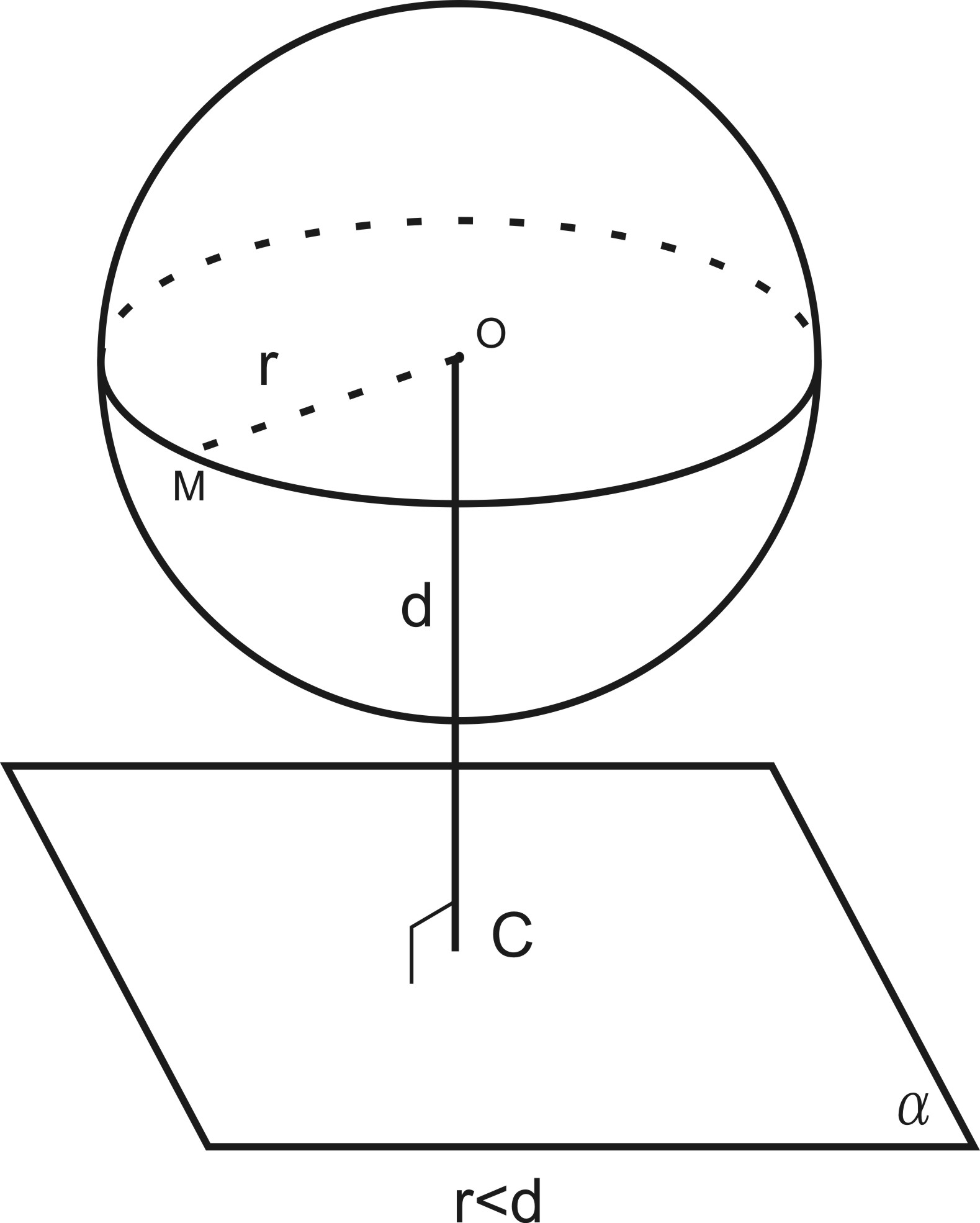Рис. 170

Теорема

Сечение сферы плоскостью – окружность.

Доказательство

Пусть M – любая точка пересечения сферы с плоскостью α ( рис.170). Соединим ее с точкой С и проведем радиус OM. По определению перпендикуляра к плоскости ОС СM.

По теореме Пифагора CM = , где OC = d, r – радиус сферы.

Величины r и d – постоянные, следовательно, для любой точки пересечения сферы и плоскости расстояние до точки C есть величина постоянная, следовательно, по определению окружности – эта линия есть окружность.

Доказательство закончено.

Следствие 1

Сечение шара плоскостью есть круг.

Следствие 2

Сечения шара плоскостью, равноудаленные от центра, равны

Следствие 3

Сечения шара плоскостью тем больше, чем ближе оно расположено к центру.

Определение1

Сечения шара плоскостью, проходящей через центр шара, называется большим кругом, а его окружность – окружностью большого круга.

Определение2

Точки пересечения сферы с диаметром, перпендикулярным большому кругу, называются полюсами сферы.

Следствие 4

Два больших круга пересекаются по диаметру.

Следствие 5

Сечением шара плоскостью является точка, если расстояние от центра шара до плоскости равно радиусу шара.

Контрольные вопросы

1. Вставьте пропущенные слова: Сечения шара плоскостью, проходящей через центр шара, называется … … .

(большим кругом)

2. Вставьте пропущенное слово: Сечения шара плоскостью тем больше, чем … оно расположено к центру.

(ближе)

3. Вставьте пропущенные слова: Сечения шара плоскостью, равноудаленные от центра, … .

(равны)

4. Радиус сферы равен 5 см, расстояние от центра сферы до плоскости α равно 6 см, тогда:

а) сфера и плоскость пересекаются; б) сфера и плоскость не имеют общих точек.

б)

5. Радиус сферы равен 5см, сфера и плоскость пересекаются, тогда расстояние от центра сферы до плоскости может быть равным (в см) :

а)6; б)8; в) 4; г) 1.

в), г).

6. Радиус сферы равен 5, сфера и плоскость не пересекаются, тогда расстояние от центра сферы до плоскости может быть равным (в см):

а)6; б) 2; в) 8; г) 3.

в), а).

7. Расстояние от центра сферы до плоскости равно 4 см, сфера и плоскость не пересекаются, тогда радиус сферы может быть равным (в см):

а) 6; б) 2; в) 8; г) 3.

б), г).

8. Шар радиуса 41см пересечен плоскостью на расстоянии 9 см от центра, тогда длина окружности сечения равна ( в см)

а) 20π; б) 80π; в) 5π.

б)

9. Шар пересечен плоскостью на расстоянии 8 см от центра, радиус сечения равен 15см, тогда радиус шара равен ( в см):

а)17; б) 23; в)12.

а)

10. Шар радиуса 41см пересечен плоскостью на расстоянии 9 см от центра, тогда площадь сечения равна в см ²:

а) 200π; б) 1600π; в) 80π.

б)

11.Как изменится площадь большого круга шара, если его радиус увеличить в два раза:

а) уменьшится в два раза; б) увеличится в два раза; в) увеличится в четыре раза; г) уменьшится в четыре раза?.

в)

12. Как изменится длина окружности большого круга шара, если его радиус увеличить в два раза:

а) уменьшится в два раза; б) увеличится в два раза; в) увеличится в четыре раза; г) уменьшится в четыре раза?

б)

13.На поверхности шара даны две различные точки. Сколько можно провести через них сечений шара плоскостью?

а) два; б) одно ; в)бесконечно много; г) нельзя установить.

в)

14. На поверхности шара даны две различные точки. Сколько можно провести через них больших кругов?

а) два; б) один ; в)бесконечно много; г) нельзя установить.

б)

15.Через какие две точки сферы можно провести только один большой круг?

а)любые ; б) концы одного диаметра шара; в) никакие; г) нельзя установить.

а)

Плоскость, касательная к сфере= 11

Определение

Касательной плоскостью к сфере называется плоскость, имеющая со сферой единственную общую точку( рис.171).

Рис. 171

Теорема1

Касательная плоскость перпендикулярна радиусу в конце его, лежащем на сфере.

Доказательство

Расcмотрим касательную плоскость α к сфере c c центром O радиуса r в точке M.

Покажем, что ОM α. Предположим, что плоскость не перпендикулярна радиусу сферы ( рис.172). Тогда проведем ОK α. Поскольку точка M – единственная общая точка сферы и плоскости, то точка K лежит вне сферы, а значит, расстояние OK больше радиуса сферы, т.е. OK > r или OK > OM. Но по предположению, OK – перпендикуляр, а OM – наклонная, проведенные из одной точки. Получили противоречие. Следовательно, наше предположение неверно, остается ОM α.

Доказательство закончено.

Рис. 172

Теорема2

Если плоскость перпендикулярна радиусу в конце его, лежащем на сфере,

то эта плоскость - касательная плоскость к сфере.

Доказательство

Расcмотрим к плоскость α и сферу c c центром O радиуса r .

Пусть ОM α. Покажем, что точка M – единственая общая точка сферы и плоскости. Предположим, что плоскость и сфера ( рис.172). имеют еще одну общую точку K. Тогда проведем ОK = r. Поскольку из одной точки можно провести только один перпендикулят к плоскости, то ОK - наклонная . Получили противоречие: перпендикуляр и наклонные проведенные из одной точки, равны. Следовательно, наше предположение неверно, остается M – единственная общая точка сферы и плоскости.

Доказательство закончено.

Контрольные вопросы.

1. Вставьте пропущенные слова: …к сфере называется плоскость, имеющая со сферой единственную общую точку

(Касательной плоскостью)

2. Вставьте пропущенное слово: Касательная плоскость …радиусу в конце его, лежащем на сфере.

(перпендикулярна

3.Вставьте пропущенные слова: Если плоскость перпендикулярна радиусу в конце его, лежащем на сфере, то эта плоскость - … …к сфере.

(касательная плоскость)

4. Радиус сферы равен 5 см , расстояние от центра сферы до плоскости α равно 5 см, тогда:

а) сфера и плоскость пересекаются; б) сфера и плоскость не имеют общих точек.

в) сфера и плоскость касаются.

в)

5. Радиус сферы равен 5см сфера и плоскость касаются , тогда расстояние от центра сферы до плоскости может быть равным (в см) :

а)5; б) 2; в)6.

а)

6.Сколько касательных плоскостей можно провести к сфере через точку, взятую на сфере:

а)1; б) 2; в) бесконечно много.

а)

7. Сколько касательных плоскостей можно провести к сфере через точку, взятую вне сферы:

а)1; б) 2; в) бесконечно много ?

в)

8. Сколько касательных прямых можно провести к сфере через точку, взятую на сфере:

а)1; б) 2; в) бесконечно много?

в)

9. Сколько касательных прямых можно провести к сфере через точку, взятую вне сфере:

а)1; б) 2; в) бесконечно много?

в)

10. Найдите множество всех точек пространства, которые являются центрами всех сфер, которые касаются данной плоскости в данной точке.

а) сфера; б) прямая, перпендикулярная данной плоскости, проходящая через данную точку ; в)плоскость, перпендикулярная данной плоскости, проходящая через данную точку

б)

11. Найдите множество всех точек пространства, которые являются центрами всех сфер, которые имеют данный радиус и касаются данной плоскости.

а) сфера; б) прямая, перпендикулярная данной плоскости, проходящая через данную точку ; в)плоскости, параллельные данной плоскости, находящиеся от нее на расстоянии, равным радиусу.

в)

12. Плоскость, касательная к сфере образует с сечением шара, проходящем

через точку касания угол 60º. Найдите длину окружности сечения, если

радиус шара равен 6 см.

( )

13. Сфера касается граней двугранного угла, величина которого равна 60º.

Найдите радиус сферы, если расстояние от ее центра до граней

двугранного угла равно 26см.

(13см)

14.Радиус сферы равен 63 см. Точка касательной плоскости находится на расстоянии 16 см от точки касания. Найдите ее наименьшее расстояние от сферы.

(2)

15. Радиус сферы равен 63 см. Точка касательной плоскости находится на расстоянии 16 см от точки касания. Найдите ее наибольшее расстояние от сферы.

(128)

угольный треуг