Плоскость, касательная к сфере
Определение
Касательной
плоскостью к сфере называется
плоскость, имеющая со сферой единственную
общую точку)
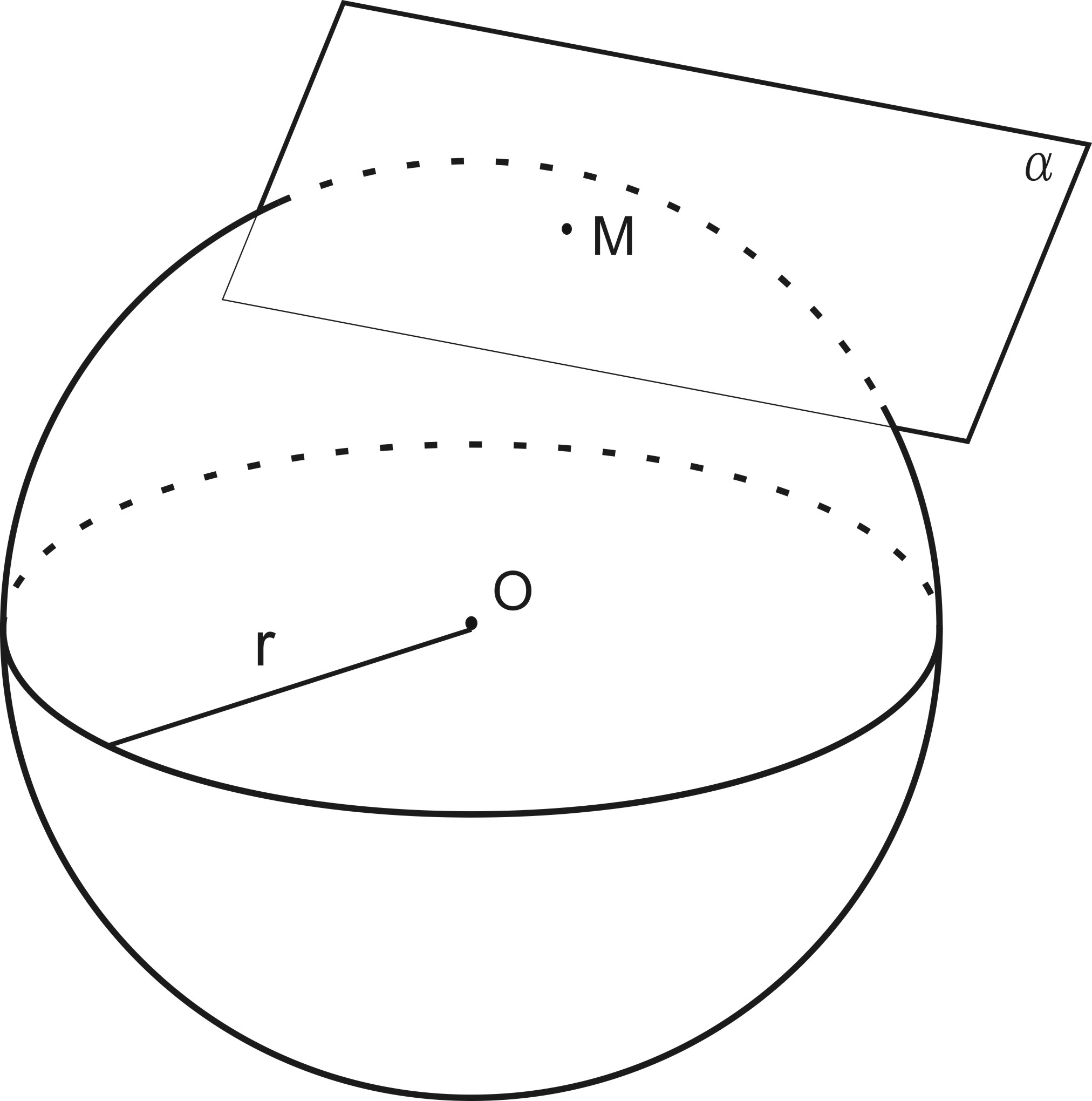
Теорема1
Касательная плоскость перпендикулярна радиусу в конце его, лежащем на сфере.
Доказательство
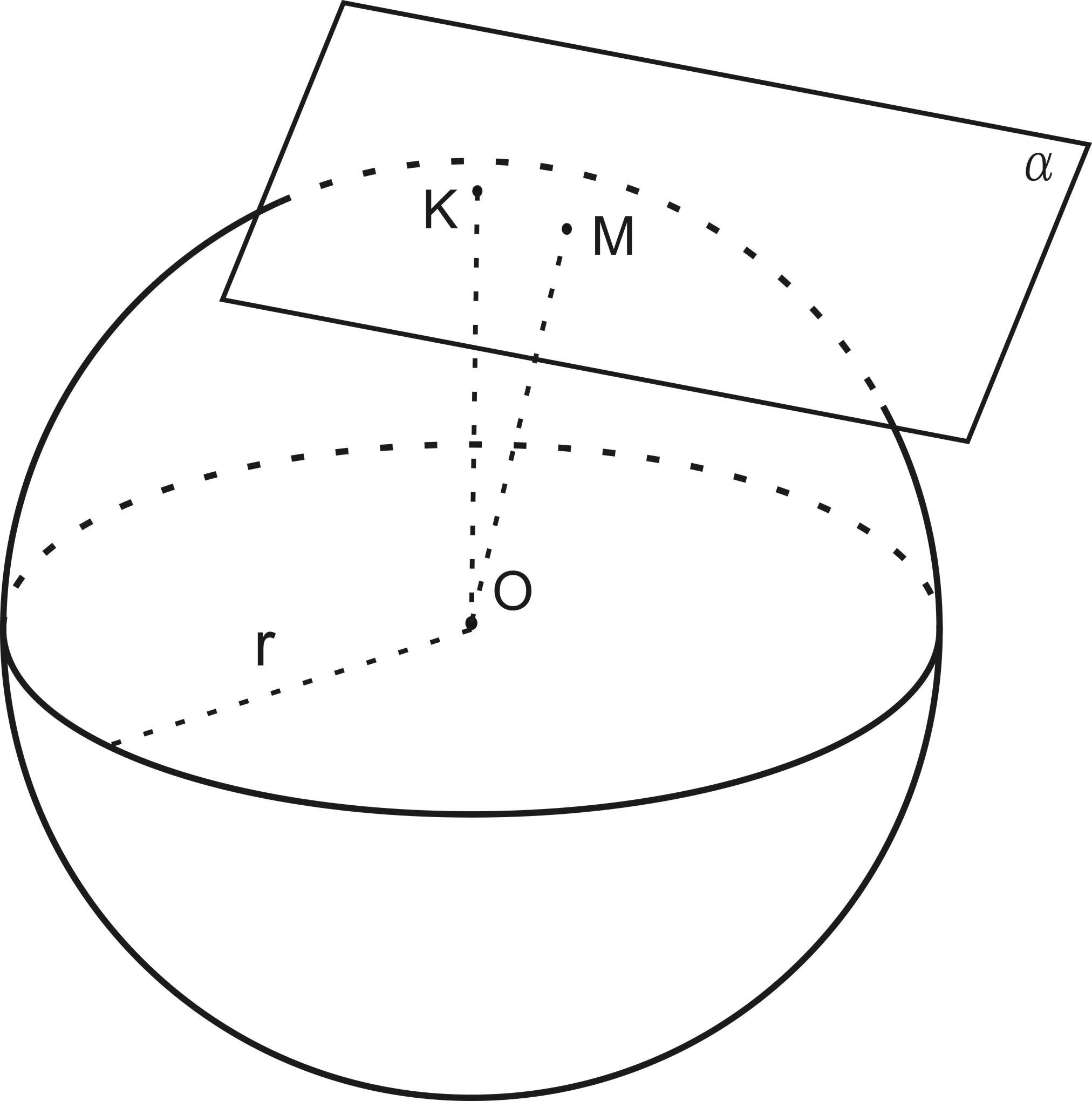
Расcмотрим касательную плоскость α к сфере c c центром O радиуса r в точке M.
Покажем, что ОM α. Предположим, что плоскость не перпендикулярна радиусу сферы ( рис.172). Тогда проведем ОK α. Поскольку точка M – единственная общая точка сферы и плоскости, то точка K лежит вне сферы, а значит, расстояние OK больше радиуса сферы, т.е. OK > r или OK > OM. Но по предположению, OK – перпендикуляр, а OM – наклонная, проведенные из одной точки. Получили противоречие. Следовательно, наше предположение неверно, остается ОM α.
Доказательство закончено.
Теорема 2
Если плоскость перпендикулярна радиусу в конце его, лежащем на сфере,
то эта плоскость - касательная плоскость к сфере.
Доказательство
Расcмотрим к плоскость α и сферу c c центром O радиуса r .
Пусть ОM α. Покажем, что точка M – единственая общая точка сферы и плоскости. Предположим, что плоскость и сфера имеют еще одну общую точку K. Тогда проведем ОK = r. Поскольку из одной точки можно провести только один перпендикуляр к плоскости, то ОK - наклонная. Получили противоречие: перпендикуляр и наклонные проведенные из одной точки, равны. Следовательно, наше предположение неверно, остается M – единственная общая точка сферы и плоскости.
Доказательство закончено.
Тела вращения
Понятие тел вращения =1
Пусть дана прямая l, точка M, не принадлежащая прямой l . Через точку M проведем плоскость, перпендикулярную прямой l. В этой плоскости рассмотрим окружность с центром в точке O - пересечения прямой и плоскости и радиусом OM.
Говорят, что эта окружность получена при вращении точки M вокруг оси l,
т.е. окружность – фигура вращения точки вокруг оси ( рис.146 ).
Если в плоскости прямой l рассматривается некоторая фигура F, то фигура вращения рассматривается как фигура, полученная при вращении множества точек фигуры F ( рис.147 ).
Рис. 147
При вращении отрезка, перпендикулярного оси вращения может получиться
а) круг ( рис. 148); б) кольцо( рис.149);
Рис. 148 Рис. 149
При вращении отрезка, параллельного оси вращения получится цилиндрическая поверхность( рис.150);
Рис. 150
При вращении отрезка не параллельного и не перпендикулярного оси вращения получится
а) коническая поверхность ( рис.151) ; б) поверхность усеченного конуса
( рис.152);
Рис. 151 Рис. 152
Контрольные вопросы
1. При вращении отрезка, перпендикулярного оси вращения и пересекающего ось получится:
а) круг; б) окружность.
б)
2. При вращении отрезка, лежащего на прямой, перпендикулярной и оси вращения и не пересекающего ось, получится:
а) кольцо ; б) окружность; в) круг.
а)