Тела вращения

Понятие тел вращения 1

1. Пусть дана прямая l, точка M, не принадлежащая прямой l . Через точку M проведем плоскость, перпендикулярную прямой l. В этой плоскости рассмотрим окружность с центром в точке O - пересечения прямой и плоскости и радиусом OM.

Говорят, что эта окружность получена при вращении точки M вокруг оси l,

т.е. окружность – фигура вращения точки вокруг оси.

2. Если в плоскости прямой l рассматривается некоторая фигура F, то фигура вращения рассматривается как фигура, полученная при вращении множества точек фигуры F).

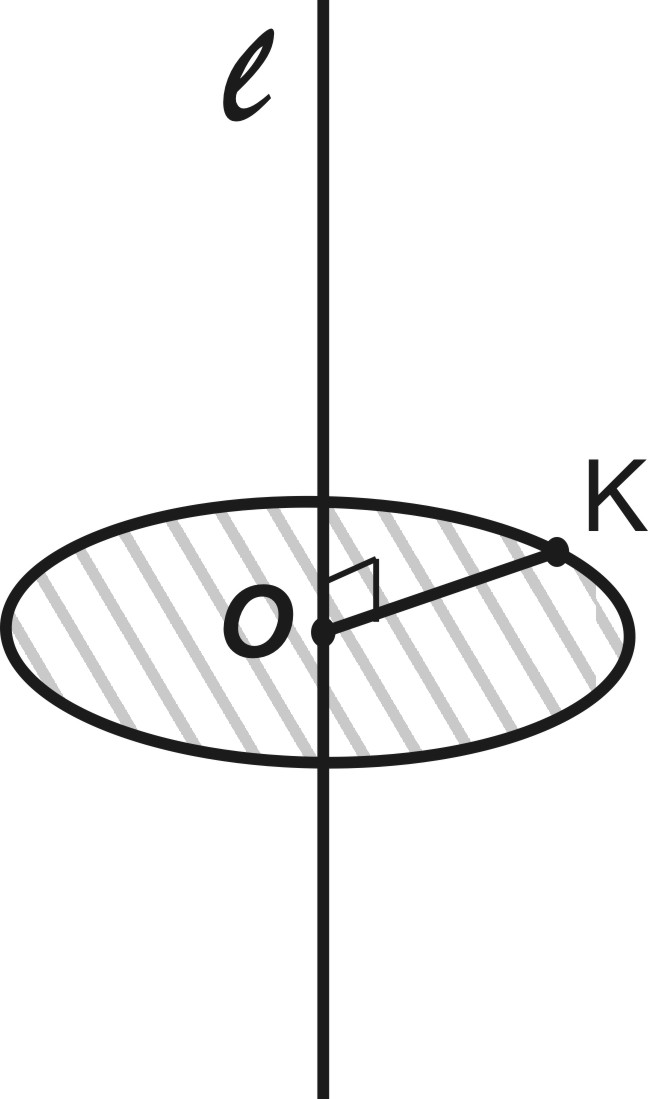
3. При вращении отрезка, перпендикулярного оси вращения может получиться:

а) круг);

б) кольцо.

4. При вращении отрезка, параллельного оси вращения получится

цилиндрическая поверхность.

5. При вращении отрезка не параллельного и не перпендикулярного оси вращения получится

а) коническая поверхность

б) поверхность усеченного конуса

Цилиндр

Определения

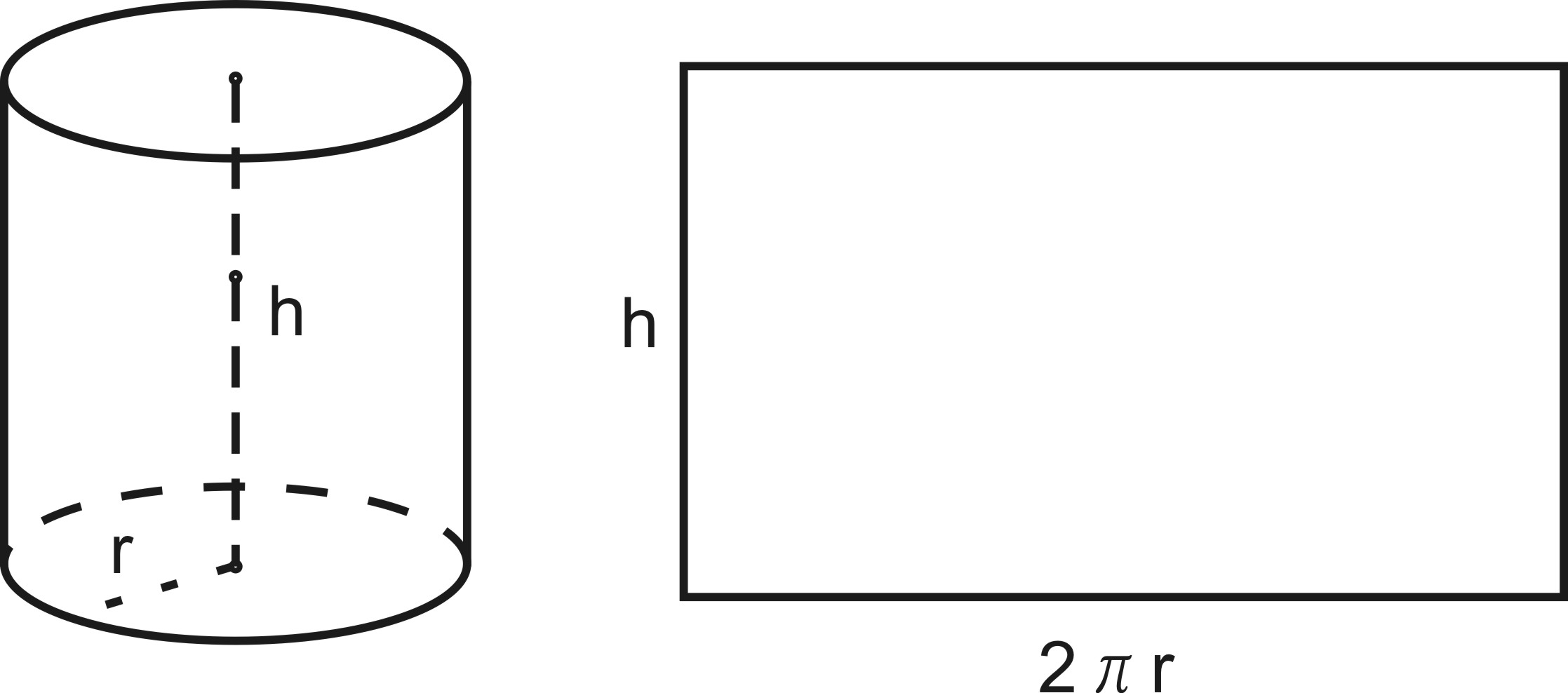
Цилиндром называется фигура, полученная при вращении прямоугольника

вокруг прямой, содержащей его сторону.

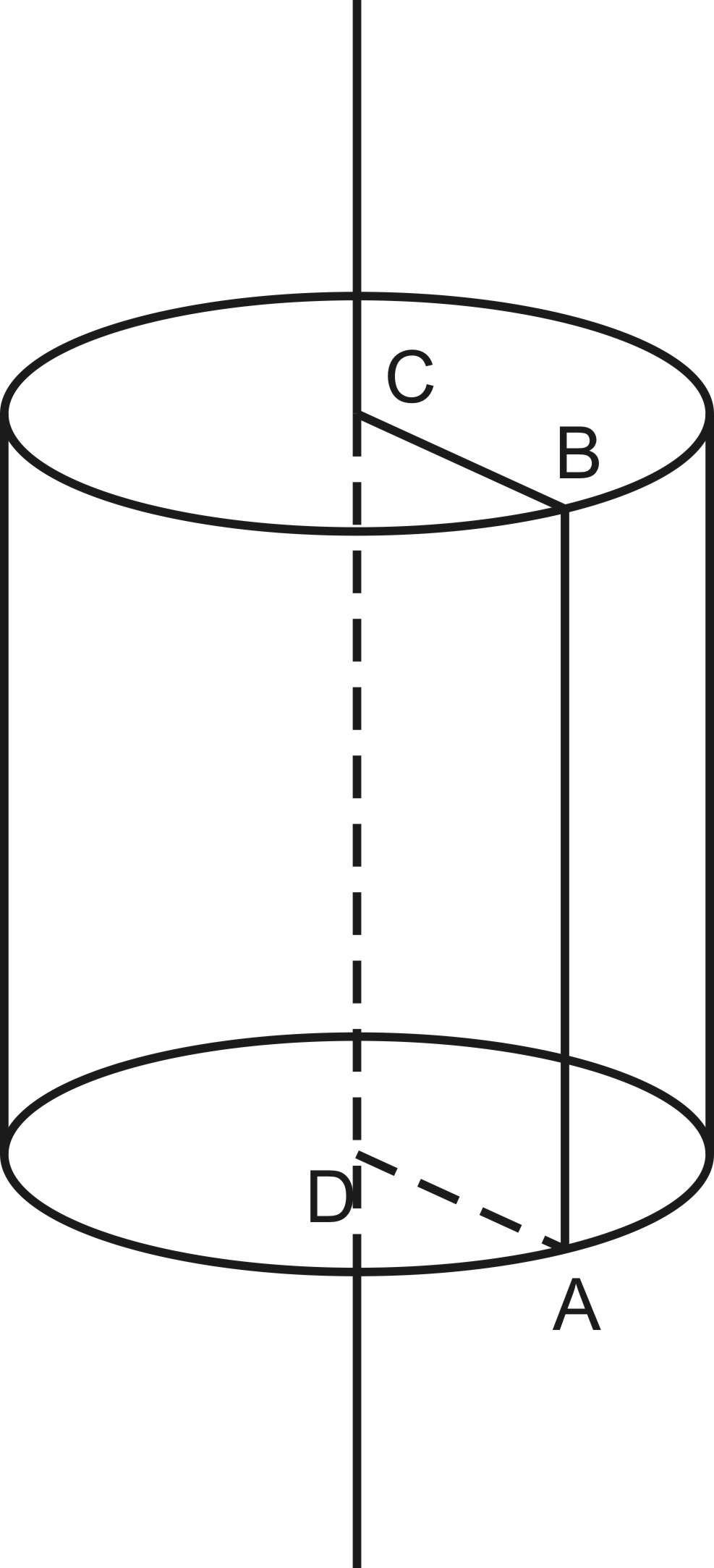Прямая СD₁- ось цилиндра.

Образующей цилиндра называется сторона AB прямоугольника ABCD,

при вращении прямоугольника она образует боковую поверхность

цилиндра.

Основания цилиндра – это круги, которые образуются от вращения

сторон DA и BC прямоугольника ABCD

Полная поверхность цилиндра состоит из двух его оснований и боковой

поверхности.

Высота цилиндра – отрезок перпендикуляра к основаниям цилиндра,

заключенный между этими основаниями.

Осевое сечение цилиндра - прямоугольник( MNPQ), полученный при

пересечении плоскости, проходящей через ось цилиндра

перпендикулярно его основаниям.

Развертка боковой поверхности цилиндра - прямоугольник, длина одной из сторон которого равна высоте цилиндра, а длина другой стороны – длине окружности основания цилиндра.

Сечения цилиндра плоскостью 4

1.Сечение, проходящее через две образующие цилиндра есть

прямоугольник (KFEL). Оно параллельно оси цилиндра.

2. Сечение, параллельное основаниям цилиндра, есть круг.

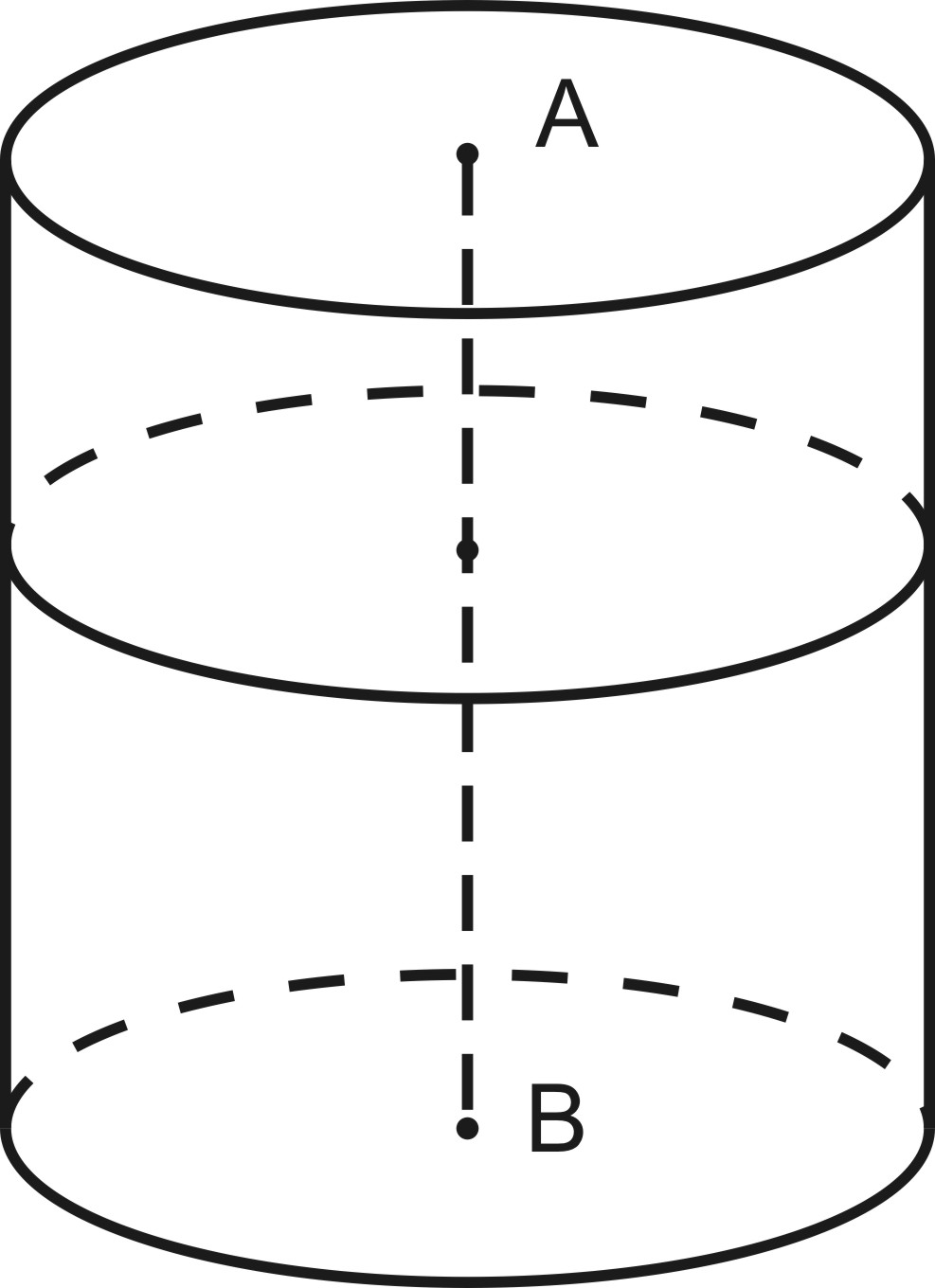
3. Cечение, не параллельное основаниям цилиндра и не пересекающее его основания есть эллипс.

Эллипс- это множество точек плоскости сумма расстояний от которых до двух заданных точек этой плоскости есть величина постоянная.

Покажем, что сечение, не параллельное основаниям цилиндра и не пересекающее его основания есть эллипс.

Пусть плоскость α пересекает поверхность цилиндра по некоторой линии L. Рассмотрим два шара, радиусы которых равны радиусам основания цилиндра, касающиеся поверхности цилиндра и плоскости .Точки касания c плоскостью обозначим F₁ и F₂. Линии пересечения поверхности цилиндра и шара обозначим L₁ и L₂. Выберем любую точку x линии пересечения L и проведем через нее образующую цилиндра. Обозначим длину этой образующей между точками пересечения A и B c линиями L₁ и L₂ 2a.

По теореме о касательных, проведенных из одной точки к сфере будем иметь:

xA = x F₁, xB = x F₂ . Cложим последние два равенства, получим

x F₁ + x F₂ = xA + xBAB =2a. Таким образом, сумма расстояний от двух заданных точек F₁ и F₂ до произвольной точки линии L есть величина постоянная.

Значит, линия L – эллипс. Доказательство закончено.

Прямой круговой конус = 5

Определение

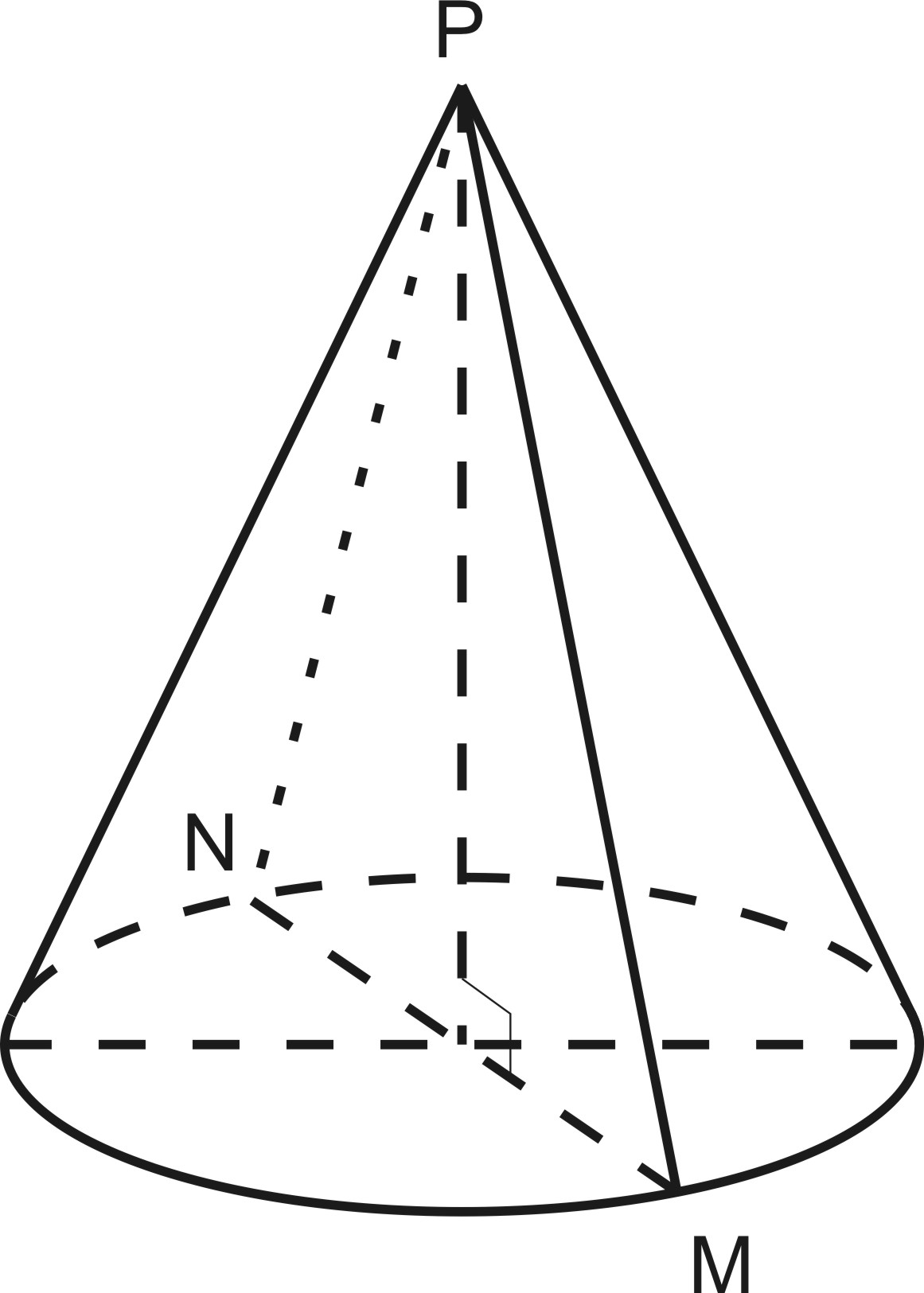
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг прямой, содержащей его катет.

Прямая СA- ось конуса.

Вершина конуса - это вершина A треугольника ABC.

Образующей конуса называется гипотенуза (сторона AB ) прямоугольного треугольника ABC, при вращении прямоугольного треугольника она образует боковую поверхность конуса.

Основания конуса – это круг, который образуется от вращения

стороны BC прямоугольного треугольника ABC.

Полная поверхность конуса состоит из его основания и боковой

поверхности.

Высота конуса – отрезок перпендикуляра из вершины конуса к плоскости

основания.

Осевое сечение конуса- треугольник (MNP), полученный при

пересечении плоскости, проходящей через ось конуса

перпендикулярно его основанию( рис. 160).

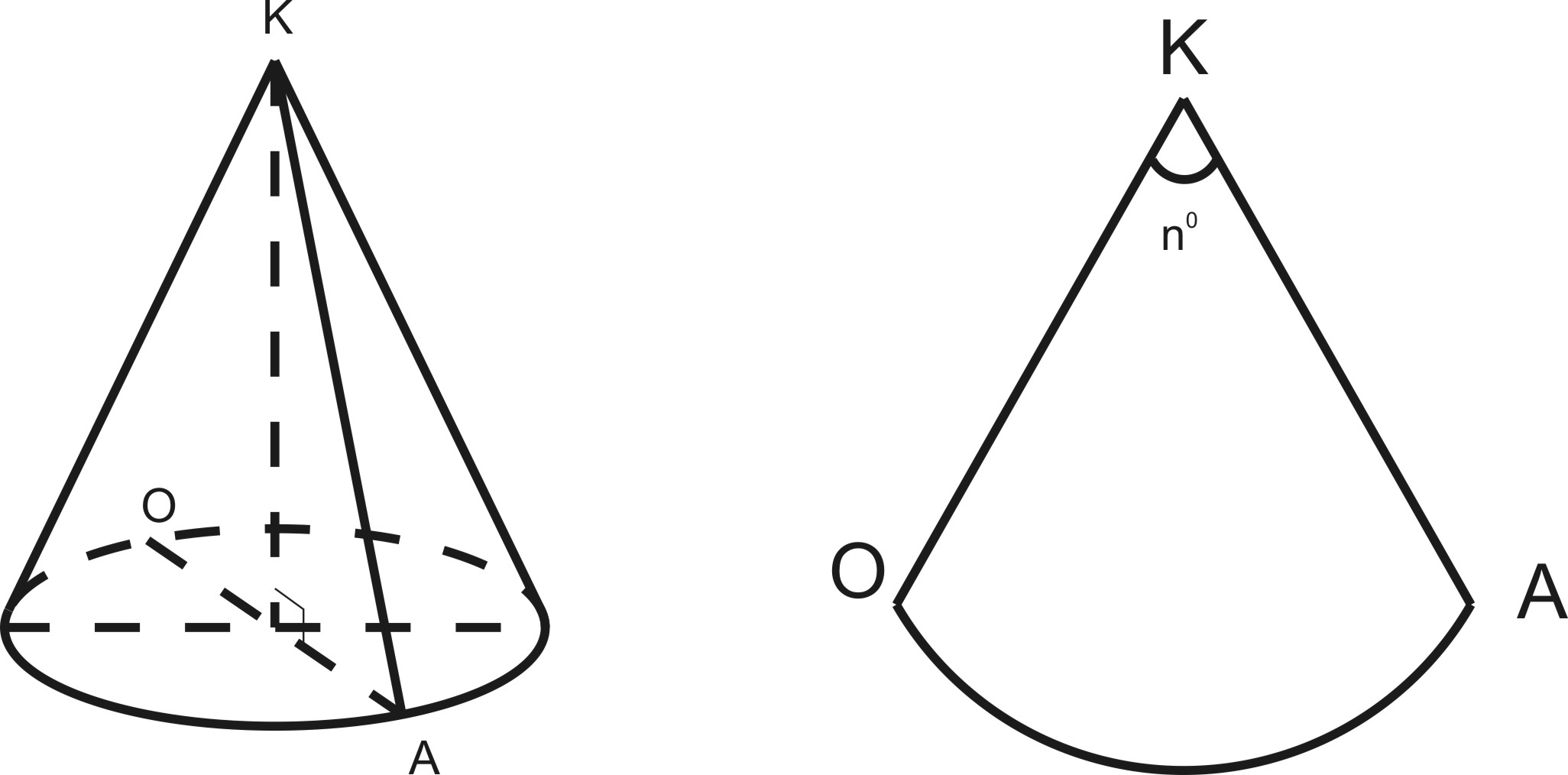
Развертка боковой поверхности конуса – есть круговой сектор

радиус которого равен образующей конуса, а длина

дуги сектора – длине окружности основания конуса:

L=ОA, =2πR, .

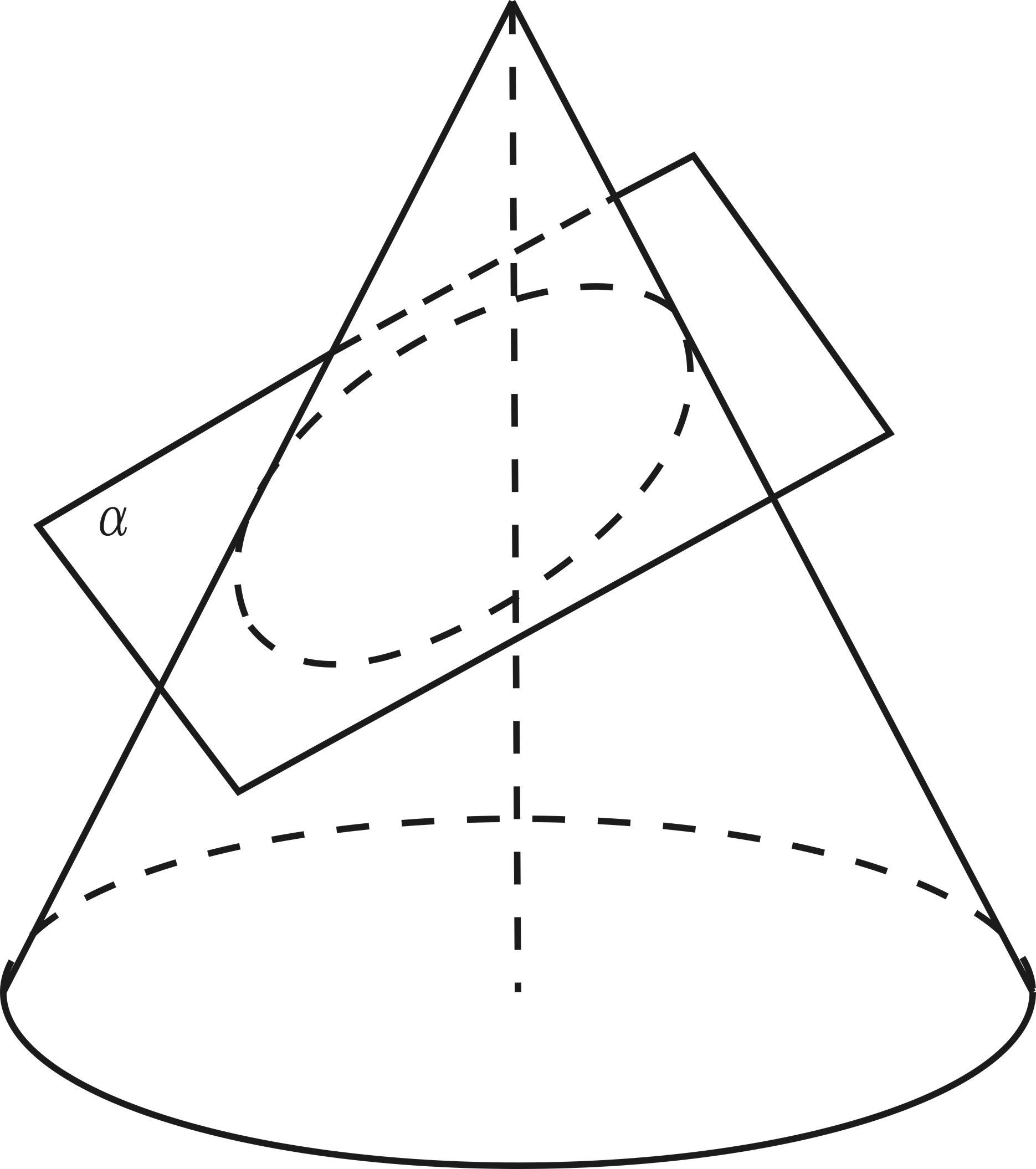
Сечения конуса плоскостью = 6

1.Осевое сечение конуса- треугольник), полученный при

пересечении плоскости, проходящей через ось конуса

перпендикулярно его основанию.

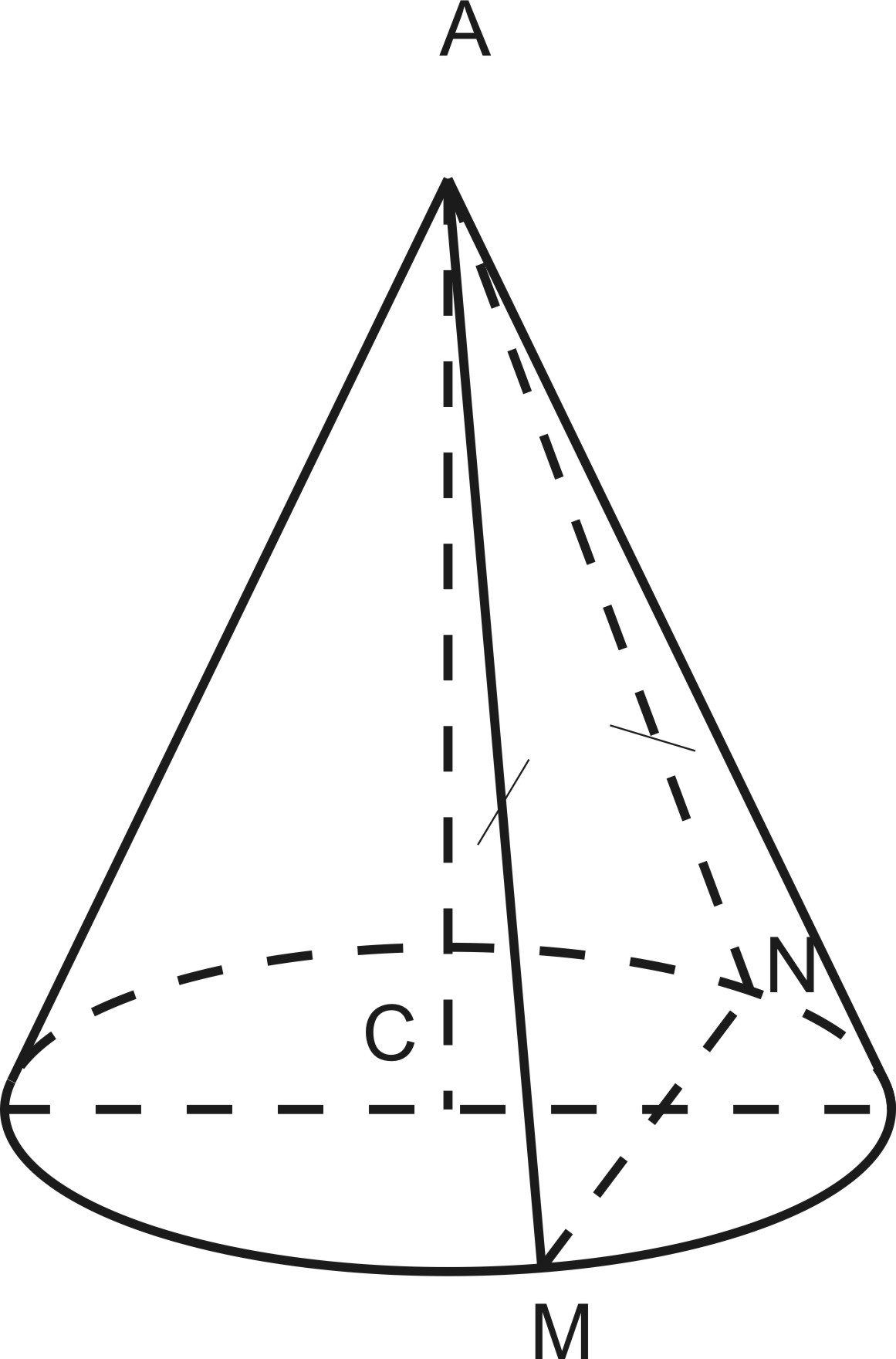
2. Сечение, проходящее через две образующие конуса , есть

равнобедренный треугольник .

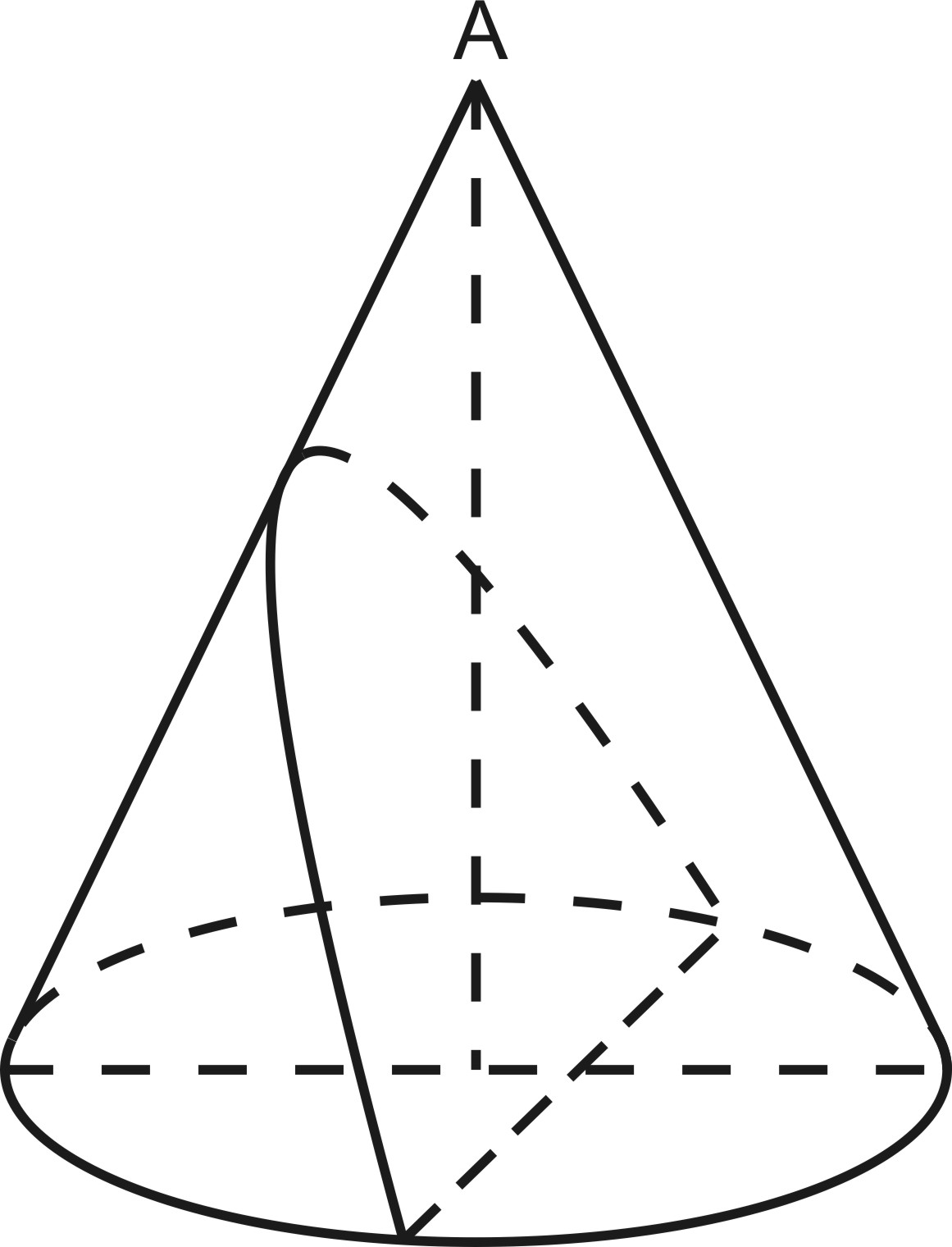
3. Сечение, параллельное только одной образующей конуса, есть парабола.

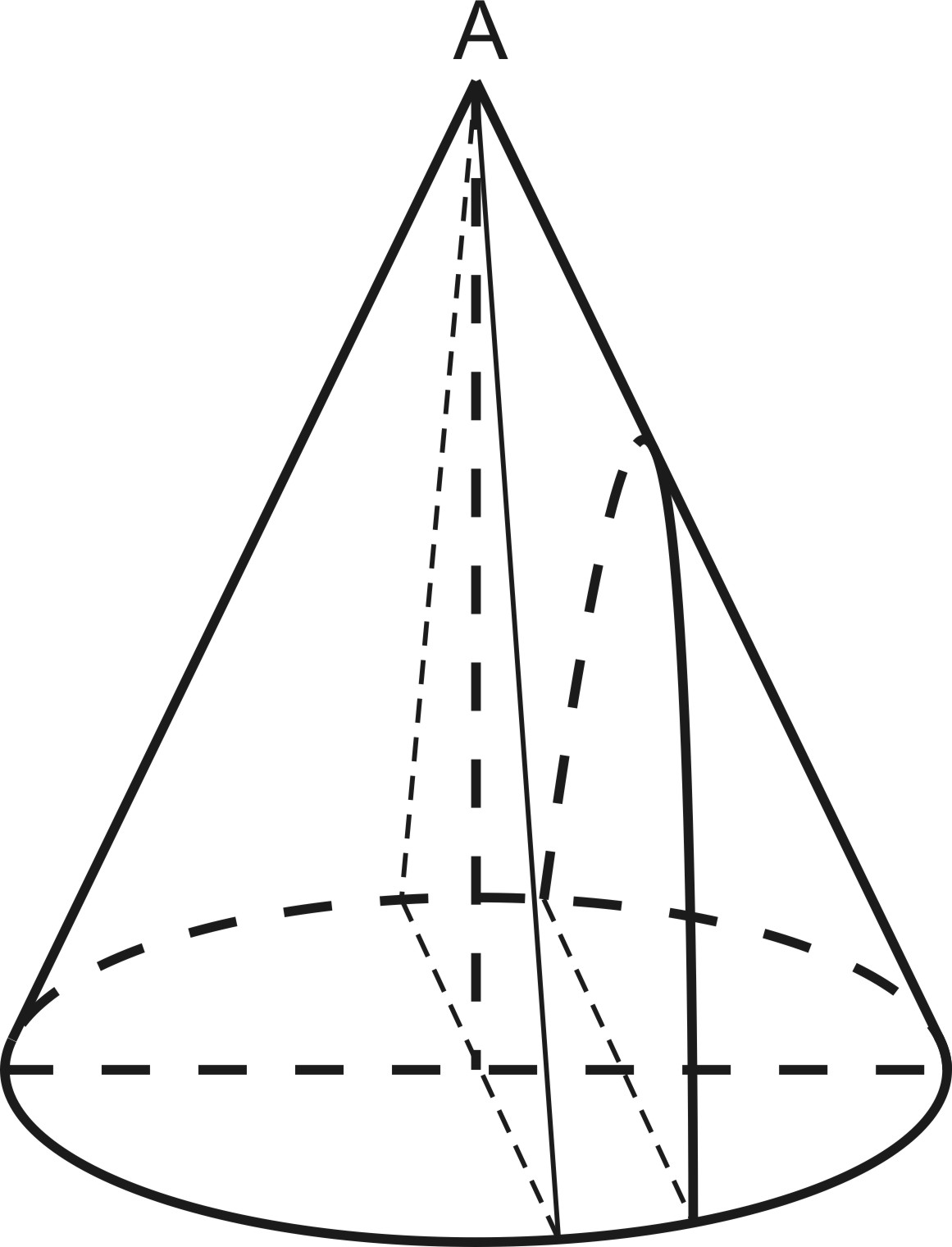
4. Сечение, параллельное двум образующим конус , есть гипербола.

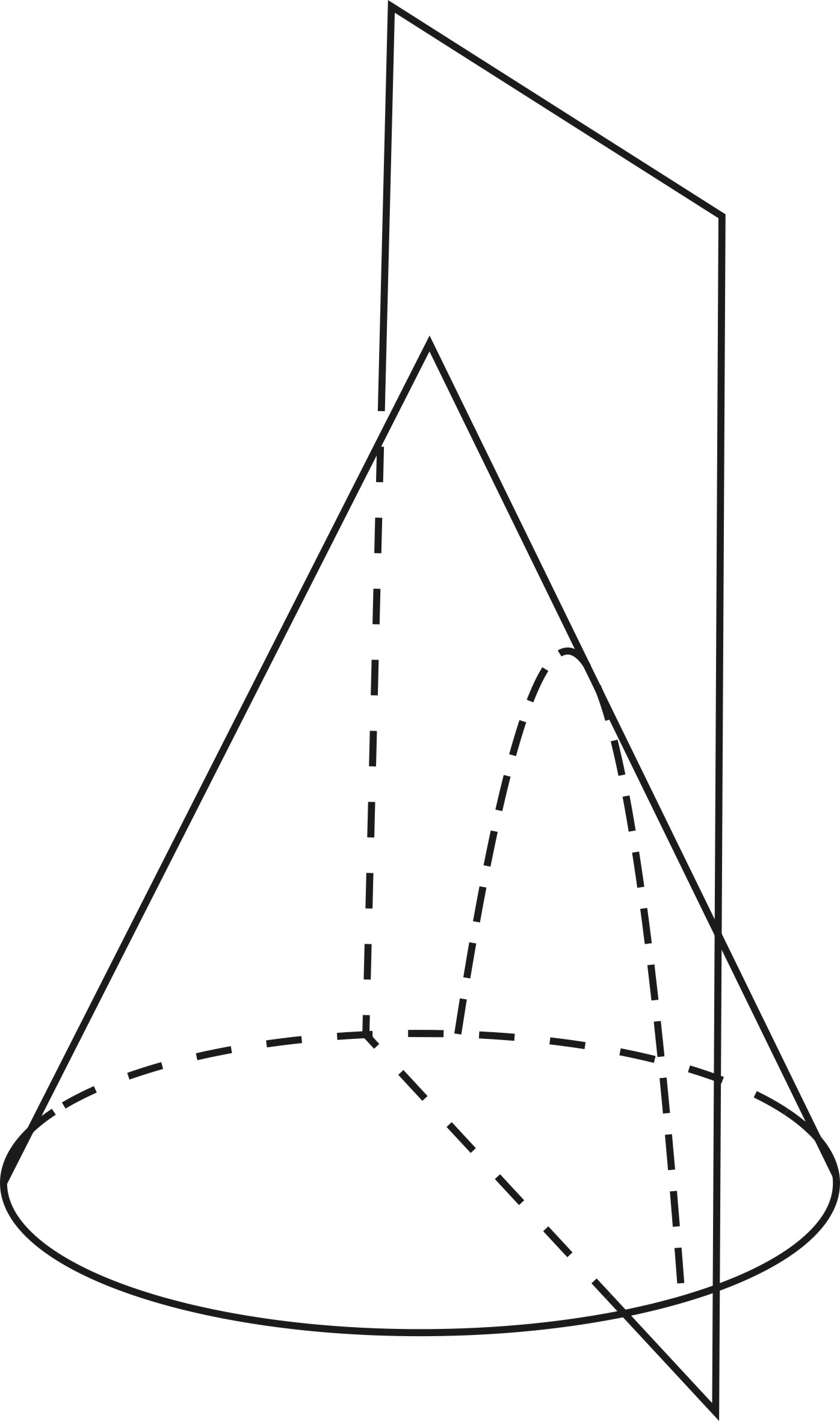
5. Сечение, не параллельное основанию и пересекающее все образующие конуса есть эллипс.