Усеченный конус

Определение

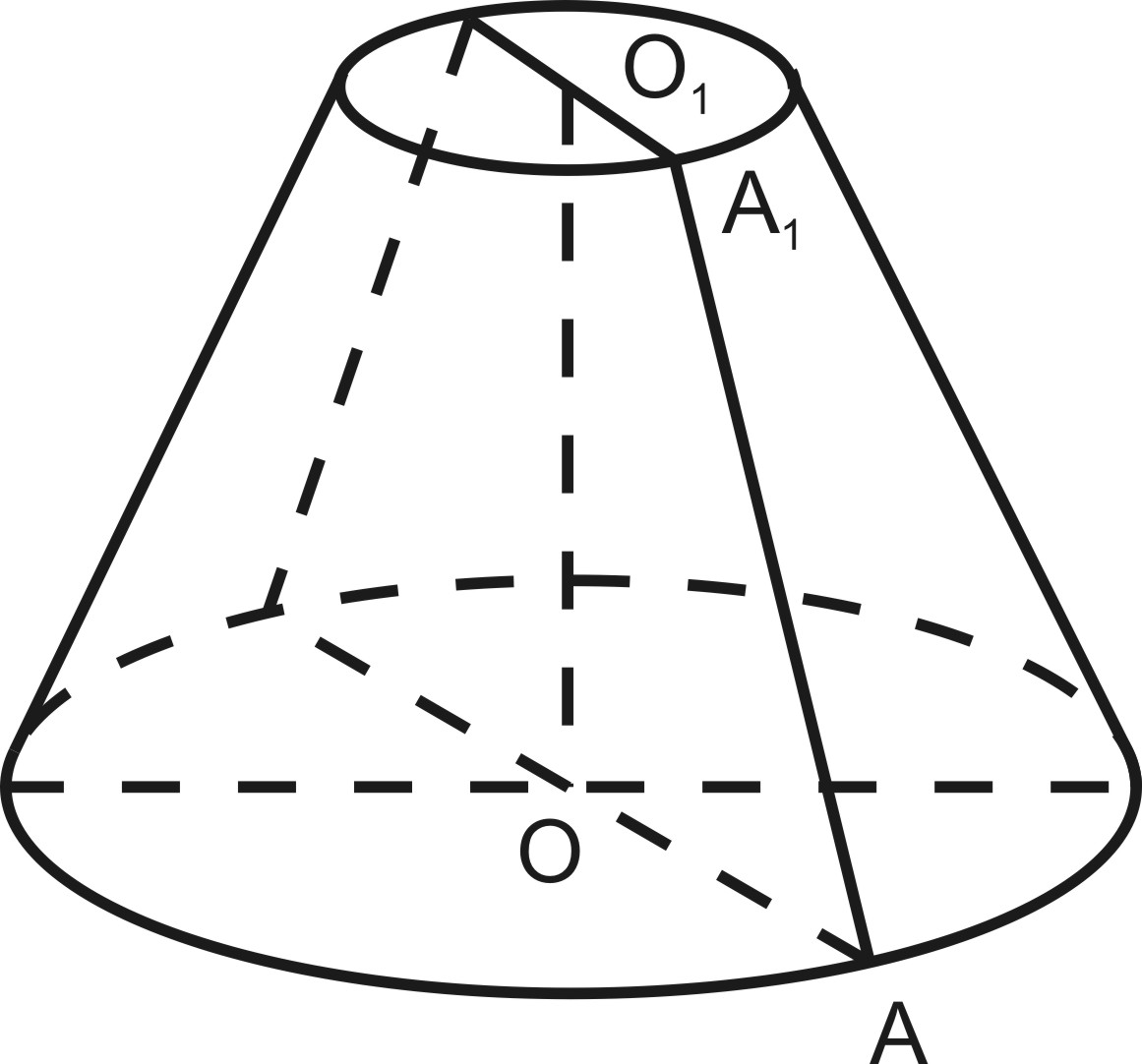
Усеченным конусом называется часть конуса, заключенная между основанием и плоскостью, параллельной основанию( рис.166).

AA₁- образующая, OO₁- высота, круги с центрами O и O₁, радиусами R и r - основания .

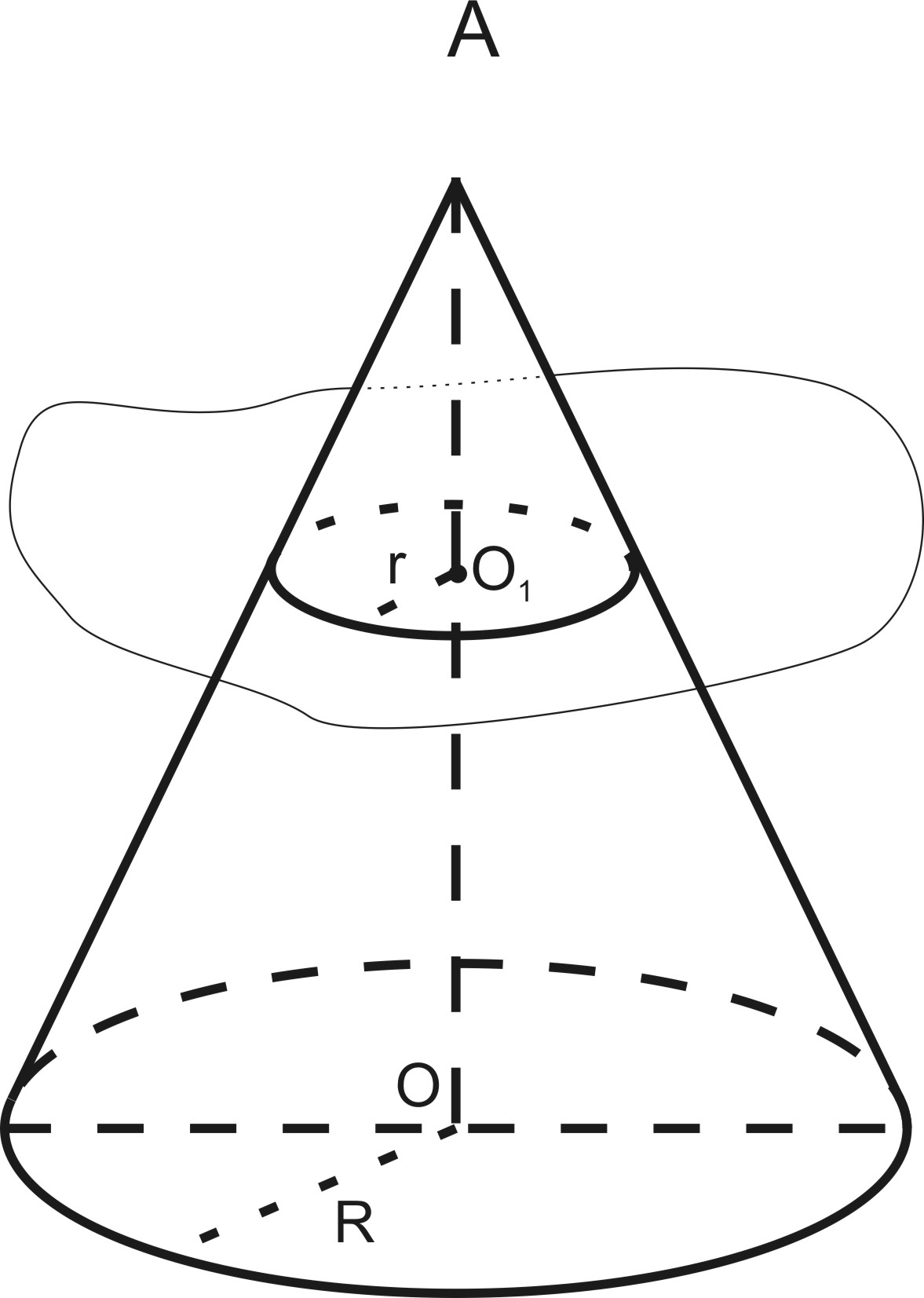
Осевое сечение усеченного конуса – равнобедренная трапеция, полученная при пересечении плоскости, проходящей через ось усеченного конуса

перпендикулярно его основанию).

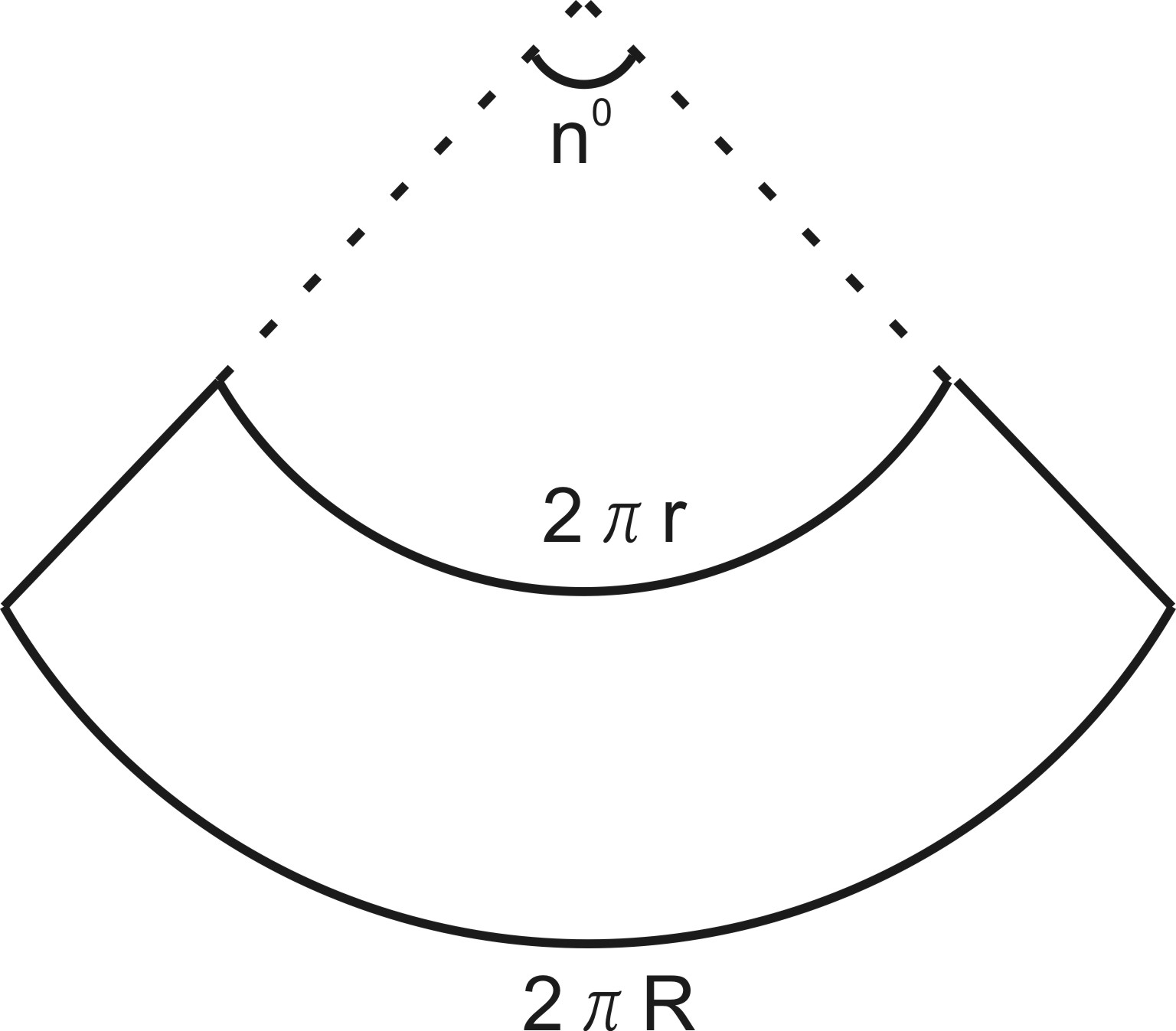
Развертка боковой поверхности усеченного конуса- часть кругового кольца.

Чтобы получить развертку боковой поверхности усеченного конуса, дополним

его до полного конуса и сделаем развертку полного конуса, а затем рассмотрим

на этой развертке развертку конуса с тем же центральным углом и меньшим радиусом, получим часть кольца

Сфера и шар. Элементы сферы и шара

Определения

1.Сферой называется множество всех точек пространства, находящихся на положительном расстоянии R от данной точки.

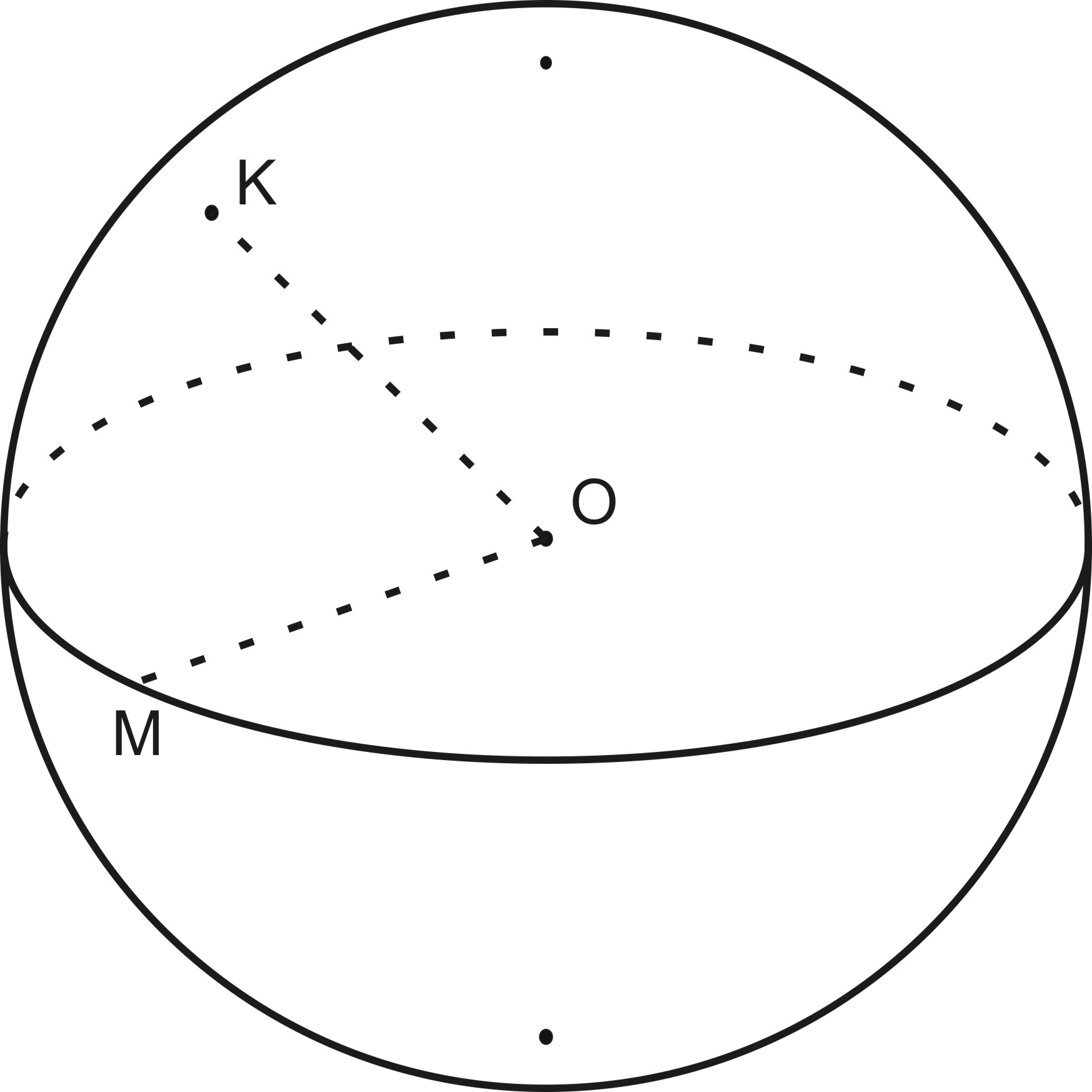
2.Центр сферы – данная точка O (рис.168), отрезок OM –радиус сферы.

Любой отрезок, соединяющий центр сферы с точкой сферы называется радиусом сферы.

3.Шаром называется множество всех точек пространства, находящихся на расстоянии, не больше положительного R от данной точки или

шар – это часть пространства, ограниченная сферой.

Радиус шара – это радиус ограничивающей его сферы.

Шар можно получить при вращении полукруга вокруг оси, которая содержит диаметр полукруга.

Отрезок, соединяющий две точки сферы, называется хордой сферы.

Хорда, проходящая через центр сферы называется диаметром сферы.

Уравнение сферы

Пусть задана прямоугольная система координат. Составим уравнение сферы с центром в точке S(a; b; c) и радиусом R.

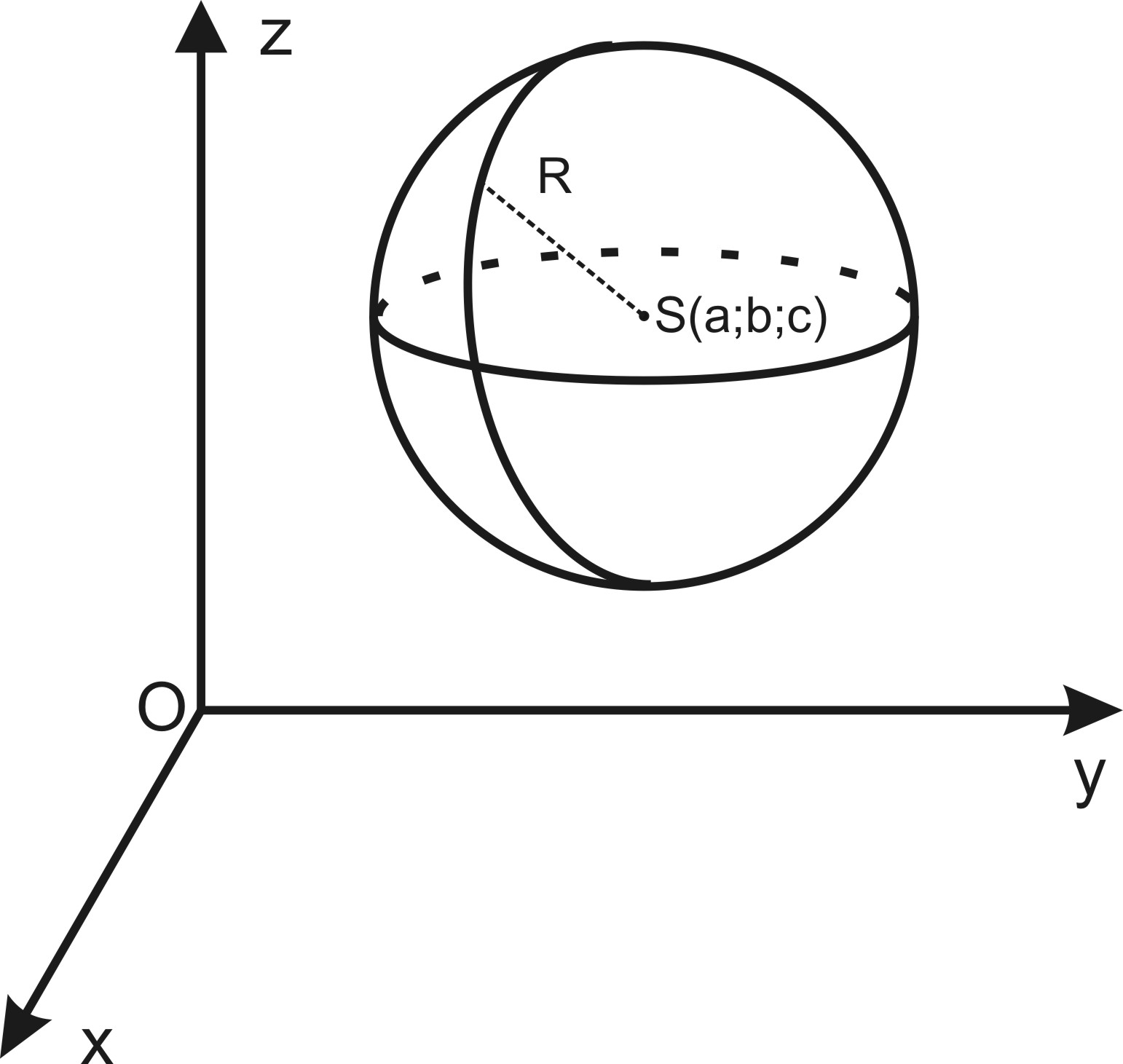
Для каждой точки M ( x;y;z), принадлежащей сфере и только для таких точек, выполняется равенство:

SM = R.

Пользуясь формулой расстояния между двумя точками, получим

(x-a) ² +( y- b ) ² + (z - c ) ² = R ² (1) .

Уравнение (1) и есть уравнение сферы с центром в точке (a; b; c) и радиусом R.

Если a=b=c=0, то получим уравнение сферы с центром в начале координат

x-² +y ² + z ² = R ² .

Сечение шара плоскостью

Рассмотрим сферу с центром в точке O и плоскость α .

Проведем ОС α. Пусть OC = d.

Если d > r, то сфера и плоскость общих точек не имеют.

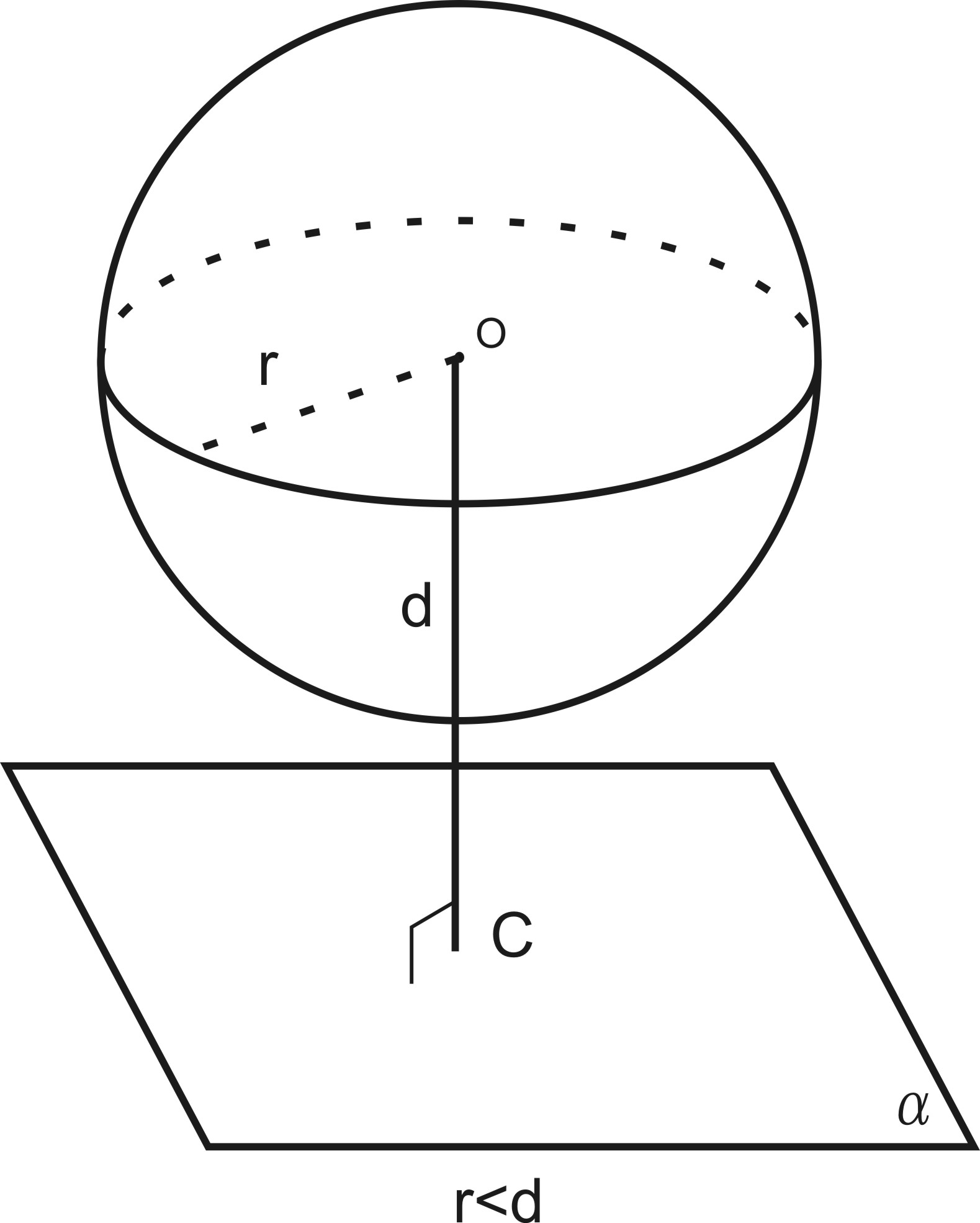
Если d < r, то сфера и плоскость имеют общие точки.

Теорема

Сечение сферы плоскостью – окружность.

Доказательство

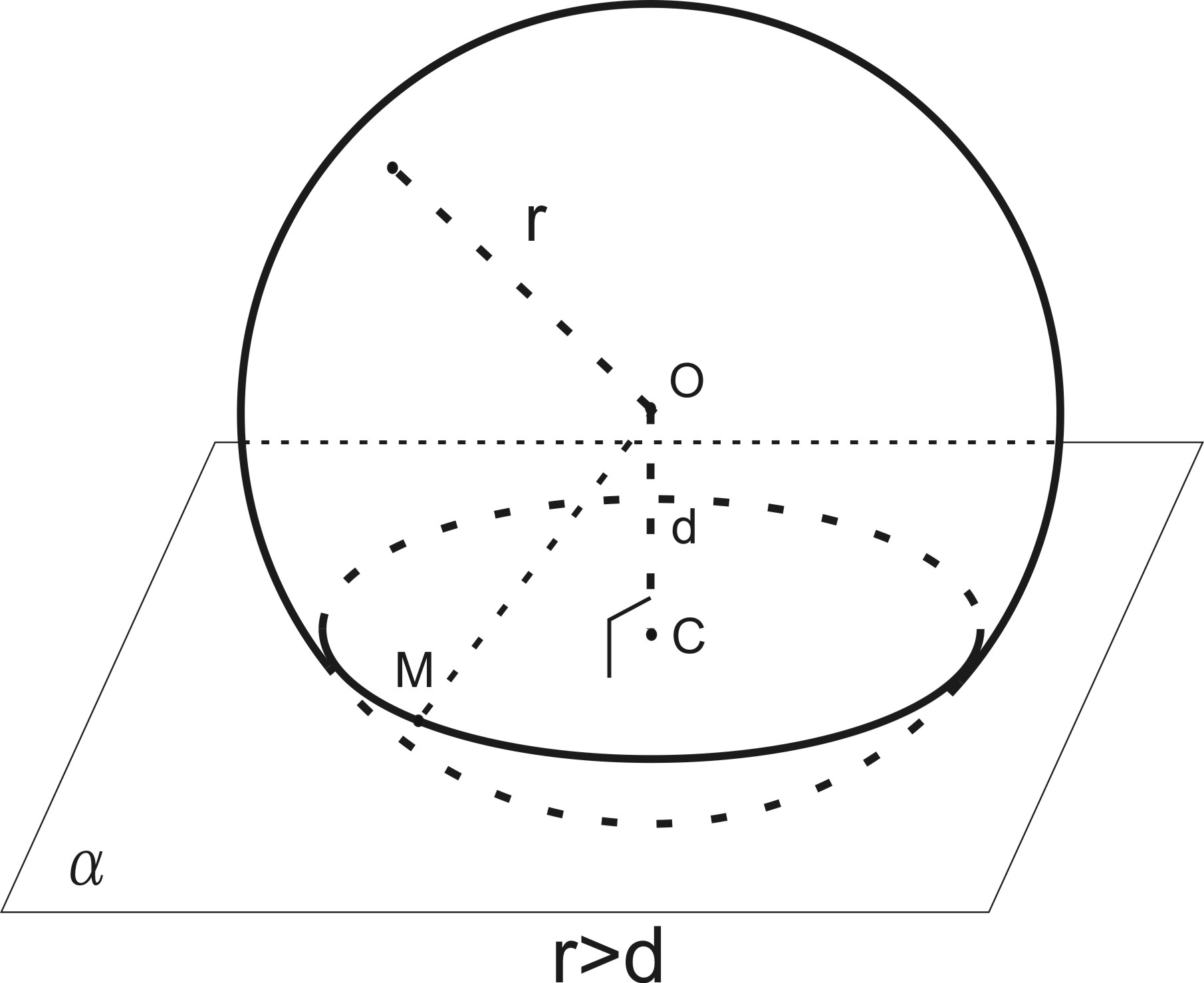
Пусть M – любая точка пересечения сферы с плоскостью α ( рис.170). Соединим ее с точкой С и проведем радиус OM. По определению перпендикуляра к плоскости ОС СM.

По теореме Пифагора CM = , где OC = d, r – радиус сферы.

Величины r и d – постоянные, следовательно, для любой точки пересечения сферы и плоскости расстояние до точки C есть величина постоянная, следовательно, по определению окружности – эта линия есть окружность.

Доказательство закончено.

Следствие 1

Сечение шара плоскостью есть круг.

Следствие 2

Сечения шара плоскостью, равноудаленные от центра, равны

Следствие 3

Сечения шара плоскостью тем больше, чем ближе оно расположено к центру.

Определение1

Сечения шара плоскостью, проходящей через центр шара, называется большим кругом, а его окружность – окружностью большого круга.

Определение2

Точки пересечения сферы с диаметром, перпендикулярным большому кругу, называются полюсами сферы.

Следствие 4

Два больших круга пересекаются по диаметру.

Следствие 5

Сечением шара плоскостью является точка, если расстояние от центра шара до плоскости равно радиусу шара.