
- •Оглавление
- •§1. Экспериментальные основы квантовой механики
- •§2. Классическое и квантовое описание системы
- •[§3.] Принцип неопределенности
- •[§4.] Полный набор динамических переменных
- •[§5.] Постулаты квантовой механики
- •§6. Роль классической механики в квантовой механике
- •[§7.] Волновая функция и ее свойства
- •[§8.] Принцип суперпозиции состояний
- •§9. Понятие о теории представлений
- •[§10.] Операторы в квантовой механике
- •Транспонированный оператор
- •[§11.] Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного)* спектра
- •§12. Среднее значение измеряемой величины
- •§13. Вероятность результатов измерения
- •§14. Коммутативность операторов и одновременная измеримость физических величин (1/2*)
- •[§15.] Операторы координаты , импульса , момента импульса , энергии .
- •§16. Решение задачи на собственные функции и собственные значения для оператора
- •§17. Решение задачи на собственные функции и собственные значения для оператора .
- •§ 18. Вычисление коммутаторов, содержащих операторы (и *).
- •[§ 19.] Волновое уравнение
- •§ 20 Производная оператора по времени
- •§ 21 Интегралы движения в квантовой механике
- •§22. Флуктуации физических величин (1/2*)
- •§ 23. Неравенства Гайзенберга. (1/2*)
- •[§ 24.] Оператор Гамильтона различных систем
- •§ 25. Стационарное состояние различных систем
- •[§ 26.] Решение волнового уравнения в случае свободной материальной точки
- •§ 27. Решение волнового уравнения в случае бесконечно глубокой потенциальной ямы
- •[§ 28.] Собственный механический момент (спин)
- •§ 29*. Операторы и и их свойства
- •§ 30. Спиновая переменная волновой функции
- •§ 31. Матрицы Паули (и их свойства)*.
- •§ 32. Принцип тождественности
- •§33. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: нулевое и первое приближения
- •A.1. Стационарная теория возмущений в случае невырожденного дискретного энергетического спектра: второе приближение
- •A.2. Критерий применимости теории возмущений
- •A.3. Стационарная теория возмущений в случае близких энергетических уровней.
- •Экзаменационные вопросы по курсу "Квантовая теория".
- •Экзаменационные задачи по курсу "Квантовая теория".
- •Экзаменационные вопросы по курсу "Квантовая теория".(минимум)
- •Экзаменационные задачи по курсу "Квантовая теория".(минимум)
- •Решения задач по курсу "Квантовая теория"
§ 20 Производная оператора по времени
Пусть средняя от величины
![]() ,
тогда
,
тогда
![]() .
.
Ставим в соответствие величине
оператор
,
тогда величине
![]() ставим в соответствие
ставим в соответствие
![]() .
.
Распишем:
![]() {ограничение
{ограничение
![]() }
}![]() {
и соотношение
{
и соотношение
![]() ,
,
![]() }=
}=
=![]() ={
={![]() }=
}=![]() => {распишем квадратную скобку операторов:
=> {распишем квадратную скобку операторов:
![]() ,
но
,
но
![]() ,
тогда
,
тогда
![]() }
}
В классической механике
![]() .
[]-скобки Пуассона.
.
[]-скобки Пуассона.
В квантовой механике существует связь:
![]()
В пределе
имеем
![]() .
.
В квантовой механике большинство операторов физических величин явно не зависят от времени и их частные производные равны 0.
§ 21 Интегралы движения в квантовой механике
В классической механике
![]() ,
где
,
где
![]() ,
тогда A – интеграл
движения.
,
тогда A – интеграл
движения.
В квантовой механике, чтобы величина
,
которой ставится в соответствие оператор
,
была интегралом движения нужно, чтобы
![]() .
.
Для того чтобы физическая величина
сохранялась, необходимо и достаточно,
чтобы
![]() .
.
т. к.
 ,
то
,
то
 -значение
момента импульса сохраняется, т. е.
является интегралом движения.
-значение
момента импульса сохраняется, т. е.
является интегралом движения. .
.
 - интеграл движения.
- интеграл движения.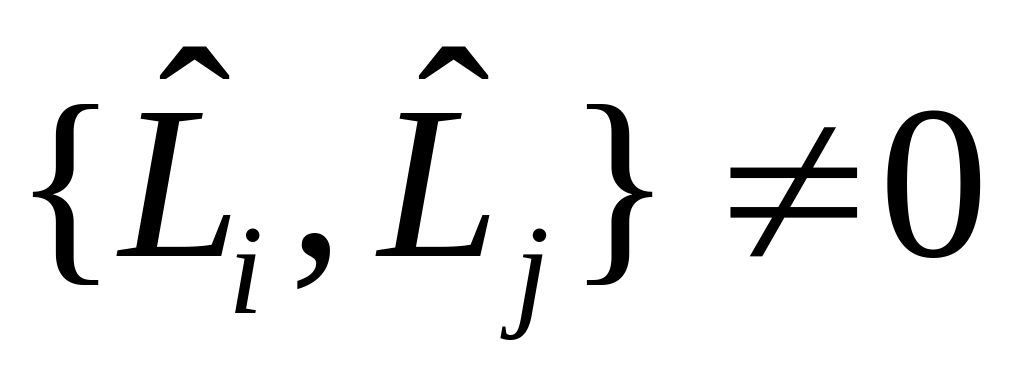 .
Отсюда следует. Что различные компоненты
момента импульса одновременно не
измеримы. А измерима только одна проекция
.
.
Отсюда следует. Что различные компоненты
момента импульса одновременно не
измеримы. А измерима только одна проекция
. .
Квадрат импульса одновременно измерим
с любой компонентой момента импульса.
.
Квадрат импульса одновременно измерим
с любой компонентой момента импульса. ,
тогда импульс не является интегралом
движения.
,
тогда импульс не является интегралом
движения.
§22. Флуктуации физических величин (1/2*)
Пусть есть
- физическая величина, которая при
измерении с вероятностью Wi
дает величину
![]() ,
тогда мы можем говорить о среднем
,
тогда мы можем говорить о среднем
![]() и о дисперсии
и о дисперсии
![]() ,
где
,
где
![]() .
.
Мы вводили флуктуацию
![]() ,
,
отклонение величины от ее среднего значения.
![]()
Перенесем все это на язык квантовой механики, т. к. физической величине мы ставим в соответствие .
Можно показать, что
![]() .
.
Неравенство Коши-Шварца: Оно справедливо и для функциональных пространств, в том числе и для гильбертова пространства, которое рассматривается в квантовой механике.
![]()
Для двух векторов оно имеет вид
![]()
имеет смысл тот, что
![]() .
.
![]() ,
,
![]() .
.
Теперь если обозначить
![]() ,
,
![]() ,
тогда будем также рассматривать
статистическое усреднение
,
тогда будем также рассматривать
статистическое усреднение
![]() .
Отсюда получим из неравенства Коши-Шварца:
.
Отсюда получим из неравенства Коши-Шварца:
![]()
Теперь если определить
![]() .
К тому же по определению из
имеем
.
К тому же по определению из
имеем
![]() ,
тогда
,
тогда
![]() .
Из этого следует, что
.
Из этого следует, что
![]() .
.
В случае квантовой механики заменяем на , тогда
![]() .
.
Задача. Для стационарного
состояния частицы в бесконечно глубокой
потенциальной яме найти
![]()
Решение. Будем считать, что в.ф. для данной системы уже получены (см. §27).
Согласно определению:
![]() (22.1)
(22.1)
Поэтому остается рассчитать
![]()
а) В случае
![]() числа
числа
![]() находится вычислениями
находится вычислениями


Подставляя полученные значения в (22.1),
получаем
![]()
б)Для оператора
![]()
Среднее значение будет равно
![]()
![]()
Подставим в (22.1) и получим
![]()
§ 23. Неравенства Гайзенберга. (1/2*)
Канонически сопряженные величины одновременно неизмеримы – это принцип неопределенности.
Под канонически сопряженными понимаем
величины
![]() и
и
![]() .
.
![]()
![]()
В квантовой механике для операторов
![]() и
и
![]() ,
которые поставлены в соответствие
канонически сопряженным величинам
имеем
,
которые поставлены в соответствие
канонически сопряженным величинам
имеем
![]() .
.
Более того
![]() ,
а сам коммутатор
,
а сам коммутатор
![]() имеет вид оператора
имеет вид оператора
![]() .
.
Это можно записать в виде
![]() .
.
Если
![]() ,
то
,
то
![]() ,
тогда
,
тогда
![]() ,
где
,
где
![]() .
.
(*) Вывод:
![]()
![]() ,
т.к.
,
т.к.
![]() и
и
![]() есть числа.
есть числа.
Обозначим
![]() .
Здесь
.
Здесь
![]() - единичный оператор.
- единичный оператор.
Тогда из
получим
![]() (*)
(*)
Введем обозначение

Подставим это в неравенство Коши-Шварца, тогда
![]()
Используем эрмитовость операторов
![]() ,
,
![]() ,
,
тогда
![]() .
.
Поделим левую и правую части на
![]() , тогда
, тогда

Используем определение среднего
![]() ,
,
тогда
![]() .
.
Или
![]()
Операторы
и
![]() не коммутируют, тогда
не коммутируют, тогда
![]() .
.
Первое слагаемое обозначим
![]() ,
,
![]() .
.
Второе слагаемое
![]() .
.
Оператор
дает чисто вещественное число, а
![]() дает чисто мнимое число.
дает чисто мнимое число.
Тогда
![]() ,
,
где
![]() .
.
![]() .
.
Окончательно
![]() .
.
В полученном неравенстве математически заложен принцип неопределенности Гайзенберга.
Если величина измерена точно, то
![]() ,т.е.
,т.е.
![]() .
.
Если
,
то величина A измерена
точно и
![]() ,
но тогда для
,
но тогда для
![]() ,
т. к.
.
Из этого следует, что канонически
сопряженная величина B
не измерима.
,
т. к.
.
Из этого следует, что канонически
сопряженная величина B
не измерима.
Когда измеряем величину
,
то получаем спектр значений
,
которые выходят с вероятностью
.
Для того чтобы
![]() необходимо чтобы система находилась в
состоянии
необходимо чтобы система находилась в
состоянии
![]() .
.
