Примеры

Пример 3.3

Построить вывод в ИП для формулы х А у (А(х у)), где А – формула, х и у – различные переменные, причем у не входит свободно в А.

В более традиционной (но менее точной) записи это высказывание имеет вид: х А(х) у А(у).

Решение

Строим вывод:

х А(х) А(у), (а)

это пример схемы аксиом (ип2);

у ( х А(х) А(у)), (б)

по правилу (Gen) из (а), структурное требование выполняется, так как (а) – не гипотеза (а аксиома ИП);

у ( х А(х) А(у)) ( х А(х) у А(у)), (в)

это пример схемы аксиом (ип12) (существенно, что х А(х) не содержит свободно у);

х А(х) у А(у) (г)

вытекает из (б) и (в) по правилу (MP).

Соответствующее дерево вывода имеет вид:

П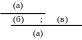 ример 3.4

Привести краткое обоснование пяти допустимых структурных правил вывода в ИП).

Решение

Правило 1 – из гипотезы A и ввиду А A по (MP) A А.

Правила 2 – 4 – тривиально допустимы. Вывод, обосновывающий секвенцию выше черты, обосновывает и секвенцию ниже черты;

Правило 5 – из B, A C по теореме о дедукции B А C. Отсюда и из Г А по правилу добавления Г, B А C; Г, B А. Применяя (MP), получим Г, B C.

Пример 3.5

Доказать логические правила техники естественного вывода в ИП (см. с. 59-60).

Решение

Приведем доказательства некоторых из правил (остальные доказываются аналогично).

-введение. Это есть в точности теорема о дедукции.

-удаление. Из данных выводов Г A, Г A B вывод для Г B получим с помощью (MP).

-введение. Имеем: Г A. Кроме того, A AB (это аксиома). По (MP) Г AB.

-удаление. Из данных Г,A C; Г,B C по теореме о дедукции Г A C и Г B C. Кроме того, (A C) ((B C) (AB C)) (это аксиома). Дважды применяя (MP), получим: Г AB C. По закону тождества (и правилу добавления) Г,AB AB. По (MP) Г,AB C.

-удаление. Из Г,A(y) C по теореме о дедукции следует, что Г A(y) C. По правилу обобщения Г y(A(y) C) (здесь существенно, что y не входит свободно в Г). Имеем аксиому y(A(y) C) ( y(A(y) C)). По (MP) Г y A(y) C. Аналогично x A(x) yA(y). Отсюда Г, xA(x) yA(y). Следовательно, по (MP) Г, xA(x) C.

-введение. Из Г, A В и Г, B A по теореме о дедукции Г A B, Г B A, Г (A B) (B A), что и означает по определению эквивалентности Г A B.

Пример 3.6

Доказать в ИП, что AB (A B).

Решение

Согласно -введению достаточно установить AB (A B) и (A B) AB.

Начнем с первой секвенции. Слева у нее стоит дизъюнкция, поэтому, разбирая случаи согласно - удалению, достаточно установить два факта:

A (A B) и B (A B).

Установим только первый, второй устанавливается симметрично. Для вывода отрицания (A B) достаточно допустить A B и вывести противоречие, т.е. использовать -введение. Противоречие будет состоять в выводе A и A. Итак, для вывода A (A B) с помощью -введения достаточно установить: A,A B A и A,A B A.

Первая секвенция выводима по закону тождества. Для вывода второй согласно -удалению достаточно показать: A,A,B A, что также следует из закона тождества.

Теперь установим: (A B) AB. Здесь наше рассуждение будет косвенным. Согласно -удалению достаточно установить: (A B)

(AB). А для этого согласно -введению следует, допустив (AB), вывести противоречие.

Мы докажем:

(A B),(AB) (A B) и (AB) A B.

Первая секвенция, очевидно, выводима по закону тождества. Вторую секвенцию получим по -введению. Достаточно вывести:

(AB) A и (AB) B.

Мы выведем первую секвенцию, вторая выводится симметрично. Используя - введение, достаточно вывести:

(AB),A (AB) и (AB),A AB.

Но первая из этих секвенций очевидна, а вторая получается с помощью -введения из (AB),A A.

Пример 3.7

Вывести AA.