4.6.4. Границы ошибки

Хотя уравнение (33) дает точный результат, еще показательнее получить границы для Р, выраженные посредством байесовского уровня Р*. Очевидной нижней границей для Р является сам уро­вень Р*. Кроме того, можно показать, что при любом Р* существует множество условных и априорных вероятностей, для которых эта граница достигается. Так что в этом смысле это точная нижняя гра­ница.

Еще интереснее задача определения точной верхней границы. Следующее соображение позволяет надеяться на низкую верхнюю границу: если байесовский уровень небольшой, то Р(|х) близка к единице для некоторого i, скажем i=m. Таким образом, подынте­гральное выражение в (33) будет приближенно 1—Р²(|х) 2(1—Р(|х)), и поскольку

Р*(е|х)=1-Р(|х), (34)

то интегрирование по х может дать уровень, в два раза превышающий байесовский, но являющийся все еще низким. Чтобы получить точ­ную верхнюю границу, мы должны определить, насколько большим может стать уровень Р ошибки правила ближайшего соседа для за­данного байесовского уровня Р*. Таким образом, выражение (33) вынуждает нас задаться вопросом, насколько малой может стать для заданной р(|х). Записав

,

мы можем получить границу этой суммы, минимизируя второй член при следующих ограничениях:

1) Р(|х)0;

2)

Несколько поразмыслив, мы видим, что минимизируется, если все апостериорные вероятности, кроме т-й, равны, и второе ограничение дает

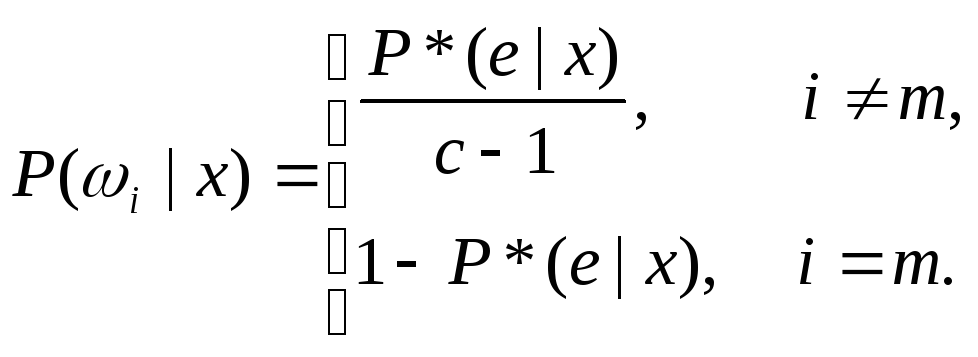(35)

Таким образом,

(1-P*(e|x))²+

и

1- 2P*(e|x)-P*²(e|x). (36)

Сразу же видим, что Р2Р*, поэтому можем подставить этот резуль­тат в (33) и просто опустить второй член выражения. Однако более точную границу можно получить на основании

так что

причем равенство сохраняется тогда и только тогда, когда диспер­сия Р*(е|х) равна нулю. Пользуясь этим результатом и подставляя соотношение (36) в (33), получаем желаемые границы

Р*РР*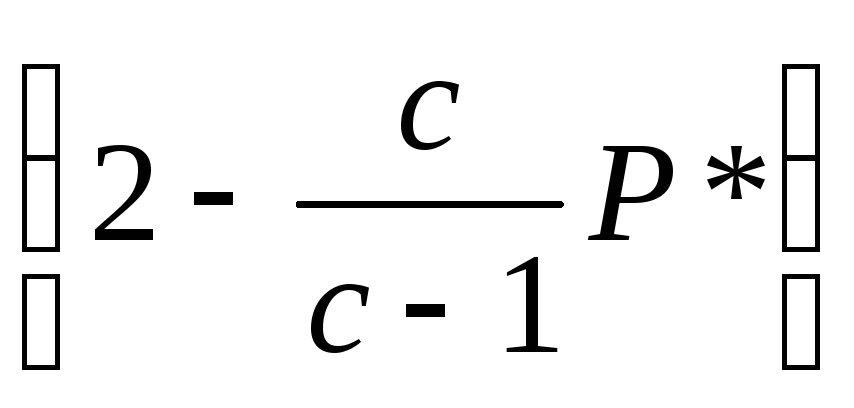. (28)

Легко показать, что такая верхняя граница достигается в слу­чае так называемой нулевой информации, в котором плотности рас­пределения p(х|) тождественны, так что Р(|х)=р() и Р*(е|х) не зависит от х. Таким образом, границы, заданные (28), являются максимально близкими в том смысле, что для любой Р* существуют условные и априорные вероятности, для которых эти границы до­стигаются. На рис. 4.4 графически представлены эти границы. Байесовский уровень Р* может находиться в любом месте между О и (с—1)/с. Границы сходятся в этих двух крайних точках. Когда байесовский уровень мал, верхняя граница превышает его почти в два раза. В общем значение ошибки правила ближайшего соседа должно находиться в заштрихованной области.

Поскольку Р всегда меньше или равна 2Р*, то, если имеется бе­сконечный набор данных и используется сложное решающее пра­вило, можно по крайней мере в два раза сократить уровень ошибки. В этом смысле по крайней мере половина классифицирующей ин­формации бесконечного набора дан­ных находится по соседству.

Естественно задаться вопросом, насколько хорошо правило бли­жайшего соседа в случае конечного числа выборок и как быстро ре­зультат сходится к асимптотичес­кому значению. К сожалению, от­веты для общего случая неблаго­приятны. Можно показать, что сходимость может быть бесконечно медленной и уровень ошибки Р_n(е) даже не должен монотонно убывать с ростом п. Так же, как это про­исходит с другими непараметрическими методами, трудно получить какие-либо еще результаты, кроме асимптотических, не делая даль­нейших допущений о вероятностных свойствах.

Рис. 4.4. Границы ошибки правила ближайшего соседа