Глава 5 линейные разделяющие функции

5.1. Введение

В гл. 3 предполагалось, что вид рассматриваемых распределений вероятностей известен, и с помощью выборок производилась оценка их параметров. В данной главе известным будет считаться вид раз­деляющих функций, и выборки будут использоваться для оценки значений параметров классификаторов. Исследованию подлежат различные процедуры, применяемые для определения разделяющих функций, имеющие как статистический, так и нестатистический характер. Однако ни для одной из них не требуется, чтобы был из­вестен вид рассматриваемых распределений вероятностей, и в этом смысле все их можно считать непараметрическими.

В данной главе будут рассматриваться разделяющие функции, линейные либо по компонентам вектора х, либо по некоторому дан­ному множеству функций от х. Линейные разделяющие функции наиболее удобны с точки зрения аналитического исследования. Как было показано в гл. 2, они могут быть оптимальными, если рассматриваемые распределения согласованы. Даже когда они не оптимальны, может быть следует пренебречь некоторыми качествами ради выигрыша в простоте.

Вычислительный процесс значительно упрощается при исполь­зовании линейных разделяющих функций, и классификатор опреде­ленной структуры представляется наиболее подходящим средством для реализации в качестве машины специального назначения.

Линейный дискриминант Фишера является моделью в принятом нами подходе. Задача определения линейной разделяющей функции будет сформулирована как задача минимизации некоторой функции критерия. Вполне оправданным является использование выбороч­ного риска в качестве критерия для задач классификации, т. е. сред­них потерь при классификации множества конструктивных выборок. Однако поскольку получение линейного дискриминанта, дающего минимальный риск, представляется достаточно трудным, в данной главе будет исследовано несколько аналогичных функций крите­рия, имеющих более простые аналитические выражения. Наиболь­шее внимание уделяется исследованию сходимости различных про­цедур градиентного спуска для минимизации этих функций. Сходст­во многих процедур иногда затрудняет выделение очевидных различий между ними. По этой причине в изложение материала вклю­чена сводка основных результатов, данная в табл. 5.1 в конце разд. 5.10.

5.2. Линейные разделяющие функции и поверхности решений

5.2.1. Случай двух классов

Разделяющая функция, представляемая линейной комбинацией компонент вектора х, может быть записана в следующем виде:

(1)

где w называется весовым вектором, а — величиной порога. В ос­нову линейного классификатора для двух классов положено сле­дующее решающее правило: принять решение , если g(x)>0, и , если g(x)<0. Таким образом, х приписывается к , если ска­лярное произведение w^tx превышает порог —. Если g(x)=0, то обычно х можно отнести к любому из классов, однако в данной главе это соответствие будет считаться неопределенным.

Уравнение g(x)=0 определяет поверхность решений, отделяю­щую точки, соответствующие решению , от точек, соответствую­щих решению . Когда функция g(x) линейна, данная поверхность представляется гиперплоскостью. Если и x₁, и x₂ принадлежат по­верхности решений, то справедливо следующее выражение:

или

,

так что w есть нормаль по отношению к любому вектору, лежащему в гиперплоскости. В общем случае гиперплоскость H делит про­странство признаков на два полупространства: область решений для и область решений для . Поскольку g(x)>0, если х находится в области , то из этого следует, что нормальный вектор w направлен в сторону . В этом случае иногда говорят, что любой вектор х, находящийся в области , лежит на положительной сто­роне гиперплоскости Н, а любой вектор х, находящийся в области , лежит на отрицательной стороне H.

Разделяющая функция g(x) представляет собой алгебраическое расстояние от х до гиперплоскости. Это становится более очевидным, если выразить х в следующем виде:

,

где Хр—нормальная проекция х на гиперплоскость H, а r — соот­ветствующее алгебраическое расстояние, положительное, если х находится с положительной стороны гиперплоскости, и отрица­

тельное, если х находится с отрицательной стороны гиперплоскос­ти. Тогда, поскольку g(x_p)=0,

или

В частности, расстояние от начала координат до гиперплоскости Н выражается отношением /||w||. Если <0, начало координат находится с положительной стороны Н; если <0,— с отрица­тельной стороны Н.

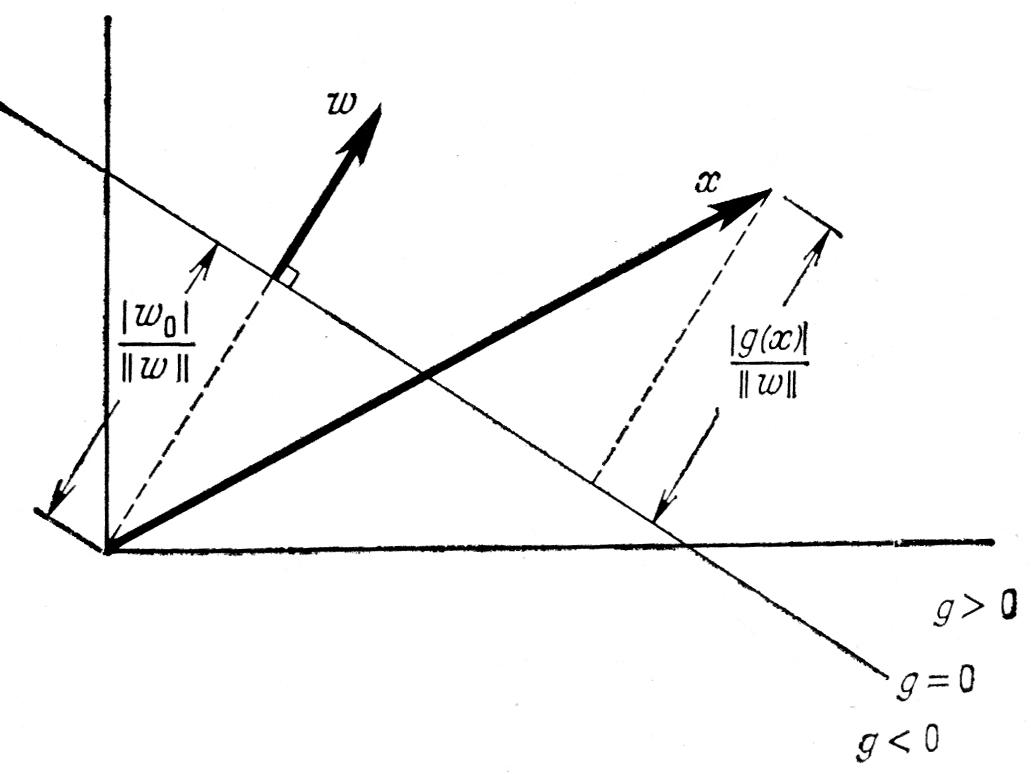
Рис. 5.1.Линейная граница областей решений

Если =0, то функция g(x) становится однородной w^tx, и гиперплоскость проходит через начало координат. Геометрическая интерпретация данных результатов приведена на рис. 5.1.

В заключение можно сделать вывод, что линейная разделяющая функция делит пространство признаков поверхностью решений, представляющей собой гиперплоскость. Способ ориентации данной поверхности задается нормальным вектором w, а положение ее — величиной порога . Разделяющая функция g(x) пропорциональ­на взятому со знаком расстоянию от х до гиперплоскости, при этом g(x)>0, когда х находится с положительной стороны гиперплос­кости, и g(x)<0, когда х находится с отрицательной стороны.