4.9. Аппроксимация для бинарного случая

4.9.1. Разложение Радемахера - Уолша

Когда составляющие вектора х дискретны, задача оценки плот­ности распределения становится задачей оценки вероятности Р(х=v_k). По идее задача эта еще проще, нужно только считать, сколько раз наблюдается х, чтобы получить значение v_k, и воспользоваться законом больших чисел. Однако рассмотрим случай, когда d сос­тавляющих вектора х бинарны (имеют значения 0 или 1). Поскольку имеется 2^d возможных векторов v_k, мы должны оценить 2^d вероят­ностей, что представляет собой огромную задачу при больших зна­чениях d, часто возникающих в работе по распознаванию образов.

Если составляющие вектора х статистически независимы, зада­ча намного упрощается. В этом случае можем написать

(40)

(41)

(42)

Таким образом, в этом частном случае оценка для Р(х) сводится к оценке d вероятностей p_i. Более того, если мы возьмем логарифм Р(х), то увидим, что он является линейной функцией от х, что уп­рощает как запоминание данных, так и вычисление:

(43)

где

(44)

Естественно поинтересоваться, существуют ли какие-либо ком­промиссные решения между полной строгостью, для достижения которой требуется оценка 2^d вероятностей, и вынужденным принятием статистической независимости, что сведет всю проблему к оцен­ке только d вероятностей. Разложение для Р(х) и аппроксимация Р(х) частичной суммой дают один ответ. Когда имеются бинарные переменные, естественно использовать полиномы Радемахера — Уолша в качестве базисных функций. Такое множество 2^d полино­мов можно получить путем систематического образования произве­дений различных сомножителей 2х_i—1, которые получаются сле­дующим образом: ни одного сомножителя, один сомножитель, два и т. д. Таким образом, имеем

(45)

Нетрудно заметить, что эти полиномы удовлетворяют отношению ортогональности

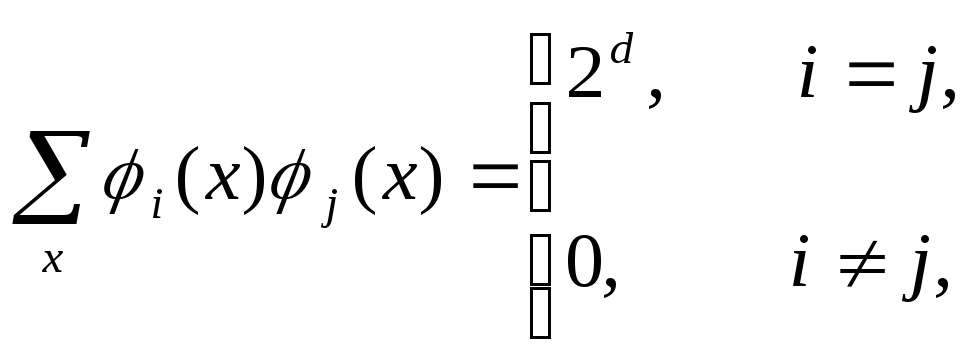(46)

где суммирование проводится по 2^d возможным значениям х. Итак, любую функцию Р(х), определенную на единичном d-кубе, можно разложить как

(47)

где

(48)

Рассматривая Р(х) как вероятностную функцию видим, что

(49)

Поскольку функции Радемахера — Уолша (х) — полиномы, видим, что коэффициенты , являются в сущности моментами. Так что, если Р(х) неизвестна, но имеется n выборок x₁, . . ., х_n коэффи­циенты можно оценить, вычисляя моменты выборок :

(50)

В пределе с устремлением п к бесконечности эта оценка по за­кону больших чисел должна сойтись (по вероятности) к истинному значению .

Теперь выражение (47) дает нам точное разложение для Р(х), и в этом случае оно не упрощает наши вычисления. Вместо оценки совместных вероятностей мы должны оценитьмоментов — ко­эффициентов . Можно, однако, аппроксимировать Р(x), усекая разложение и вычисляя только моменты низкого порядка. Аппрок­симация первого порядка, полученная с помощью первых 1+d членов, будет линейной относительно х. Аппроксимация второго порядка, содержащая первые 1+d+a(d—l)/2 членов, будет квад­ратичной относительно х ⁶. В целом выражение (47) показывает, что для аппроксимации полиномами Радемахера — Уолша степени k требуется оценка моментов порядка k и ниже. Эти моменты можно оценить, исходя из данных, или вычислить непосредственно из Р(х). В последнем случае тот факт, что можно суммировать сначала по переменным, не включенным в полином, говорит о том, что нужно знать только вероятности каждой переменной порядка k. Например, разложение первого порядка определяется вероятностями р_i=P(x_i= l):

где

Естественно поинтересоваться, насколько хорошо такое усечен­ное разложение аппроксимирует действительную вероятность Р(х). В общем, если мы аппроксимируем Р (х) с помощью рядов, включаю­щих подмножество полиномов Радемахера — Уолша,

то можно использовать отношения ортогональности, чтобы показать, что сумма квадратичной ошибки (Р(х) — (х))² минимизируется выбором =. Таким образом, усеченное разложение является оптимальным в смысле среднеквадратичной ошибки. Кроме того, коль скоро в аппроксимацию входит постоянный полином , можно легко показать, что(х)=1, что и требуется. Однако ничто не может предотвратить превращение(х) в отрицательную величину для некоторого х. Действительно, еслине входит в полином, то(х)=0 и по крайней мере одна из вероятностей должна быть отри­цательной. Этого досадного результата можно избежать путем раз­ложенияlog Р (х), а не Р (х), хотя в этом случае мы уже не сможем больше быть уверены в том, что суммирование полученной аппрок­симации для Р (х) даст единицу.