4.10. Линейный дискриминант Фишера

Одной из непреходящих проблем, с которой сталкиваются при применении статистических методов для распознавания образов, является то, что Беллманом было названо проклятием размерности. Процедуры, выполнимые аналитически или непосредственным вы­числением в пространствах небольшой размерности, могут стать совершенно неприменимыми в пространстве с 50 или 100 измерения­ми. Были разработаны различные методы уменьшения размерности пространства признаков в надежде получить задачу, поддающуюся решению.

Можно уменьшить размерность с d измерений до одного, просто проецируя d-мерные данные на прямую. Конечно, особенно если выборки образуют хорошо разделенные компактные группы в d-пространстве, проекция на произвольную прямую обычно смешивает выборки из всех классов. Однако, вращая эту прямую, мы можем найти такую ориентацию, для которой спроецированные выборки будут хорошо разделены. Именно это является целью классического дискриминантного анализа.

Предположим, что мы имеем множество п d-мерных выборок x₁, . . ., х_n, n₁ в подмножестве , помеченном и n₂ в подмно­жестве , помеченном . Если мы образуем линейную комбина­цию компонент вектора х, получим скалярную величину

(66)

и соответствующее множество п выборок y₁, . . ., y_n разделенное на подмножества и . Геометрически, если ||w||=l, каждая компонента , есть проекция соответствующего на прямую в на­правленииw. В действительности величина w не имеет реального значения, поскольку она просто определяет масштаб у. Однако направление w имеет значение. Если мы вообразим, что выборки, помеченные , попадают более или менее в одну группу, а выборки, помеченные , попадают в другую, то мы хотим, чтобы проекции на прямой были хорошо разделены и не очень перемешаны. На рис. 4.6 показан выбор двух различных значений w для двумерного случая.

Мерой разделения спроецированных точек служит разность сред­них значений выборки. Если есть

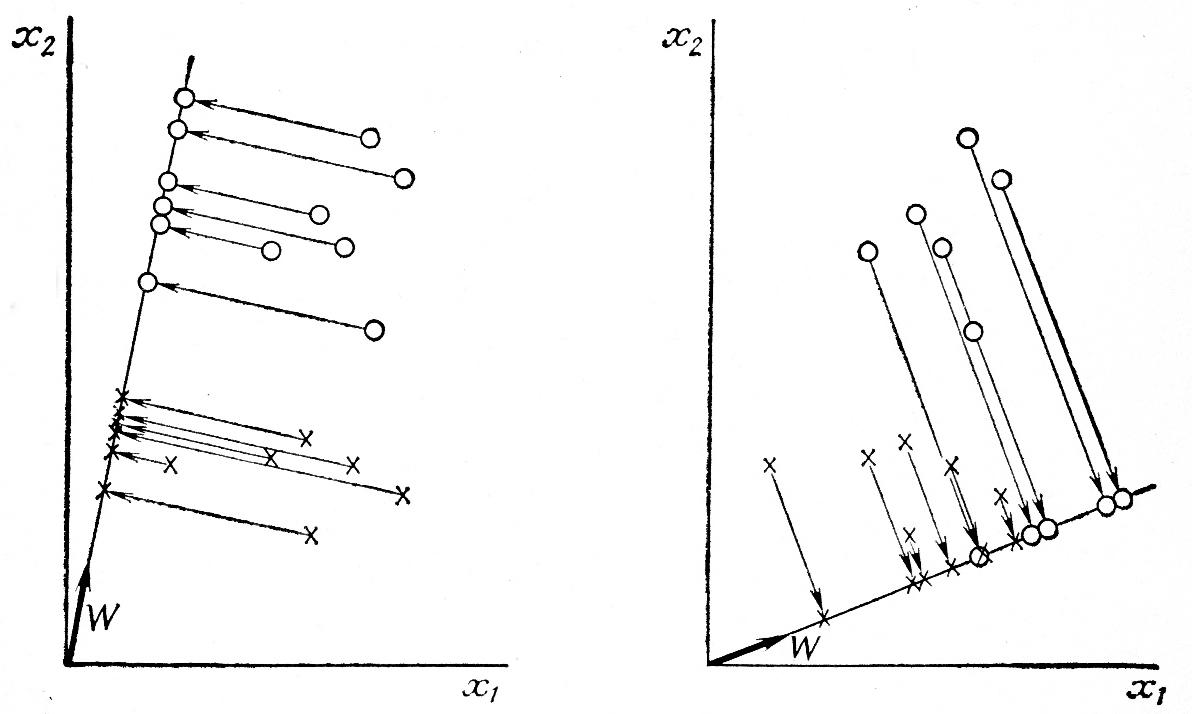
Рис. 4.6. Проекция выборок на прямую.

среднее значение d-мерной выборки, заданное как

(67)

то среднее значение выборки для спроецированных точек задается посредством

(68)

Отсюда следует, что |-|=|w^t(—)| и что мы можем сделать эту разность сколь угодно большой, просто масштабируя w. Конечно, чтобы получить хорошее разделение спроецированных данных, мы хотим, чтобы разность между средними значениями была велика относительно некоторого показателя стандартных отклоне­ний для каждого класса. Вместо получения дисперсий выборок оп­ределим разброс для спроецированных выборок, помеченных , посредством

. (69)

Таким образом, (l/n)(+ ) является оценкой дисперсии сово­купности данных, a + называется полным разбросом внутри класса спроецированных выборок. Линейный дискриминант Фишера тогда определяется как такая линейная разделяющая функция ⁷ w^tx, для которой функция критерия

(70)

максимальна.

Чтобы получить J как явную функцию от w, определим матрицы разброса S_i и S_w посредством

(71)

и

S_W =S₁+S₂ (72)

Тогда

(73)

так что

+ =(74)

Аналогично

(-)= (75)

где

= . (76)

Матрица называется матрицей разброса внутри класса. Она пропорциональна ковариационной выборочной матрице для совокупности d-мерных данных. Она будет симметричной, положи­тельно полуопределенной и, как правило, невырожденной, если n>d. называется матрицей разброса между классами. Она также симметричная и положительно полуопределенная, но из-за того, что она является внешним произведением двух векторов, ее ранг будет самое большее единица. В частности, для любого w направление w совпадает с направлением — и — вполне вырожденная матрица.

При помощи и функцию критерия J можно представить в виде

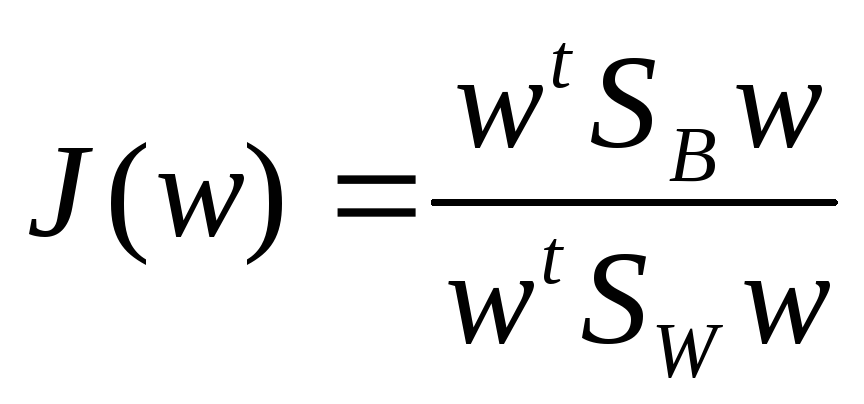(77)

Это выражение хорошо известно в математической физике как обобщенное частное Релея. Легко показать, что вектор w, который максимизирует J, должен удовлетворять соотношению

(78)

что является обобщенной задачей определения собственного значе­ния. Если является невырожденной, мы можем получить обыч­ную задачу определения собственного значения, написав

(79)

В нашем частном случае не нужно находить собственные значе­ния и собственные векторы из-за того, что направление w всегда совпадает с направлением —. Поскольку масштабный множитель для w несуществен, мы можем сразу написать решение

(80)

Таким образом, мы получили линейный дискриминант Фишера — линейную функцию с максимальным отношением разброса между классами к разбросу внутри класса. Задача была преобразована из d-мерной в более приемлемую одномерную. Это отображение п-мерного множества на одномерное, и теоретически оно не может уменьшить минимально достижимый уровень ошибки. В общем мы охотно жертвуем некоторыми теоретически достижимыми результа­тами ради преимущества работы в одномерном пространстве. Когда же условные плотности распределения p(x|) являются многомер­ными нормальными с равными ковариационными матрицами , то даже не нужно ничем жертвовать. В этом случае мы вспоминаем, что граница оптимальных решений удовлетворяет уравнению

w^tx+=0

где

и  есть константа, включающая в себя w и априорные вероятности. Если мы используем средние значения и ковариационную матрицу выборок для оценки и , то получаем вектор в том же направле­нии, что и w, удовлетворяющий (80), который максимизирует J.

Таким образом, для нормального случая с равными ковариациями оптимальным решающим правилом будет просто решение , если линейный дискриминант Фишера превышает некоторое пороговое значение, и решение — в противном случае.