4.3. Парзеновские окна

4.3.1. Общие соображения

Знакомство с методом оценки плотностей распределения с по­мощью парзеновского окна можно начать с временного предполо­жения о том, что область _n является d-мерным гиперкубом. Если h_n есть длина ребра этого гиперкуба, то его объем задается как

(6)

Аналитическое выражение для k_n— количества выборок, попа­дающих в этот гиперкуб,— можем получить, определяя следующую функцию окна:

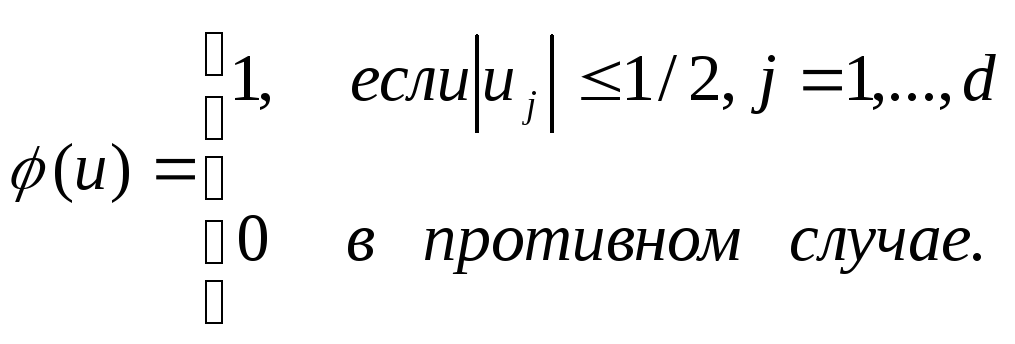
Таким образом, u определяет единичный гиперкуб с центром в начале координат. Отсюда следует, что ((x-x_i)/h_n) равняется единице, если х_i находится в гиперкубе объема V_n с центром в х, или нулю в любом другом случае. Следовательно, количестве выборок в этом гиперкубе задается выражением

Подставляя его в (5), получаем оценку

. (8)

Это соотношение предполагает более общий подход к оценке плот­ности распределения. Не ограничиваясь функцией окна гиперкуба, данной формулой (7), допускаем более общий класс функций окна. Тогда соотношение (8) выражает нашу оценку р(х) как среднее зна­чение функций от х и выборок х_i. По существу, функция окна ис­пользуется для интерполяции, причем каждая выборка влияет на оценку в зависимости от ее расстояния до х.

Хотелось бы, чтобы оценка р_n(х) была законной плотностью рас­пределения, т. е. неотрицательной, с интегралом, равным единице. Это можно гарантировать, требуя, чтобы функция окна была законной плотностью распределения. Точнее, если мы потребуем, чтобы

(u)0 (9)

и

(10)

и если мы сохраняем отношение V_n=,то отсюда сразу же следует что и p_n(х) также удовлетворяет этим условиям.

Рассмотрим, какое влияние оказывает на p_n(х) ширина окна h_n. Если мы определяем функцию (х) как

(11)

то можем записать p_n(х) в виде среднего

(12)

Поскольку V_n=, то h_n влияет как на амплитуду, так и на ширину окна (х). Еслиh_n очень велика, то амплитуда у мала, их должно находиться достаточно далеко от х_i, пока (х— х_i) не станет значительно отличаться от (0). В этом случае p_n(х) есть наложение п широких, медленно меняющихся функций и служит очень сглаженной «несфокусированной» оценкой p(х). С другой стороны, если h_n очень мала, то максимальное значение (х— х_i) велико и находится вблизи от х= х_i. В этом случае p_n(х) есть нало­жение п резких выбросов с центрами в выборках и является ошибоч­ной «зашумленной» оценкой функции р(х). Для любого значения h_n справедливо выражение

. (13)

Таким образом, по мере устремления h_n к нулю (х— х_i) стремится к дельта-функции Дирака, центрированной в х_i и p_n(х) стремится к наложению дельта-функций, центрированных в выборках.

Ясно, что выбор значения h_n (или V_n) сильно сказывается на p_n(х). Если объем V_n слишком велик, оценка будет плохой из-за слишком малой разрешающей способности. Если V_n слишком мал, оценка будет плохой в результате слишком большого статистиче­ского разброса. При ограниченном количестве выборок самое луч­шее решение — пойти на приемлемый компромисс. При неограни­ченном же количестве выборок можно позволить V_n медленно стре­миться к нулю по мере увеличения п и заставить p_n() сойтись к не­известной плотности распределения р(х).

Говоря о сходимости, мы должны сознавать, что речь идет о сходимости последовательности случайных величин, так как для любого фиксированного х значение p_n (х) зависит от значений слу­

чайных выборок x₁, . . ., х_n. Таким образом, p_n(х) имеет некоторое среднее и некоторую дисперсию(х). Будем говорить, что оценкаp_n(х) сходится к р(х), если ²

(14)

и

(15)

Чтобы доказать сходимость, нужно наложить условия на неиз­вестную плотность распределения р(х), функцию окна (u) и ширину окна h_n. Обычно требуется, чтобы р была непрерывной в х и чтобы выполнялись условия (9) и (10). Можно доказать, что сходимость обеспечивается при следующих дополнительных условиях:

, (16)

, (17)

(18)

(19)

Выражения (16) и (17) способствуют хорошему поведению , и этим условиям удовлетворяет большинство плотностей распреде­ления, которые можно взять для функций окна. Уравнения (18) и (19) говорят о том, что объем V_n должен стремиться к нулю, но со скоростью, меньшей чем 1/п. Рассмотрим теперь, почему эти усло­вия—основные условия, обеспечивающие сходимость.