4.4. Оценка методом kn ближайших соседей

Одна из проблем, с которой сталкиваются при использовании ме­тода парзеновского окна, заключается в выборе последовательности объемов ячеек V₁, V₂, . . . . Например, если мы берем V_n,=V₁/, то результаты для любого конечного п будут очень чувствительны к выбору начального объема V₁. Если V₁ слишком мал, большинство объемов будут пустыми и оценка р_n(х) будет довольно ошибочной. С другой стороны, если V₁ слишком велик, то из-за усреднения по объему ячейки могут быть потеряны важные пространственные от­клонения от р(x). Кроме того, вполне может случиться, что объем ячейки, уместный для одного значения х, может совершенно не годиться для других случаев.

Один из возможных способов решения этой проблемы - сделать объем ячейки функцией данных, а не количества выборок. Напри­мер, чтобы оценить р (х) на основании n выборок, можно центриро­вать ячейку вокруг х и позволить ей расти до тех пор, пока она не вместит выборок, где есть некая определенная функция от п. Эти выборки будут ближайшими соседями х. Если плотность рас­пределения вблизи х высокая, то ячейка будет относительно неболь­шой, что приводит к хорошему разрешению. Если плотность рас­пределения невысокая, то ячейка возрастает, но рост приостанав­ливается вскоре после ее вступления в области более высокой

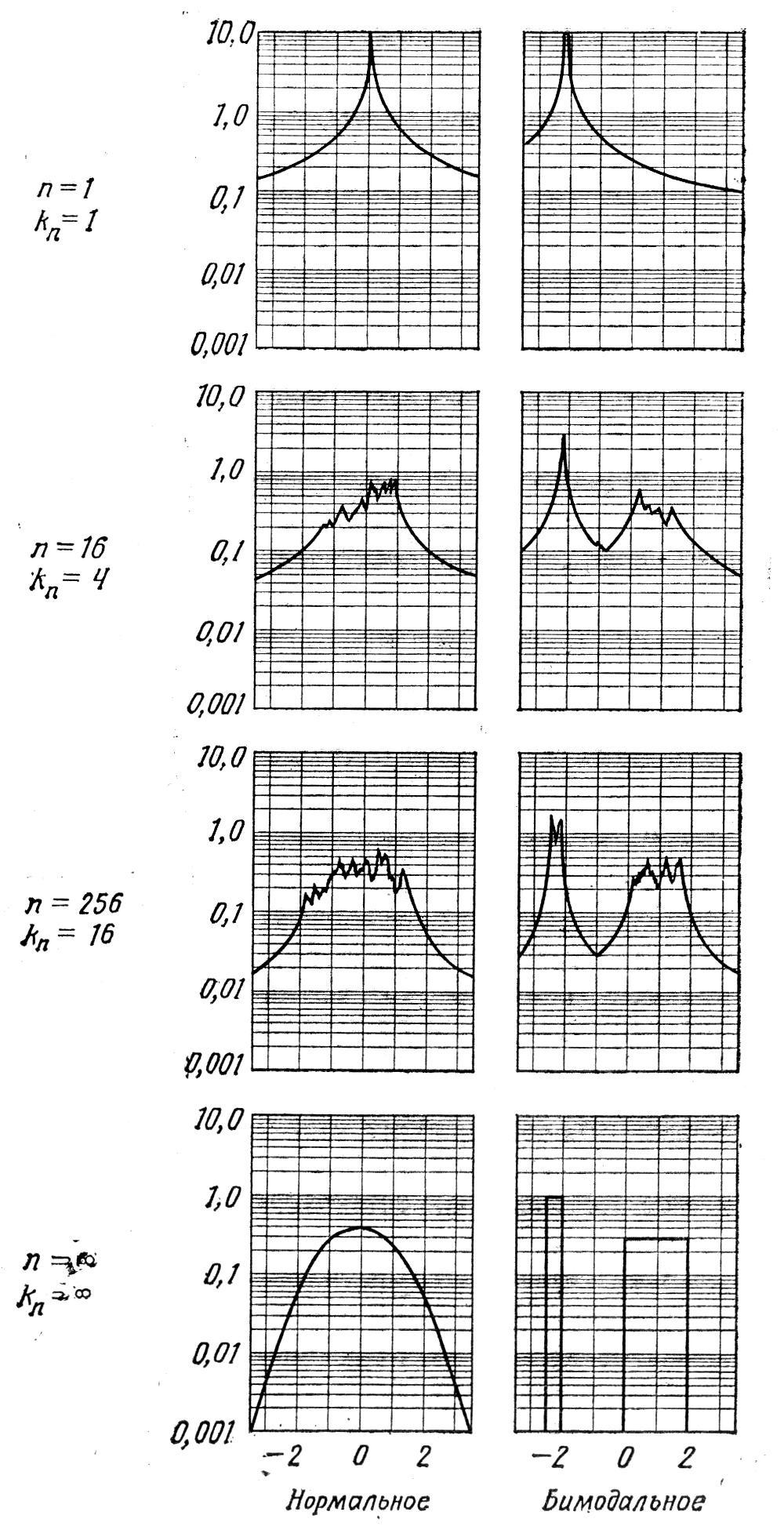
Рис. 4. 3. Оценки двух плотностей распределения, полученные методом k_n бли­жайших соседей.

плотности распределения. В любом случае, если мы берем

(5)

мы хотим, чтобы стремилось к бесконечности при стремлении п к бесконечности, так как это гарантирует, что /n будет хорошей оценкой вероятности попадания точки в ячейку объема Однако мы хотим также, чтобы росло достаточно медленно для того, чтобы размер ячейки, необходимый для вмещения выборок, сжал­ся до нуля. Таким образом, из формулы (5) видно, что отношение /n должно стремиться к нулю. Хотя мы не приводим доказательств, можно показать, что условия и являются необходимыми и достаточными для сходимости р_n (х) и р (х) по вероят­ности во всех точках, где плотность р непрерывна. Если взять k_n= и допустить, что р_n(х) является хорошей аппроксимацией р(x), то из соотношения (5) следует, что . Таким образом, опять имеет вид , но начальный объем опре­деляется характером данных, а не каким-либо нашим произволь­ным выбором.

Полезно сравнить этот метод с методом парзеновского окна на тех же данных, что были использованы в предыдущих примерах. С n=l и == 1 оценка становится

Ясно, что это плохая оценка для р (х), поскольку ее интеграл рас­ходится. Как показано на рис. 4.3, оценка становится значительна лучше по мере увеличения n несмотря на то, что интеграл оценки всегда остается бесконечным. Этот неприятный факт компенсиру­ется тем, что р_n(х) никогда не сведется к нулю просто потому, что в некоторую произвольную ячейку или окно не попадают никакие выборки. Хотя эта компенсация может показаться скудной, в про­странствах более высокой размерности она приобретает большую ценность.

Как и в методе парзеновского окна, мы можем получить семей­ство оценок, принимая = и выбирая различные значения для . Однако при отсутствии какой-либо дополнительной инфор­мации любой выбор одинаково хорош, и мы можем быть уверены лишь в том, что результаты будут асимптотически правильными.