4.6.2. Сходимость при использовании метода ближайшего соседа

Теперь мы хотим оценить среднюю вероятность ошибки для правила ближайшего соседа. В частности, если Р_n(е) есть уровень ошибки с п выборками и если

(27)

то мы хотим показать, что

Р*РР*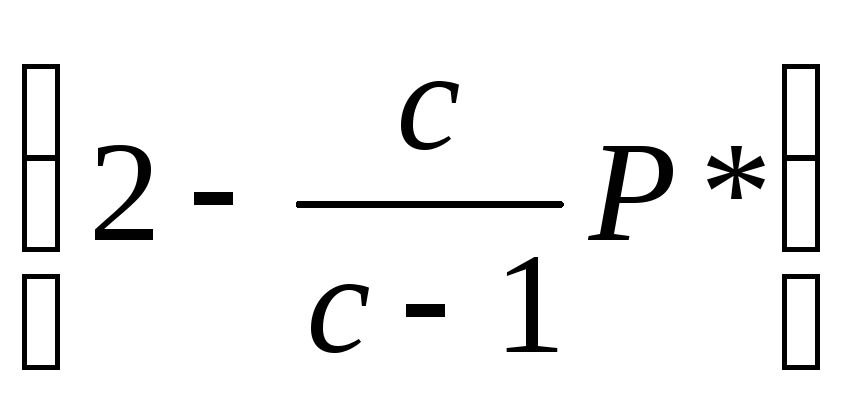. (28)

Начнем с замечания, что при использовании правила ближайшего соседа с конкретным множеством п выборок результирующий уро­вень ошибки будет зависеть от случайных характеристик выборок. В частности, если для классификации х используются различные множества п выборок, то для ближайшего соседа вектора х будут получены различные векторы . Так как решающее правило зависит от ближайшего соседа, мы имеем условную вероятность ошибки, которая зависит как от х, так и от . Усредняя по , получаем

(29)

Обычно очень трудно получить точное выражение для условной плотности распределения p(|х). Однако, поскольку, по опре­делению является ближайшим соседом х, мы ожидаем, что эта плот­ность будет очень большой в непосредственной близости от х и очень малой во всех других случаях. Более того, мы ожидаем, что по мере устремленияп к бесконечности р(|х) будет стремиться к дельта-функции с центром в х, что делает оценку, задаваемую (29), тривиальной. Для того чтобы показать, что это действительно так, мы должны допустить, что плотность р для заданного х непрерывна и не равна нулю. При таких условиях вероятность попадания любой выборки в гиперсферу S с центром в х есть некое положительное число

Таким образом, вероятность попадания всех n независимо взя­тых выборок за пределы этой гиперсферы будет (1—P_S)ⁿ, стремя­щейся к нулю по мере устремления п к бесконечности. Итак, сходится к х по вероятности ир (| х) приближается к дельта-функ­ции, как и ожидалось. Вообще говоря, применяя методы теории меры, можно получить более убедительные (и более строгие) доказа­тельства сходимостик х, но для наших целей достаточно получен­ного результата.

4.6.3. Уровень ошибки для правила ближайшего соседа

Обратимся теперь к вычислению условной вероятности ошибки Р_n(е|х, ). Чтобы избежать недоразумений, необходимо поставить задачу более тщательно, чем это делалось до сих пор. Когда мы гово­рим, что у нас имеетсяп независимо сделанных помеченных выбо­рок, то мы имеем в виду n пар случайных переменных (x₁, ), (x₂, ), . . ., (х_n , ), где может быть любым изс состояний природы , . . . , . Мы полагаем, что эти пары получались путем выбора состояния природы для с вероятностьюP(), а затем путем выбора х_i в соответствии с вероятностным законом p(х|), причем каждая пара выбирается независимо. Положим теперь, что природа выбирает пару (х,) и что , помеченноеесть ближайшая к х выборка. Поскольку состояние природы при выборене зависит от состояния при выборе х, то

(30)

Теперь, если применяется решающее правило ближайшего со­седа, мы совершаем ошибку всякий раз, когда =. Таким образом, условная вероятность ошибки Р_n(е|х, ) задается в виде

(31)

Чтобы получить Р_n(е), надо подставить это выражение в (29) вместо Р_n(e|х), а затем усреднить результат по х. Вообще это очень трудно сделать, но, как мы уже замечали ранее, интегрирование в (29) становится тривиальным по мере устремления n к бесконечности, а р(, х) к дельта-функции. ЕслиР(, х) непрерывна в х, получаем

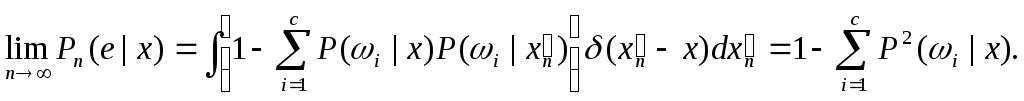(32)

Так что асимптотический уровень ошибки правила ближайшего соседа, если можно поменять местами интегрирование и переход

к пределу ⁴, задается выражением

(33)