1.3. Вычисление
Постановка задачи. Вычислить предел
где
f(n)
—
бесконечно
большая последовательность порядка па
и g(п)
—
бесконечно
большая последовательность порядка
п
В
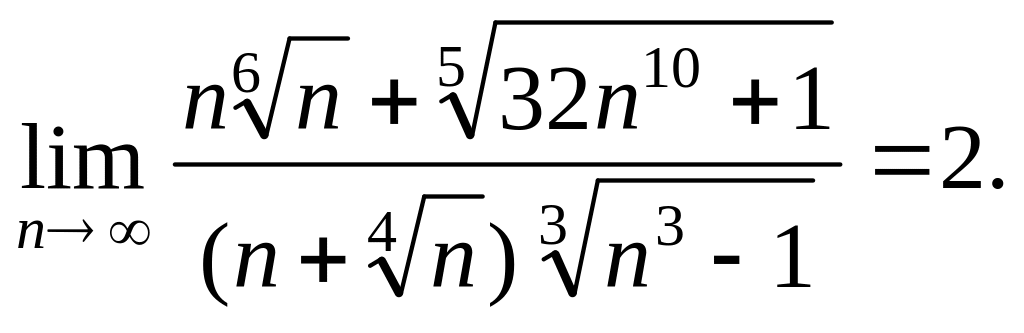ынесем
в знаменателе множитель
,
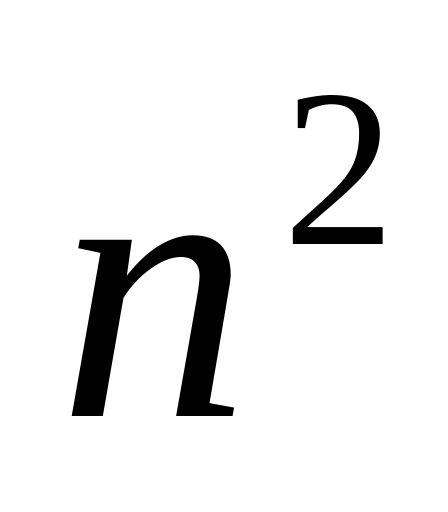получим
2. Вынесем в знаменателе множитель n2, получим
3. Имеем
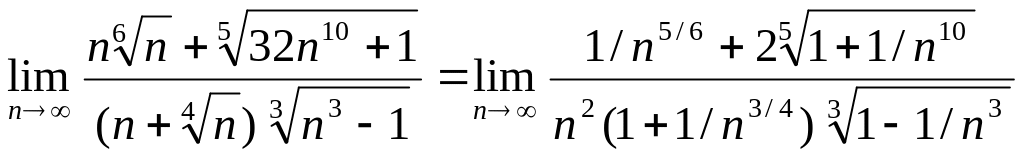
4. Сокращая n2 и используя теоремы о пределах, окончательно получаем
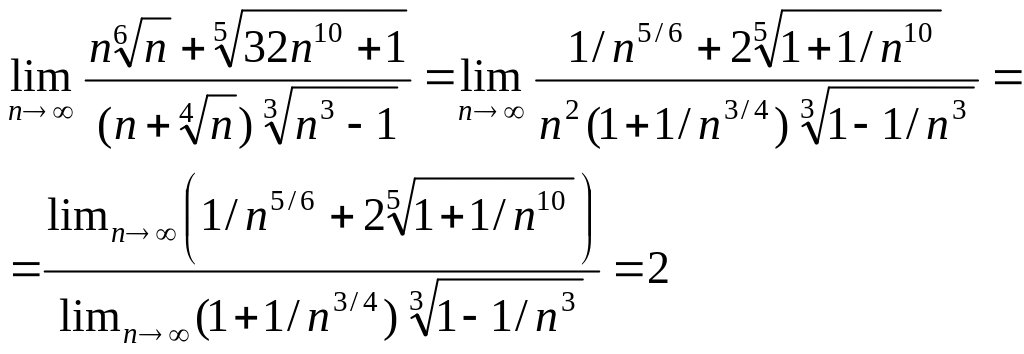
З
амечание.
В данном случае было использовано
свойство корня, в
силу которого
и
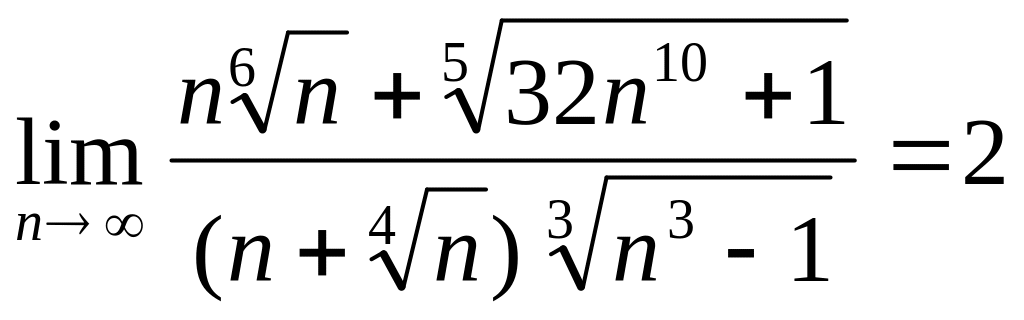
Ответ,
Задания для самостоятельной работы
Условия задач. Вычислить пределы.
1
. 2.
3. 4.
5. 6.
7
. 8.
9. 10.
Ответы.
1.
.
2.0. 3. +
.
4.3. 5.0. 6. -3. 7. -1. 8. +
.
9.5. 10. -2.
1.4. Вычисление
Постановка задачи. Вычислить предел последовательности
где
План решения.
1. Преобразуем выражение под знаком предела так, чтобы использовать второй замечательный предел, т.е. выделим единицу:
где
a(n)
= u(n)
—
1 — бесконечно малая последовательность
при
.
Так
как а(п)
0 при n
, то
Если
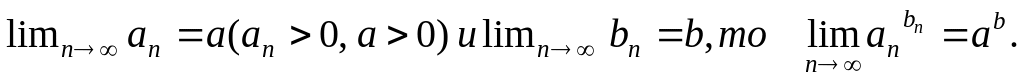
Следовательно, если существует предел
то окончательно имеем
Пример. Вычислить предел
Решение.
1. При выражение под знаком предела представляет собой степень, основание которой стремится к единице:
а
показатель — к минус бесконечности:
Преобразуем выражение под знаком предела так, чтобы использовать второй замечательный предел:
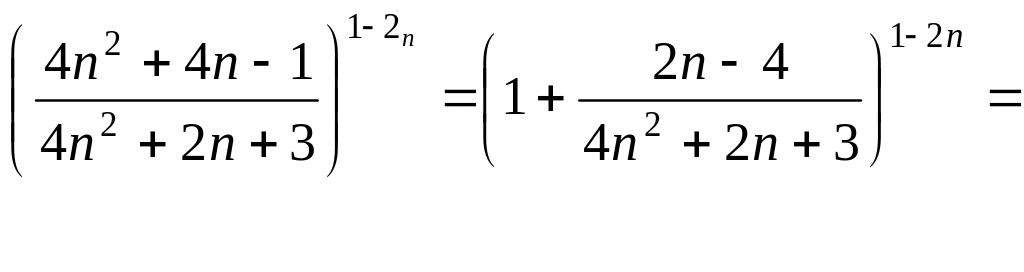
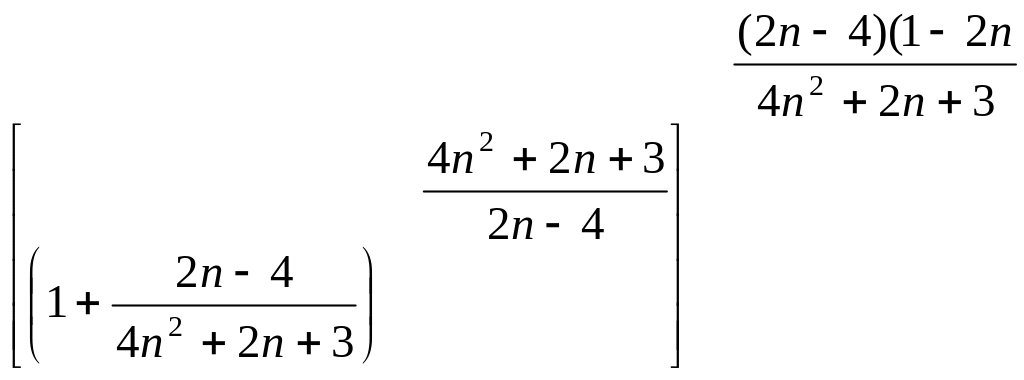
Так как
при
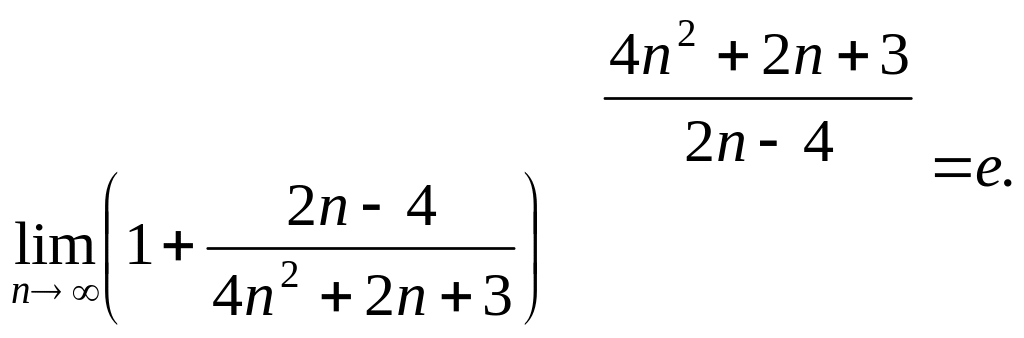
2. Так как
то окончательно имеем
Ответ
Задания для самостоятельной работы
Условия задач. Вычислить пределы.
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
9.
|
8.
10.
|
Ответы.
1. е3. 2.
3. е. 4. е. 5. е-2. 6. е2. 7. 1. 8. е6. 9.
е-5. 10. +
.
1.5. Понятие предела функции
Постановка задачи. Пользуясь определением предела функции в точке, доказать, что
План решения.
1. Число А называется пределом функции f(х) в точке х — а, если
Это
значит, что
неравенство
имеет
решение
2. Для того чтобы найти S(e), сначала найдем множество М такое, что
,
т.е.
решим неравенство.
Затем найдем <5(е) такое, что
Тогда будем иметь
Это означает, что
Записываем ответ в виде:
Пример. Доказать, что
Решение.
Число 8 называется пределом функции
в точке
,
если
Для того чтобы найти
,
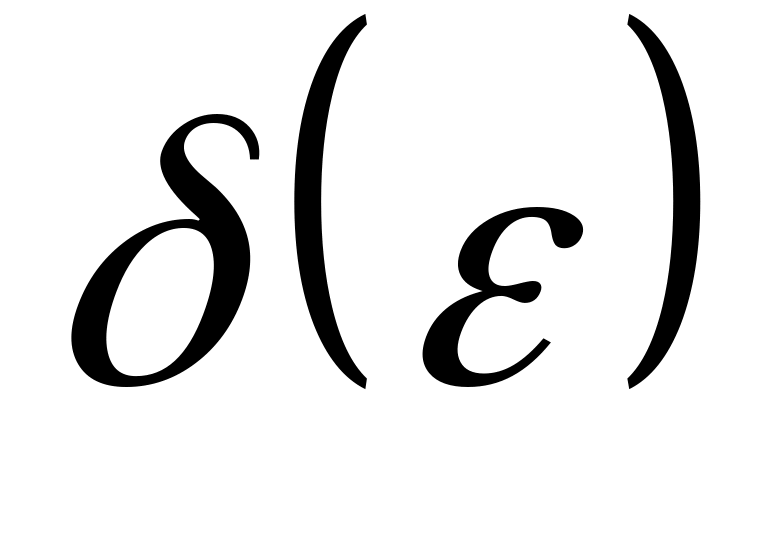сначала найдем множество М такое что
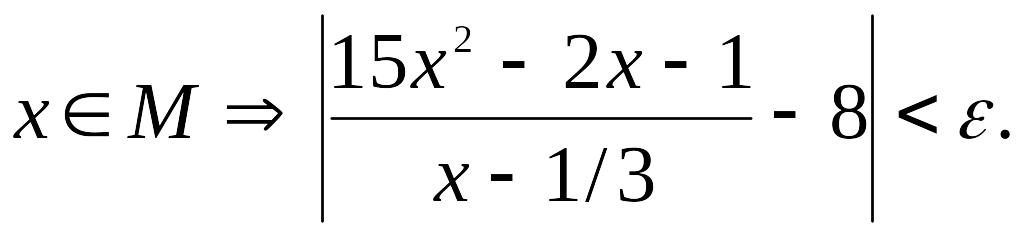
т.е. решим неравенство
Затем найдем
такое, что
Тогда будем иметь
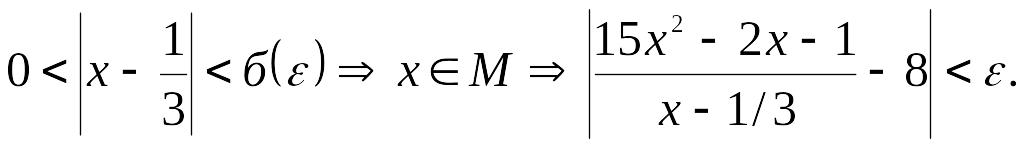
Решаем неравенство:
(так как в определении
предела функции в точке
,
т.е.
,
то можно сократить дробь на множитель
.
Таким образом,
Следовательно, если
то
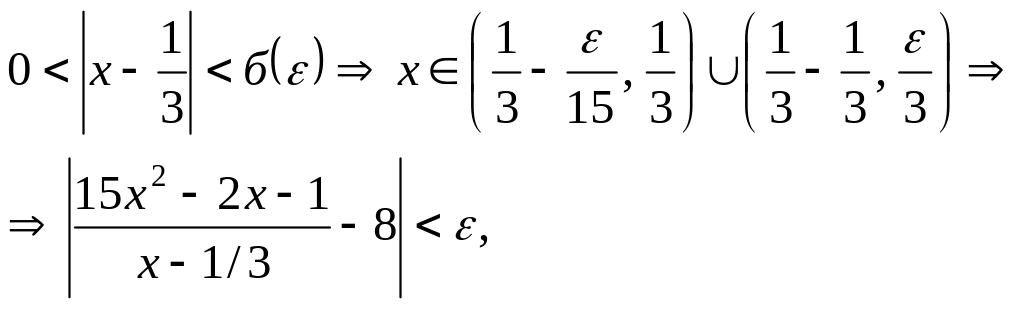
т.е.
Ответ.
Задания для самостоятельной работы
Условия задач. Пользуясь определением пределе функции в точке, доказать равенства.
1.
|
2.
|
3. |
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
Ответы.
