§2. Нахождение изображения по оригиналу

Изображение оригинала можно найти с помощью таблицы оригиналов и изображений, а также используя свойства преобразования Лапласа.

Таблица 1

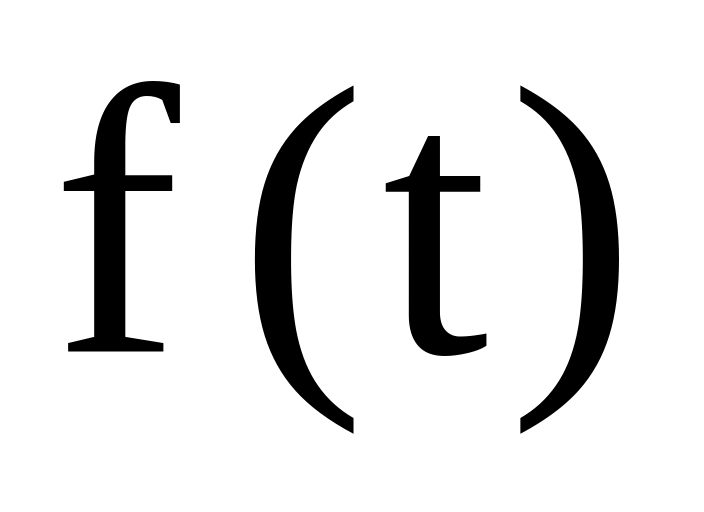
№	Оригинал	Изображение
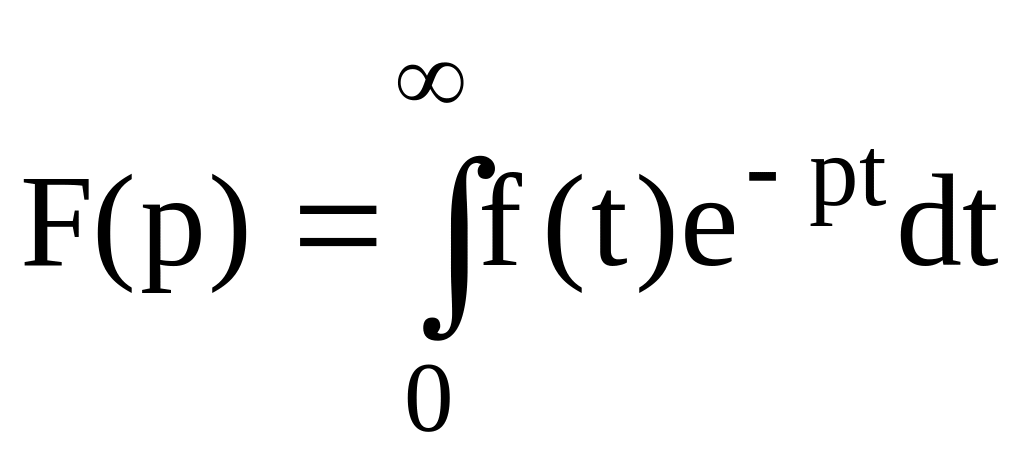
1	1
2
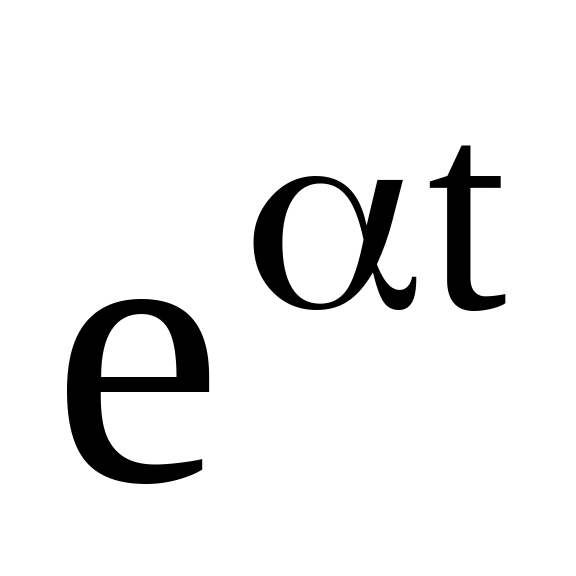
3	t
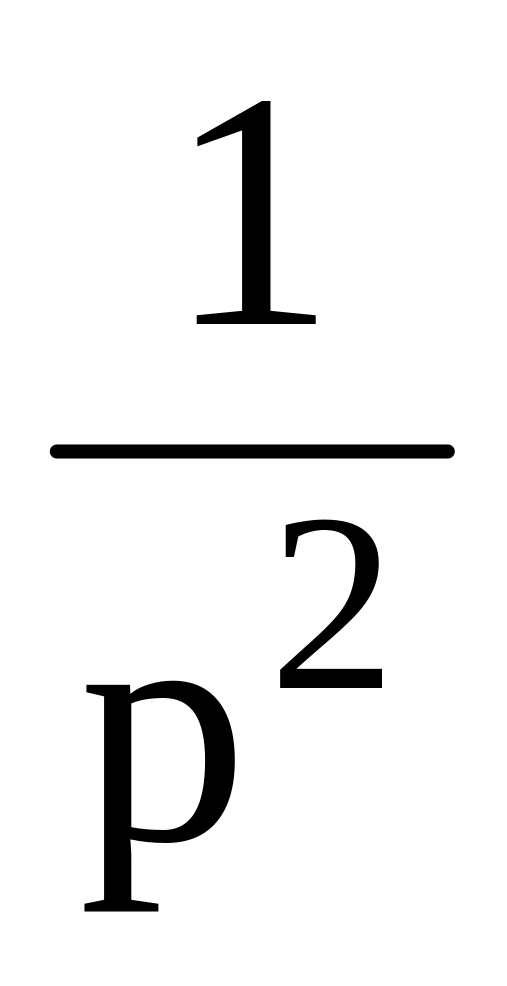
4
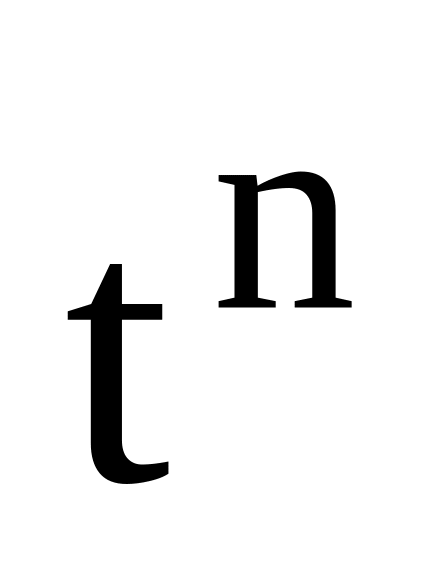
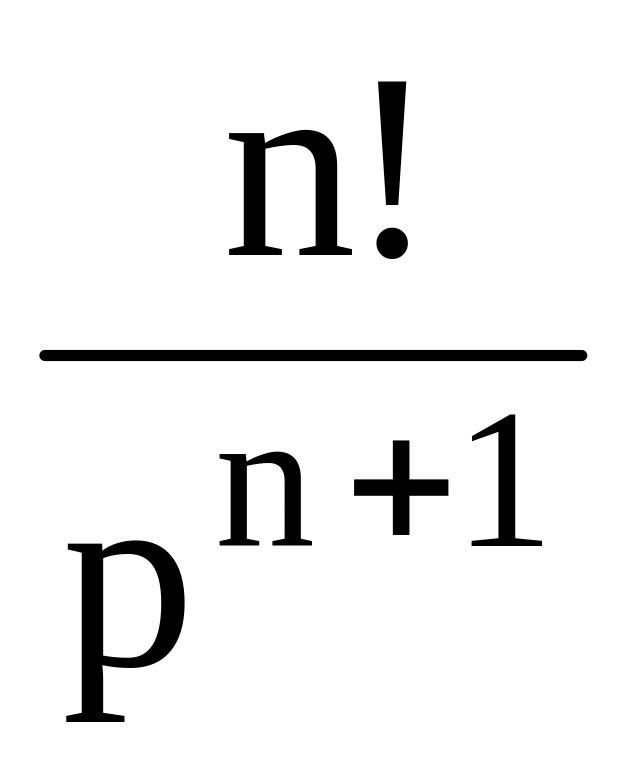
5
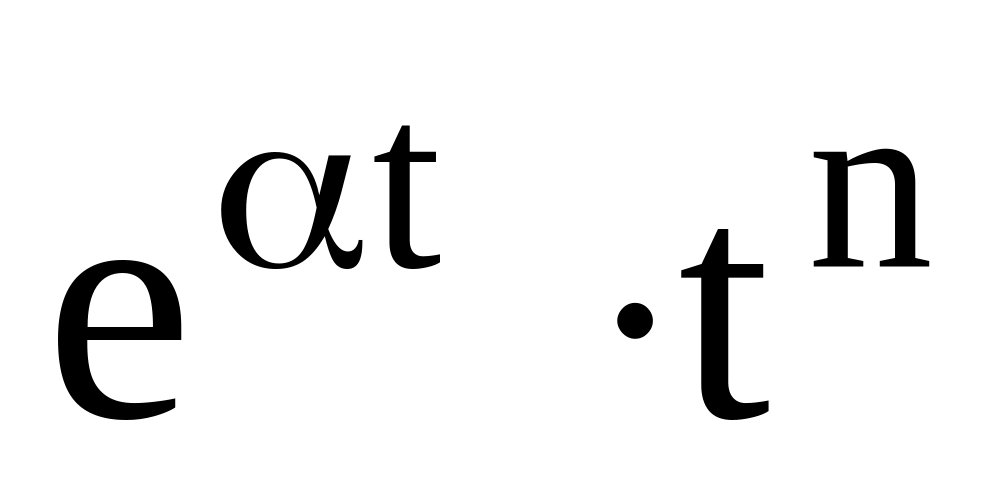
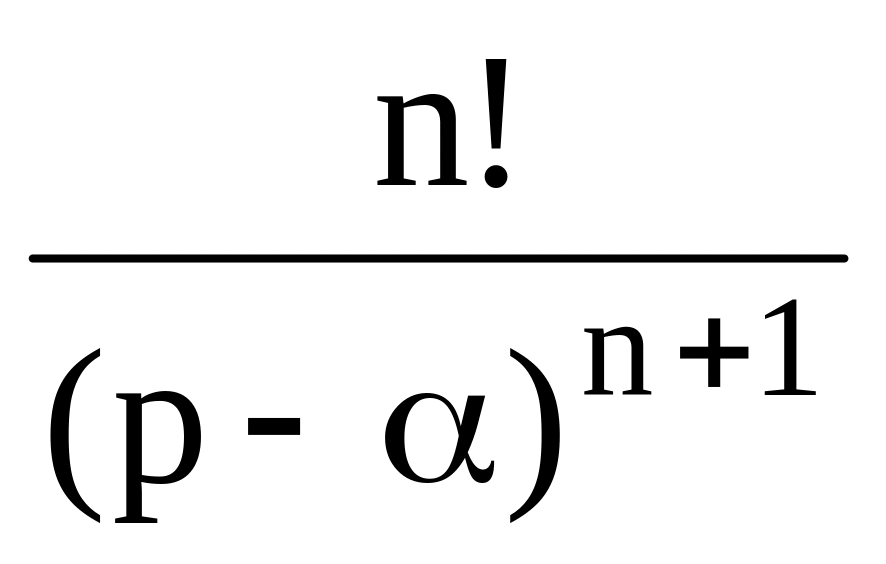
6
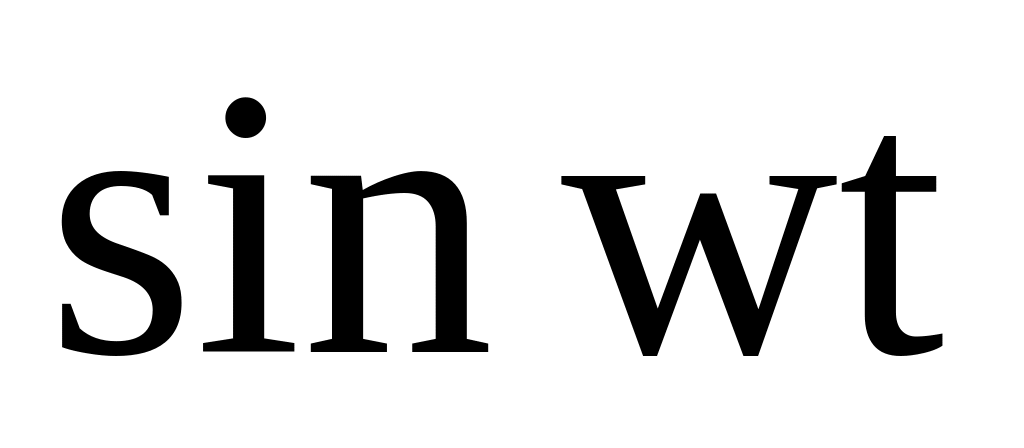
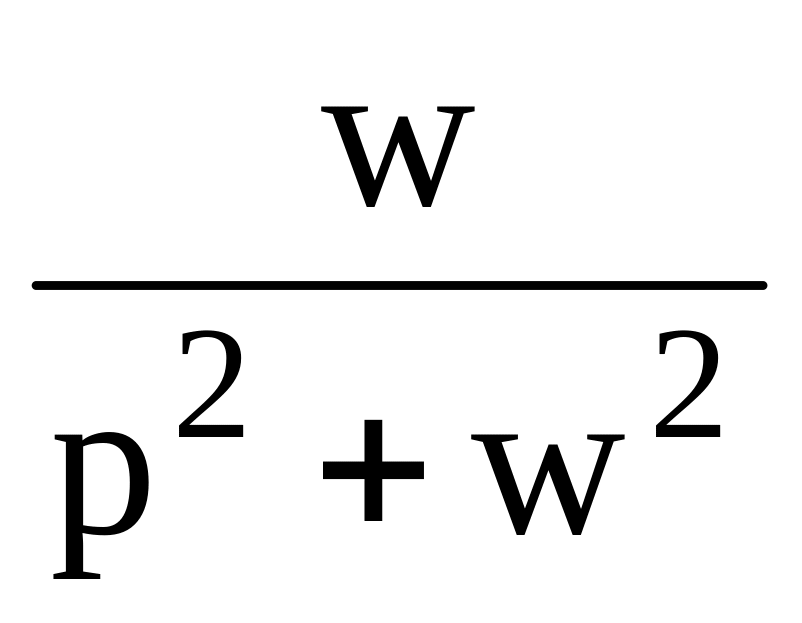
7
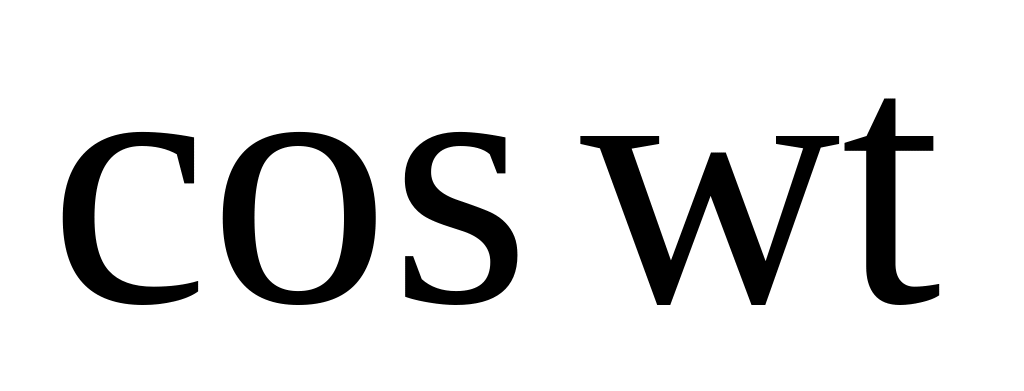
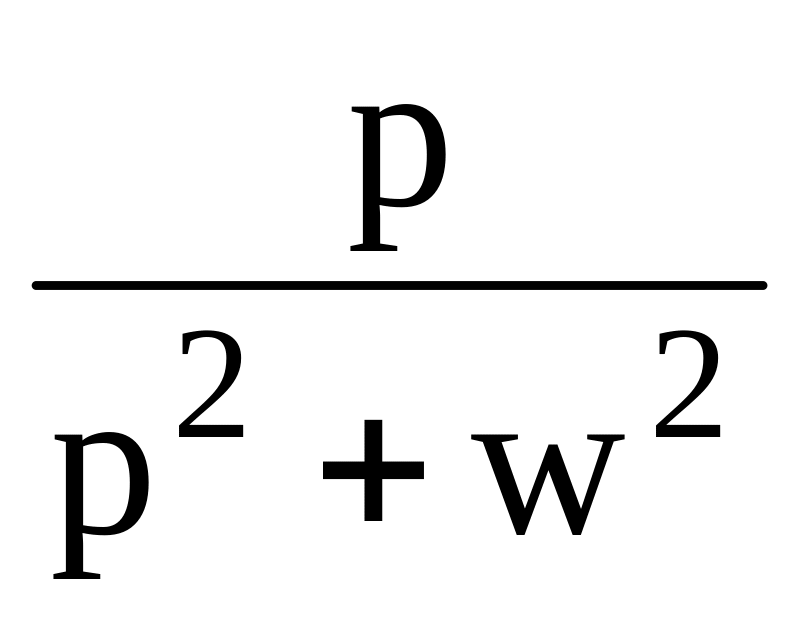
8
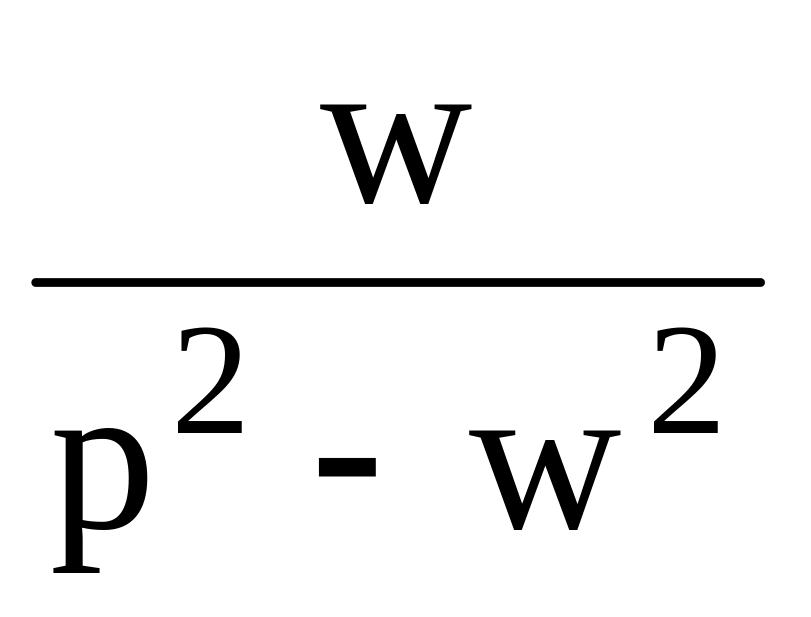
9
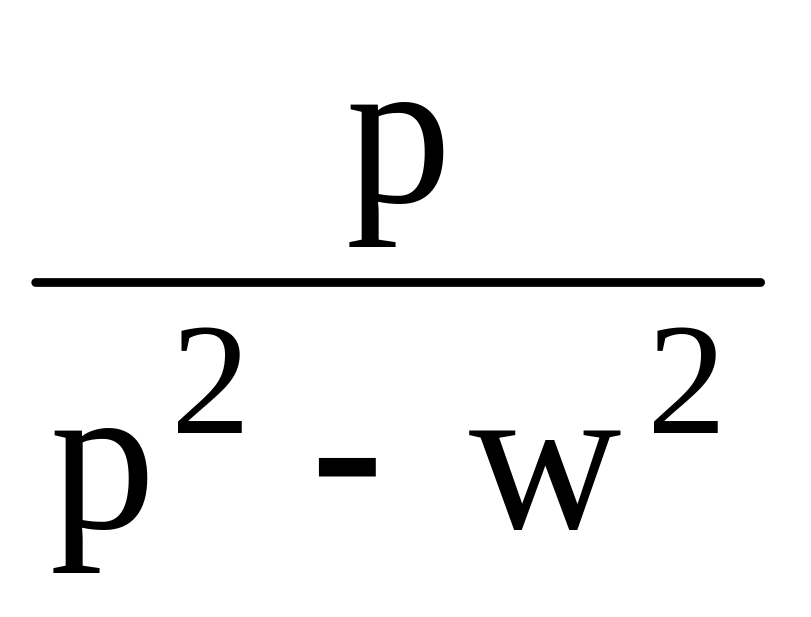
10
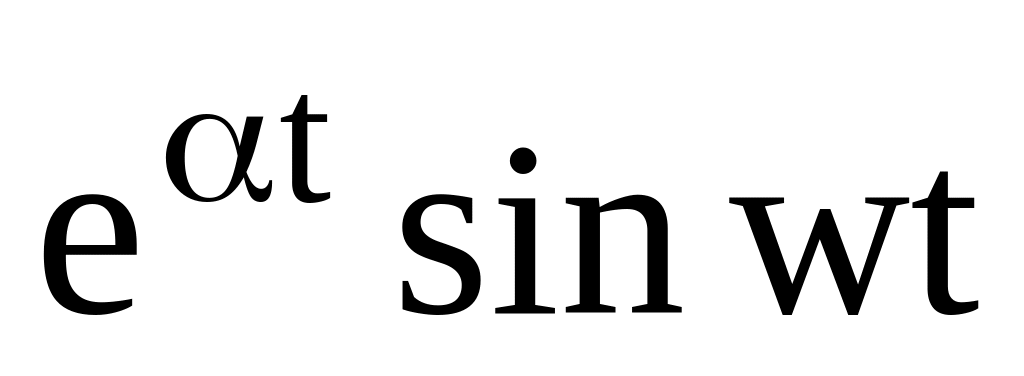
11
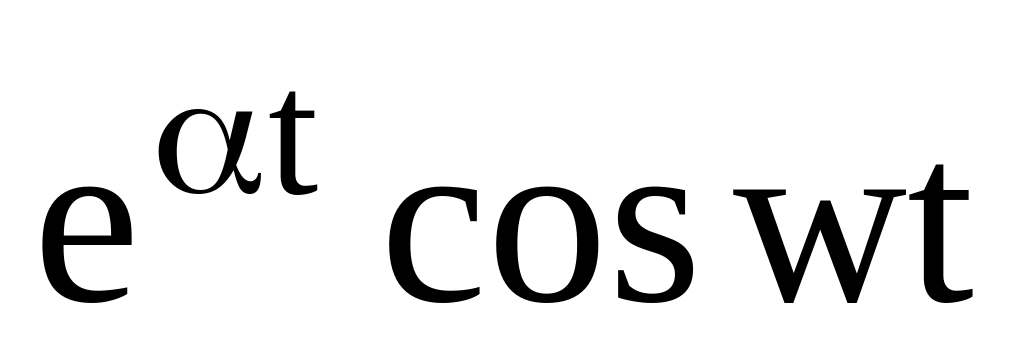
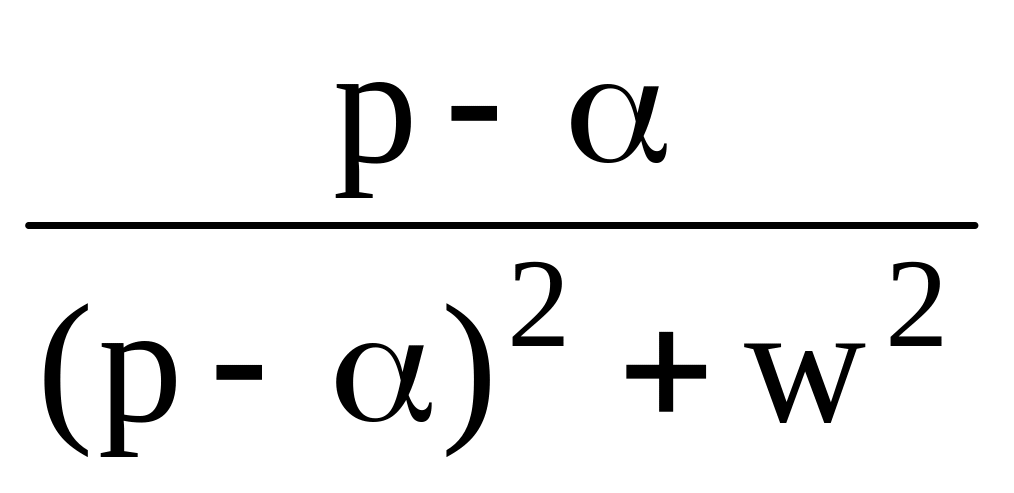
12
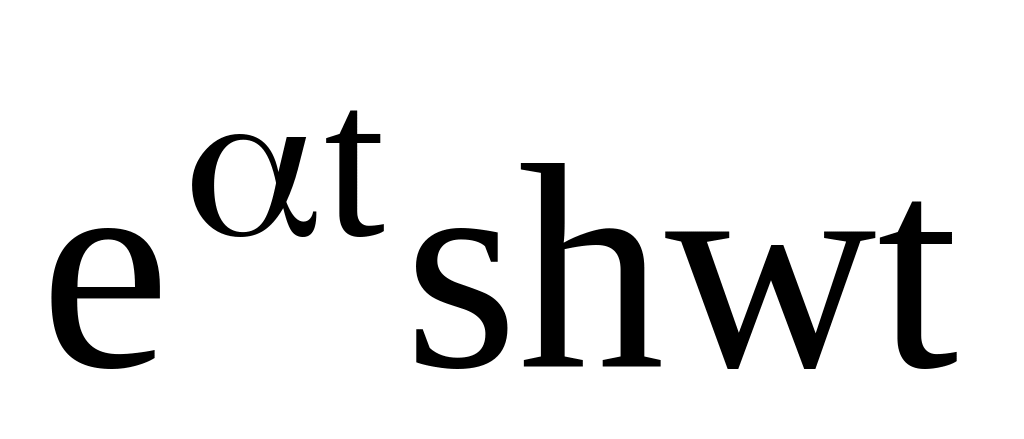
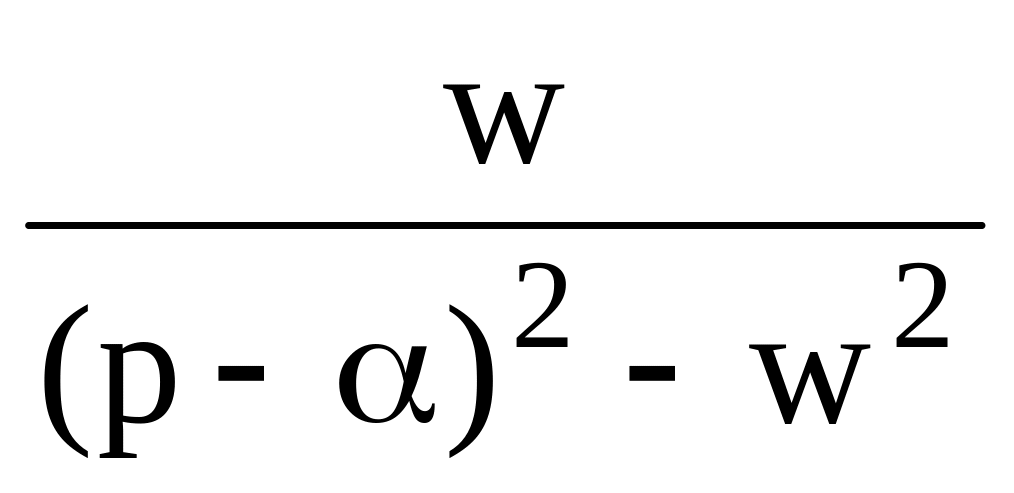
13
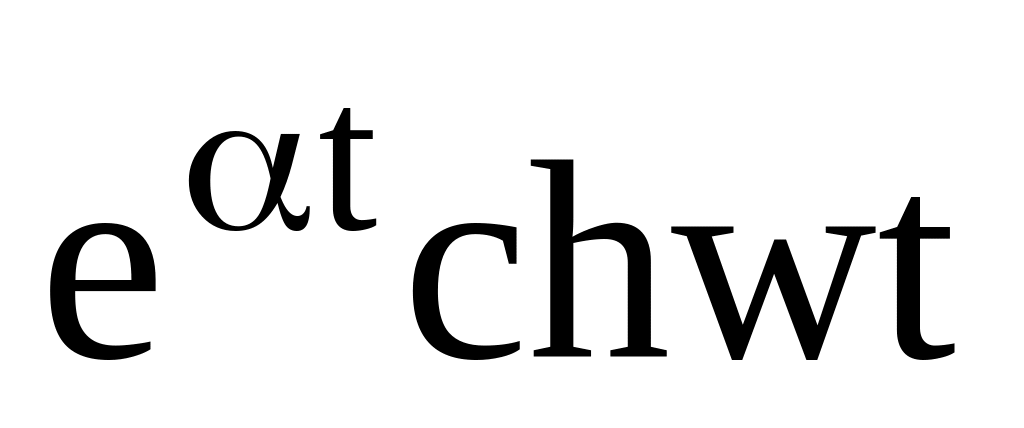
14
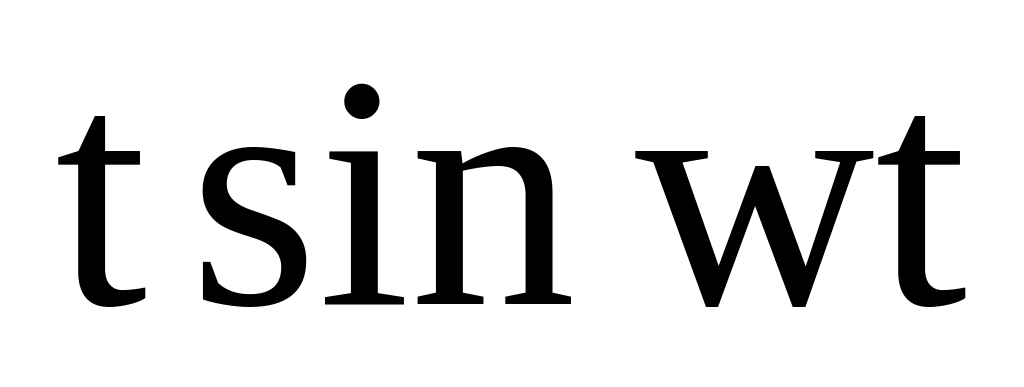
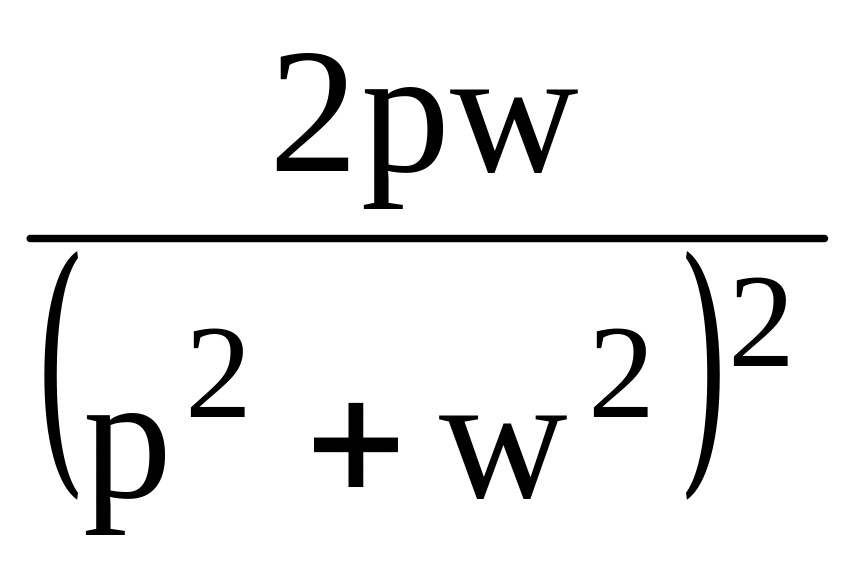
15
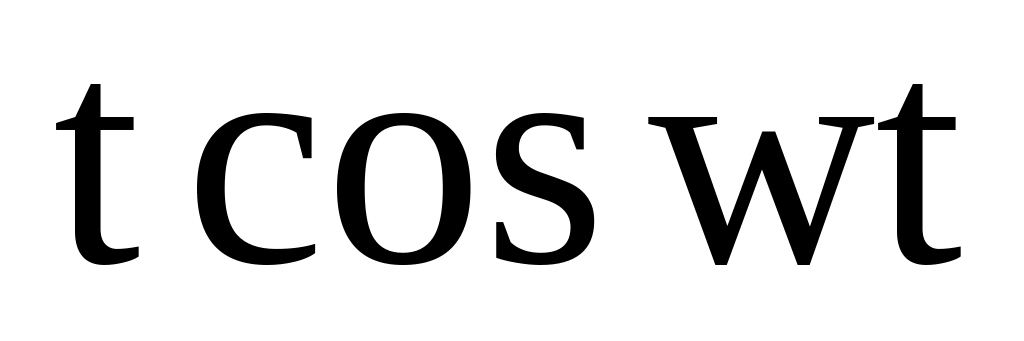
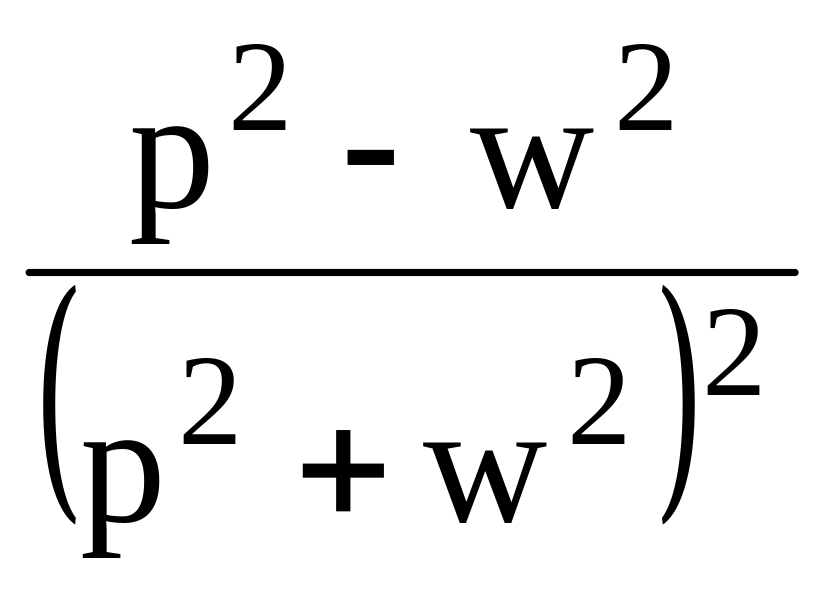
16
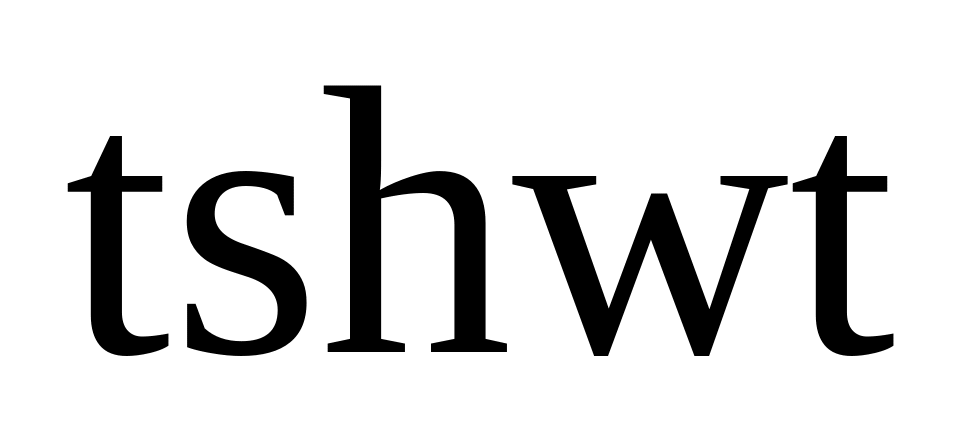
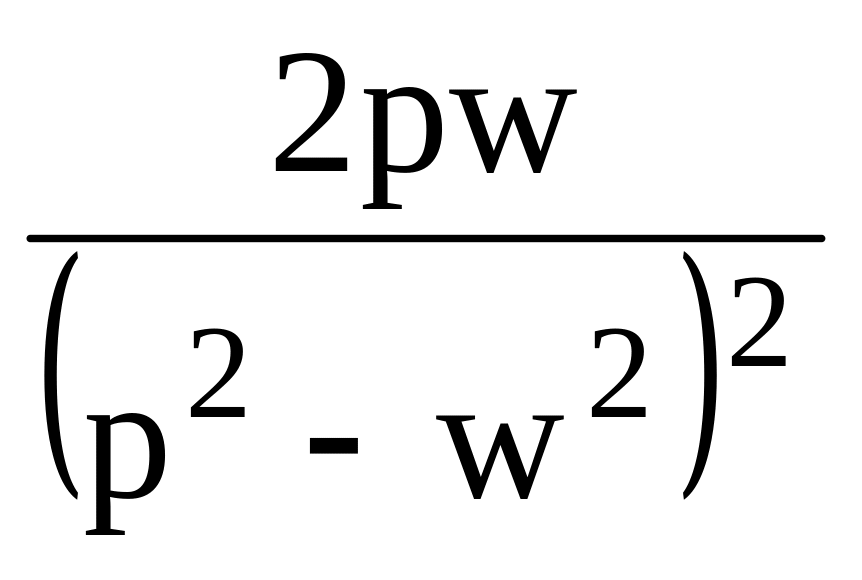
17
18
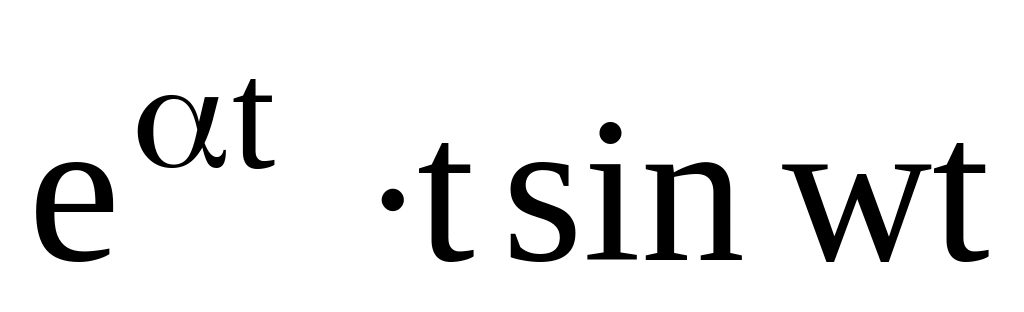
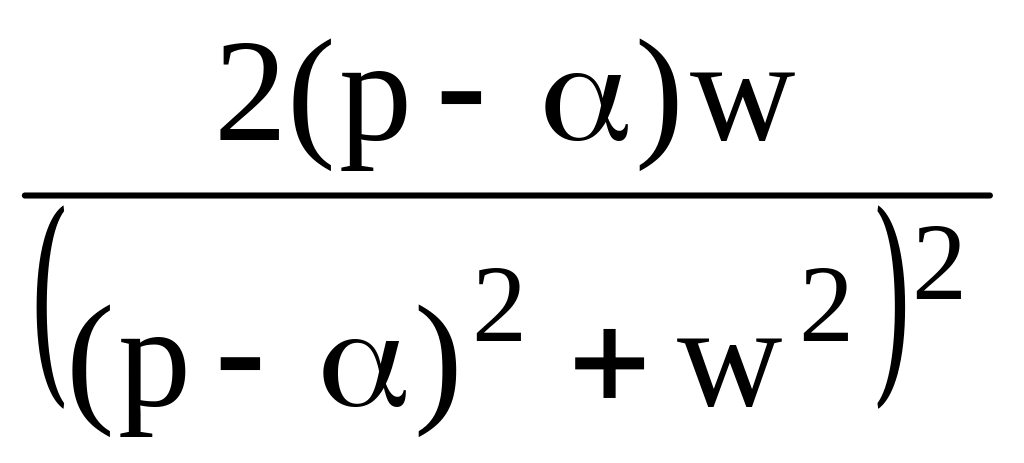
19

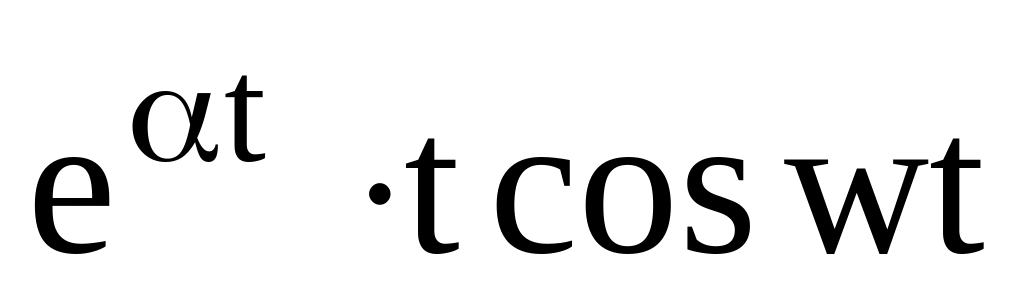
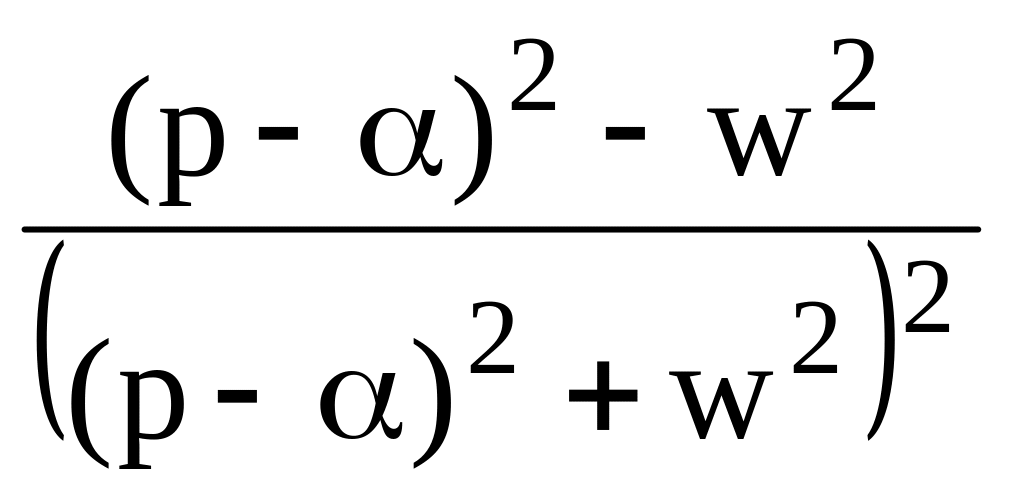
Найти изображения по оригиналам:

97). а) б)

в) г)

98). а) б) в)

г) ; д) .

§3. Нахождение оригинала по изображению

Оригинал по изображению находиться с помощью обратного преобразования Лапласа по формуле обращения.

.

Здесь а – действительное число и , где – показатель роста оригинала f(t).

Правило 1. Если изображение – простейшая дробь III типа ( ), то необходимо в знаменателе дроби выделить полный квадрат, затем представить эту дробь в виде суммы двух дробей, выполнив почленное деление, и оригиналы полученных слагаемых найти по таблице 1.

Правило 2. Если разложение знаменателя дроби содержит множителем квадратный трехчлен и , то эту дробь можно методом неопределенных коэффициентов разложить на сумму простейших дробей, найти их оригиналы и полученные оригиналы сложить.

Теорема 1. (Первая теорема разложения). Если изображение F(p) представлено рядом Лорана, те при всех p, для которых , то соответствующий оригинал является суммой степенного ряда , сходящегося при всех

Теорема 2. (Вторая теорема разложения). Если изображение есть правильная несократимая рациональная дробь , знаменатель которой имеет m различных действительных корней соответственно кратности , то оригинал этого изображения есть функция

.

Следствие: Если изображение есть правильная несократимая рациональная дробь, знаменатель которой имеет только простые корни , то оригинал определяется по формуле

.

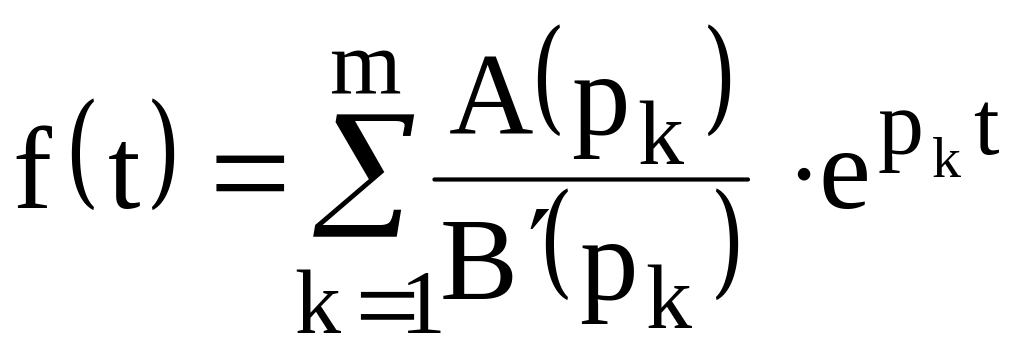Найти оригиналы по изображениям:

99). а) ; б) ; в) ;

100). а) б) ;

в) г)

101). а) б)

102). а) б)

103). а) ; б) ;