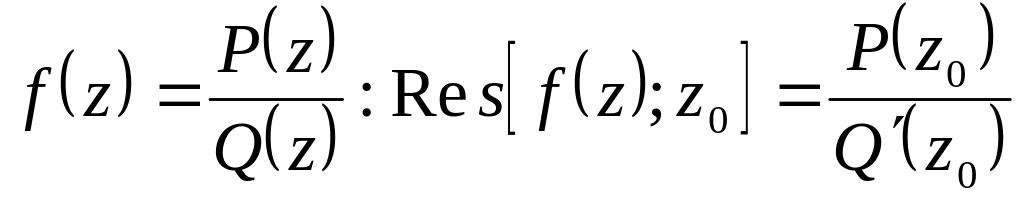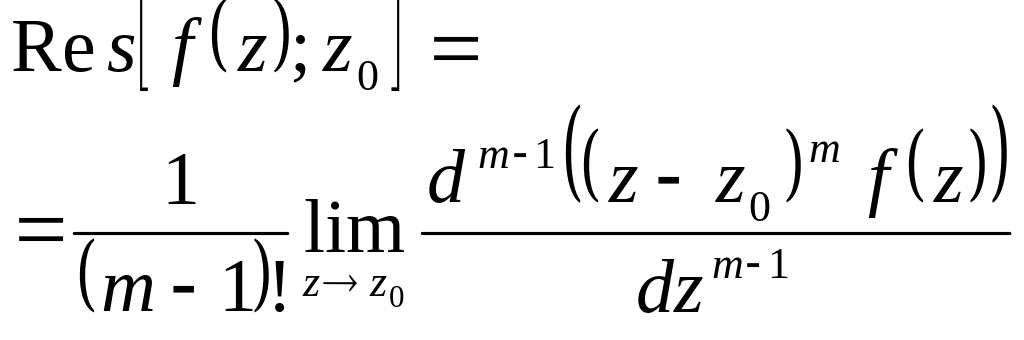Iy. Интеграл от функции комплексного переменного

IY.1. Определение Предел последовательности этих сумм при , если он существует, не зависит ни от способа разбиения кривой на дуги, ни от выбора точек t_k, называется интегралом от функции w = f(z) по кривой L и обозначается

.

Контурный интеграл – это комплексное число.

0. Правило вычисления контурного интеграла:

1. Выделяем в подинтегральной функции действительную и мнимую части, т. е. представляем в виде f(z) = u(x,y) + i v(x,y);

2. Запишем dz = dx + i dy;

3. Составляем произведение f(z) на dz

f(z)dz = (u + iv)(dx +idy) = (udx – vdy) +i(vdx+udy;

4. Вычисляем интеграл вдоль L

Замечания:

1. Если кривая L – есть окружность или часть ее - уравнение этой окружности и функция f(z) непрерывна в каждой точке L, то переменная интегрирования z записывается в показательной форме:

z = R e^iφ; dz = Re^iφidφ

2. Если x = x(t), y = y(t),где - параметрические уравнения кривей L, то z = x(t) + iy(t) называют комплексно – параметрическим уравнением кривой L; формула (1) преобразуется в формулу

41). Найти: где L – ломаная ;

42). Найти:

43). Найти где L – отрезок FB :

44). Найти , от т. до т. +1

45). Найти:

Iy.2. Формула Ньютона –Лейбница

,

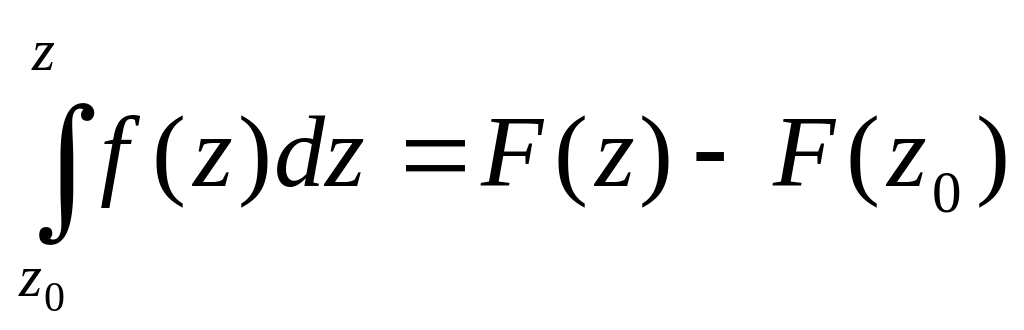где f(z) – аналитическая функция в области D, а z и z₀ есть соответственно начальная и конечная точка пути интегрирования L.

44). 45). , 46). ,

47). , 48). .

Iy.3. Теорема Коши для односвязной области

Если функция w = f ( z) - аналитическая в односвязной области D и на ее границе L, то, интеграл от f ( z) по L равен нулю:

.

Если область многозначна, то справедливо равенство

- где L₀ – внешний контур; здесь все контуры обходятся в одном направлении и функция аналитична между этими контурами

Iy.4. Интегральная формула Коши

Пусть w = f(z) аналитична в области D и на ее границе L . Тогда для каждой точки имеет место формула

. При этом функция имеет всюду в производные любого порядка, для которых справедливы формулы

Из этих формул можно выразить интегралы:

- интеграл Коши

Следствие:

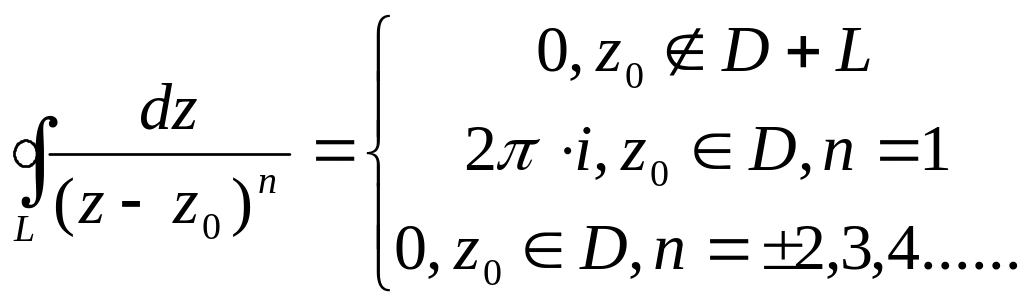
Вычислить следующие интегралы, пользуясь теоремой Коши, интегральной формулой Коши и формулами, полученными из интегральной формулы Коши дифференцированием. Направление вдоль контура в этих задачах – против часовой стрелки.

49). , где - окружность: а) ; б) .

50). , где .

51). , где а) ; б) .

52). , где а) ; б) .

53). , где .

54). , где .

55). , где а) : б) .

56). , где а) ; б) .

57). , где а) ; б) .

58). , где а) ; б) .

Y. Особые точки. Вычеты.

Y.1. Особые точки.

Точка называется особой точкой функции , если функция не аналитична в этой точке; и правильной, если в ней функция аналитична.

Особая точка функции называется изолированной, если в окрестности этой точки функция не имеет других особых точек

Если - изолированная особая точка функции , то в достаточно малом круге с выколотым центром функция будет аналитической и,следовательно, разлагается в ряд Лорана:

.

Изолированные особые точки бывают трех типов:

1) устранимые; 2) полюсы; 3) существенно особые точки.

Тип особых точек определяется либо по количеству членов в главной части ряда Лорана, либо по поведению функции в окрестности особой точки (см. таблицу 1).

Y.2. Вычеты

Определение: Вычетом функции относительно точки называется число, определяемое равенством:

или ,

где любой замкнутый контур, содержащий ; аналитическая на и в области, ограниченной , за исключением точки ; - первый коэффициент главной части ряда Лорана для функции в окрестности точки .

Формулы для вычетов относительно особых точек даны в таблице 1.

Таблица 1: Классификация особых точек и нахождение вычетов.

№	Особые точки	Ряд Лорана с главной частью	Поведение в точке	Формулы для нахождения вычетов
1.	Устранимая	Нет главной части.
2.	Простой полюс	В главной части одно слагаемое:		1) 2)
3.	Полюс кратности	В главной части слагаемых: .
4.	Существенно - особая	В главной части бесконечно много слагаемых	Не вуществует ( неопределен - – ность)	Разложить в ряд Лорана,

Теоремы о вычетах.

Теорема 1. Если функция аналитична в области , за исключением изолированных особых точек , лежащих в этой области, то для любого простого замкнутого контура , охватывающего точки , .

Теорема 2. Если аналитическая во всей комплексной плоскости, за исключением изолированных особых точек и , то

.

59). Найти особые точки и указать их характер (для полюсов определить их порядок)

а) ; б) ; в) ;

г) ; д) ; е) ;

60). Найти вычеты функций в их особых точках.

а) ; б) ; в) ;

г) ; д) ; е) ;

ж) ; з) ; и) ;

61). Найти ; если а) ; б) ; в) ;

62). Найти , где ;

63). Вычислить , где .

64). Найти , где .

65). Вычислить интеграл , где

66). Найти , где ;

67). Найти , где ;

68). Найти , если а) ; б) ; в) ;

69). Вычислить , где

70). Найти , где