Представление нагрузок с помощью рядов фурье

Рассмотрим случай действия заданных на верхней и нижней кромках балки-стенки нагрузок (рис. 2).

Рис. 2

Если на двух кромках заданы различные нагрузки , то их всегда можно заменить суммой двух нагружений: симметричного с нагрузками и антисимметричного с нагрузками , рис 2, причем:

(8)

6

В дальнейшем можно, например, считать нагрузки q и Т симметричными, а для антисимметричного загружения результаты получа­ются по аналогии с симметричным загружением. Это первое воз­можное упрощение решения задачи расчета балки-стенки.

Второе упрощение состоит в том, что нагрузки q(x) и T(x) не обязательно раскладывать в полные ряды (7). Возможно ограничиться разложением в ряд по синусам:

, (9)

или в ряд по косинусам:

. (10)

В обоих случаях при удержании достаточного числа членов ряда исходная нагрузка аппроксимируется рядами (9) или (10) с высо­кой степенью точности.

Рассмотрим конкретный пример для нагрузки с рис. 3.

Рис. 3

Подчеркнем, что, как на рис. 3, так и в вариантах заданий на расчетно-графическую работу нагрузки q(x) и T(x) являются кусочно-постоянными, рис. 4.

Рис. 4

7

Для нагрузки с рис. 4 а интегралы в (9), (10) вычисляются по формулам:

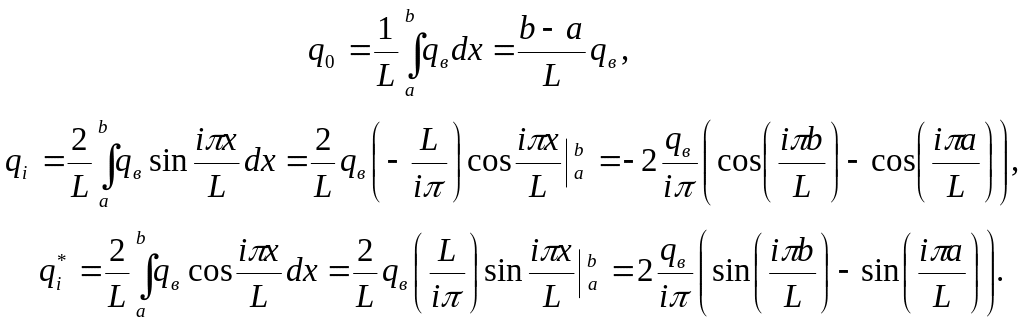(11)

Для нагрузки с рис. 4 б интегралы в (9), (10) имеют вид:

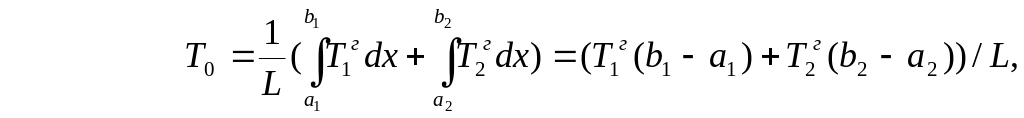(12)

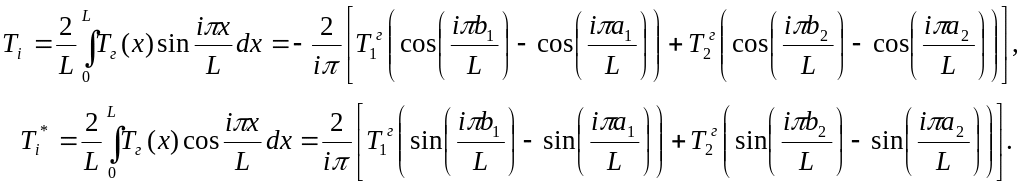
По формулам (11) получены коэффициенты разложения нагрузки c рис. 3 в ряды (9) и (10) и , представленные в табл. 1. Отметим, что известна и величина:

Таблица 1

i L			i			i
I	0,5151	0,2624	11	0,0468	-0,0919	21	0,0245	0,0125
2	0,4167	-0,3027	12	-0,0367	-0,0505	22	0,0379	-0,0275
3	-0,0656	-0,4140	13	-0,0151	0,0024	23	-0,0086	-0,0540
4	-0,2879	-0,0935	14	0,0087	-0,0267	24	-0,0480	-0,0156
5	-0,1273	0,1273	15	-0,0424	-0,0424	25	-0,0255	0,0255
6	0,0203	0,0237	16	-0,0720	0,0234	26	0,0047	0,0144
7	-0,0281	-0,0045	17	-0,0116	0,0731	27	-0,0073	-0,0012
8	-0,0550	0,0757	18	0,0463	0,0336	28	-0,0157	0,0216
9	0,0572	0,1123	19	0,0271	-0,0138	29	0,0178	0,0348
10	0,1273	0	20	0	0	30	0,0424	0

8

На рис. 5 а, б даны эпюры , полученные представлением исходной нагрузки (рис. 3) рядами (9) при m =30, рис. 5 а, и рядами (10) при m =30, рис. 5 б.

Эпюры рис. 5 а, б убедительно свидетельствуют о высокой точности аппроксимации локальной нагрузки при m = 30.

Очевидно, что при рассмотрении меньших номеров приближе­ний m в рядах (9) и (10) результаты аппроксимации ухудшаются, причем не только для локальных, но и для равномерно распределенных нагрузок.

Рис. 5

В качестве примера возьмем равномерно распределенную нагрузку . В табл. 2 даны величины коэффициентов разложения в ряды (9) и (10), причем известна и величина:

.

Таблица 2

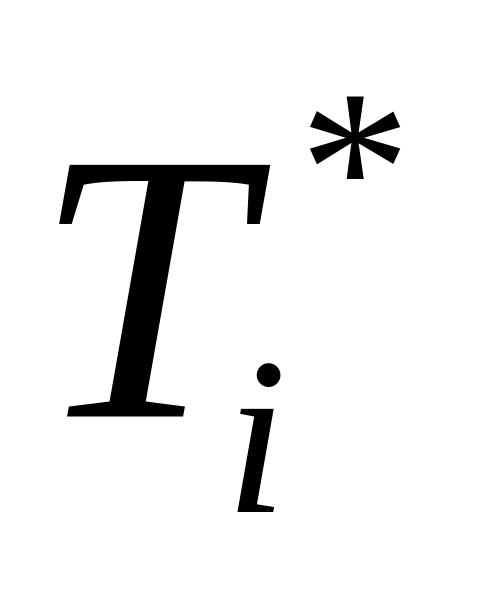
i			i
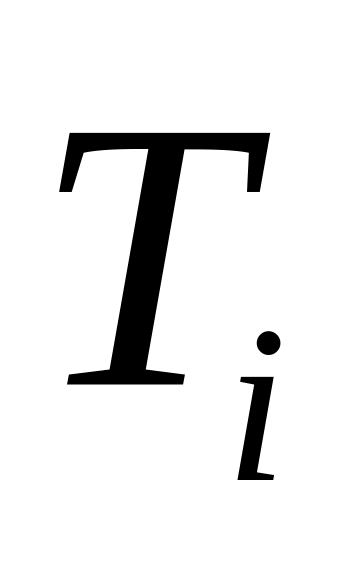
1	1,2723	0	6	0	0
2	0	0	7	0,1819	0
3	0,4244	0	8	0	0
4	0	0	9	0,1415	0
5	0,2546	0	10	0	0

Из табл. 2 видно, что для случая нагрузки, симметричной относитель­но , все кососимметричные гармоники имеют ну­левые коэффициенты, то есть , четное).

9

Левая половина симметричной относительно эпюры , аппроксимирующей при m = 10 исходную нагрузку , приведена на рис. 6.

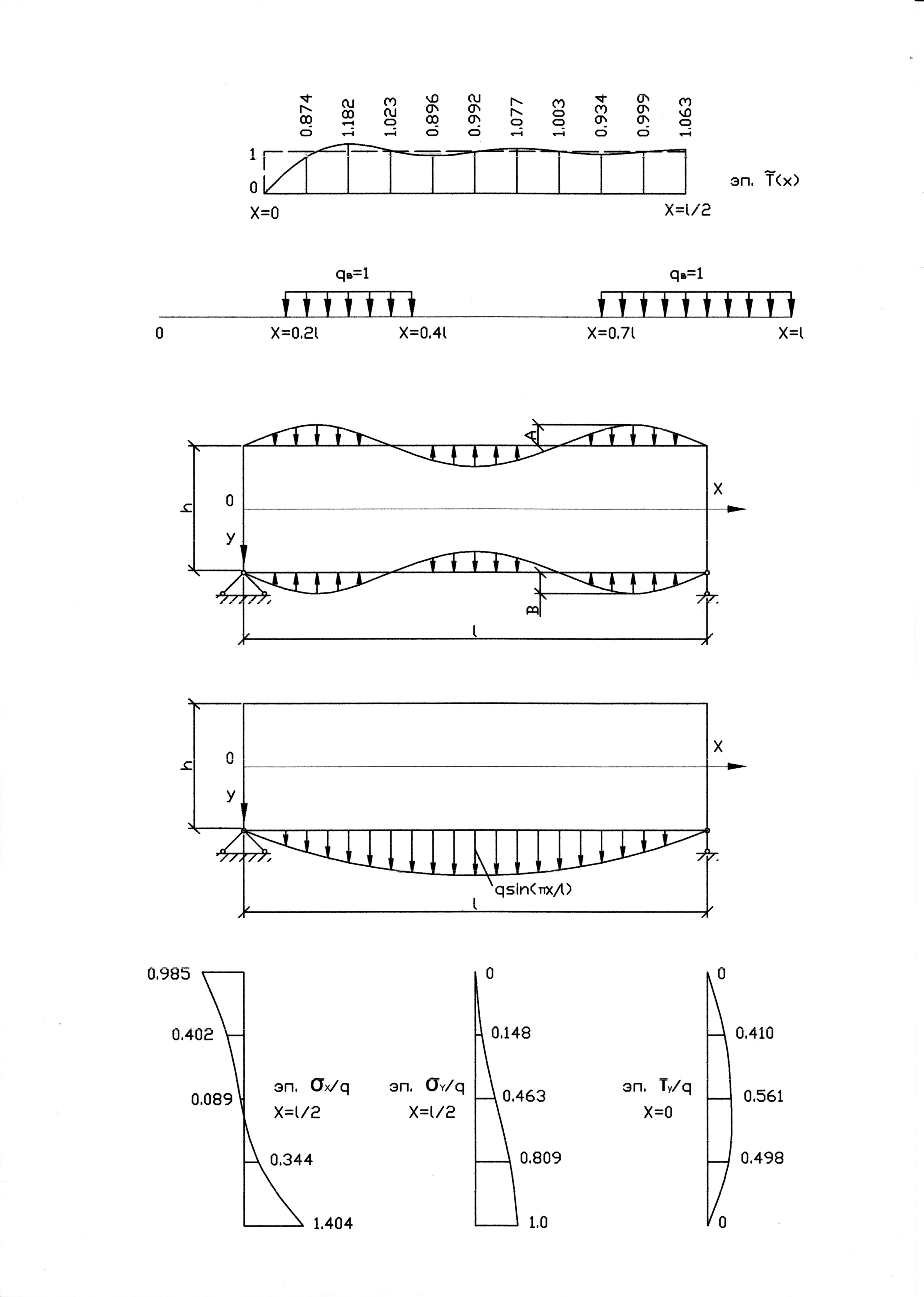
Рис. 6

Из сопоставления ординат эпюр нагрузок с рис. 6 и рис. 5 видно, что при m = 10 погрешности аппроксимации возрастают, несмотря на отсутствие локальности нагрузки .

Заметим, что в табл. 2 абсолютно четко прослеживается убы­вание величин коэффициентов ряда с ростом i, что непосредственно характери­зует сходимость приближенного решения к точному.

В табл. I проведение анализа сходимости сопряжено с определенными труд­ностями, связанными, в частности, со знакопеременностью величин и . Можно, тем не менее, установить, например, что , то есть решение по величинам сходится. Аналогичные неравенства можно записать для ве­личин , что определяет сходимость рядов (10).

При счете на ПЭВМ число членов ряда в линейной задаче мо­жет быть весьма большим, например, в [I , c.100] указывает­ся на решение задачи о действии на балку-стенку сосредоточенной силы с удержанием в рядах Фурье нечетных гармоник с .

В следующем разделе методических указаний исследу­ются вопросы, связанные с потерей точности вычислений при боль­ших величинах номеров гармоник i в (9), (10).

Для большинства реальных нагрузок в рядах (9) , (10) доста­точно удерживать существенно меньшее число членов ряда. Представляется разумным взять за критерий необходимой точности аппроксимации исходной наг­рузки отклонение в ±5%, совпадающее по величине с обычной инженерной точностью расчетов.

Рассмотрим в качестве примера нагрузку, изображенную на рис. 7, и определим для нее точность аппроксимации исходной кусочно-постоянной нагрузки полным рядом (7) при различных величинах m.

10

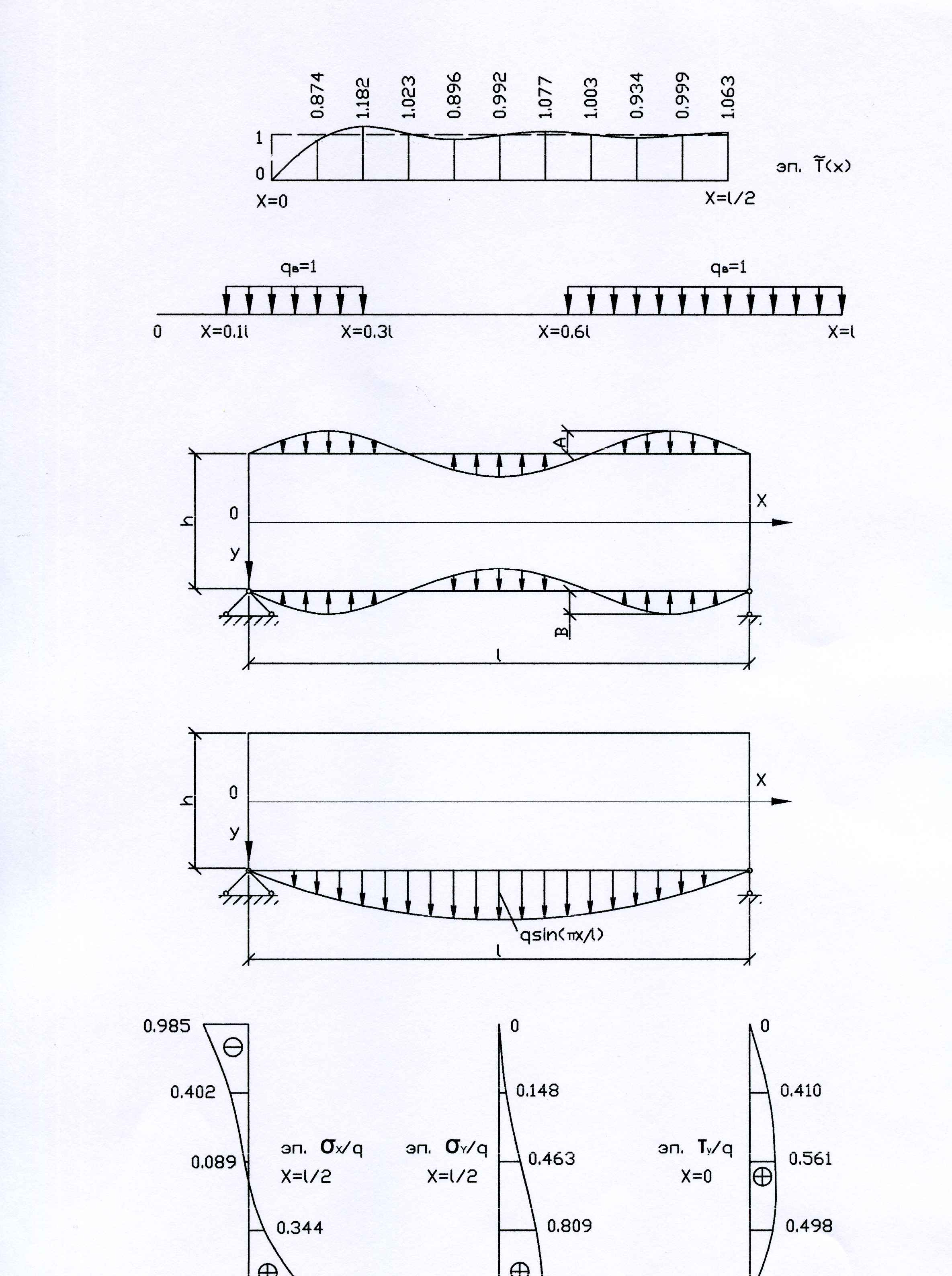
Рис. 7

В табл. 3 приведены ординаты эпюры q(x) по (7) в виде зна­чений для диапазона и значений для диапазона

Таблица 3

m
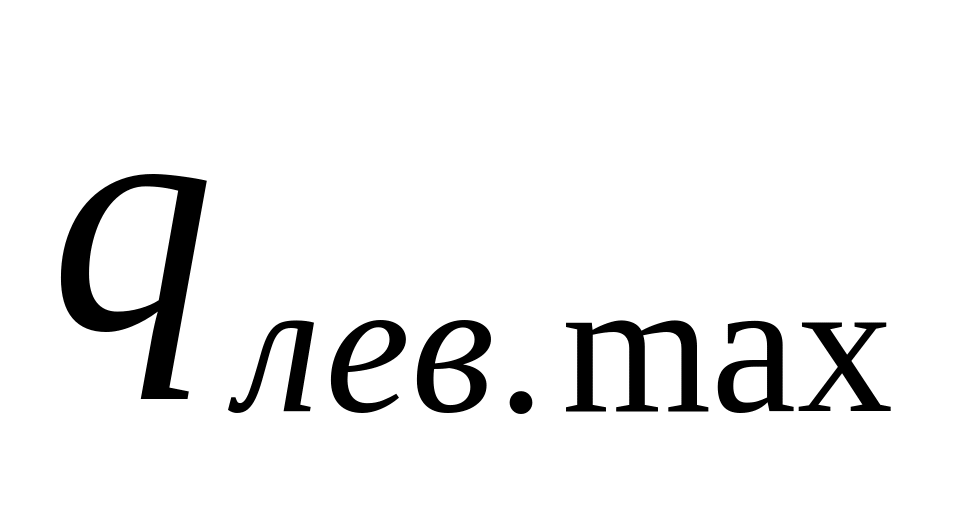
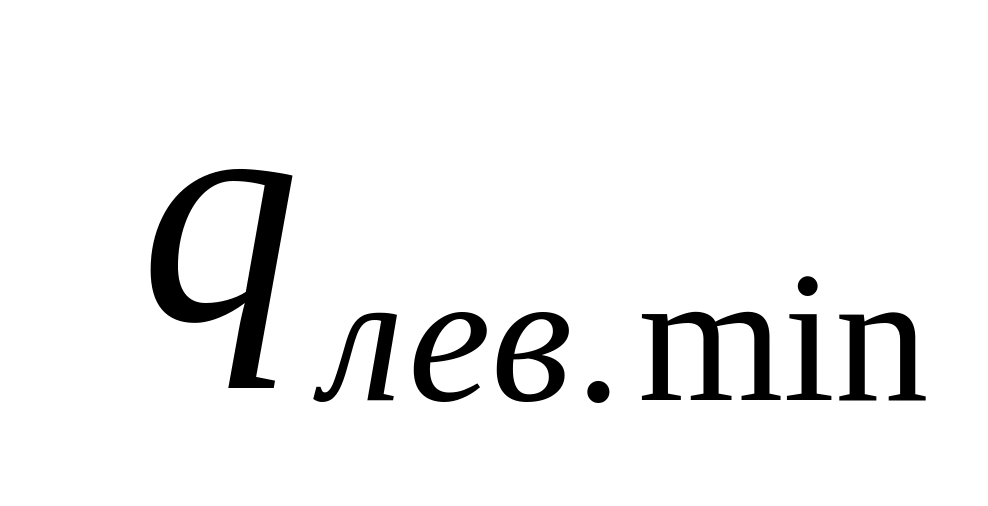
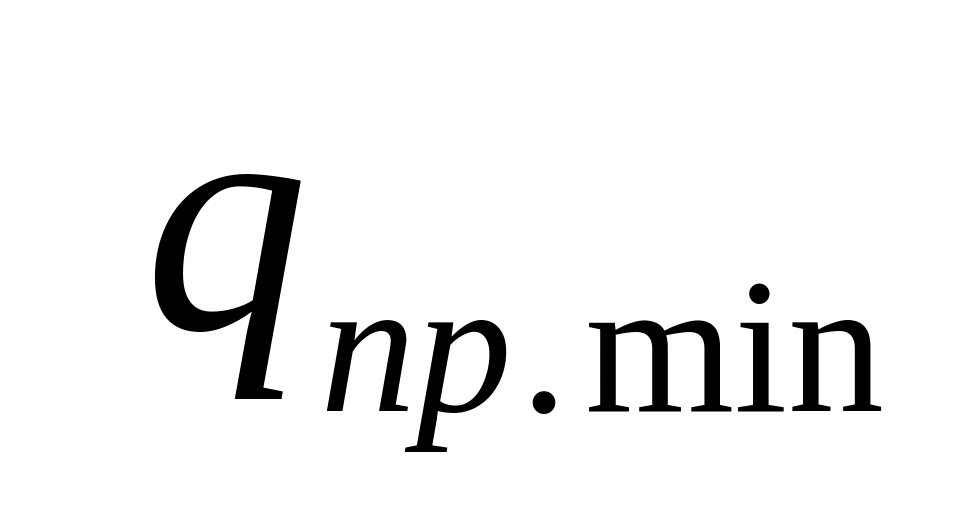
I	0,467	0,290	0,665	0,464
2	0,331	0,323	0,765	0,628
3	0,650	0,494 0,665	1,119	0,487
4	0,839	0,665	1,250	0,485
5	0,966	0,704	1,127	0,606
6	1,053	0,657	1,109	0,613
7	1,051	0,706	1,061	0,663

Отметим, что наблюдаются вблизи концов участков с дей­ствующей нагрузкой . Из данных табл. 3 видно, что уже приближе­ние m = 7 дает приемлемую точность аппроксимации исходной нагрузки. Очевидно, что при решении в приближении с m = 7 следует ожидать точности вычисления напряжений также в пределах около 5%, что вполне достаточно для инженерных расчетов балок-стенок.

Подчеркнем, что при рассмотрении приближений с m = 7 в (7), (9), (10) не происходит потери точности вычислений. Это позволяет при программировании для ПЭВМ всех расчетных формул ограничиться точностью вычислений REAL.

В связи с этим при выполнении расчетно-графической работы необходимо вычислить , (i = 1,2,...,20) и после это­го оценить точность аппроксимации исходной нагрузки (или ) при различных значениях m.

Отметим, что формулы (9), (10), (11), (12) поддаются элементарному программированию на любом проблемно-ориентиро­ванном языке. В приложении 1 к методическим указаниям приведе­на схема алгоритма вычисления величин по формулам (11) , (12) и построения эпюр по формулам (9), (10). Данная схема без изменений применима и к тангенциальным наг­рузкам .

11

Кроме того, заметим, что и при использовании микрокальку­лятора требуемый объем вычислений также невелик: при построе­нии эпюр или достаточно разбивать отрезок распределения нагрузки на 4 части.

Результатом вычислений коэффициентов рядов (9), (10) и оценки необходимого числа m в (9), (10) должно являться заключение о наименьшем необходимом числе членов ряда, дающем требуемую точность аппроксимации заданной нагрузки на балку-стенку.

В соответствии с рекомендациями [1] предпочтитель­нее раскладывать в ряд (9) по синусам, a - в ряд (10) по косинусам.

Чрезвычайно важно, что решение на каждый из членов ряда (9) или (10) на основе принципа суперпозиции (независимости действия сил) может быть получено отдельно с последующим суммированием ре­зультатов. Это также выгодно отличает предлагаемый алгоритм расчета балки-стенки.