4. Обратное пространство и обратная решётка

Каждой кристаллической структуре соответствуют две решетки ‑ прямая кристаллическая решетка и обратная решетка, которая строится следующим образом:

1) если обычная прямая решетка построена на векторах трансляций ,  ,  , то оси обратной к ней решетки ,  ,  определяются как векторные произведения:

; (4.1)

2) осевые параметры обратной решетки ,  ,  равны обратным величинам межплоскостных расстояний плоских сеток прямой решетки, нормальных к этой оси.

Каждой плоскости (hkl) прямой решетки отвечает в обратной решетке узел [[hkl]]*. Бесконечному семейству параллельных плоскостей {hkl} в пространстве прямой решетки соответствует в пространстве обратной решетки бесконечное семейство точек [[hkl]]* вдоль направления, нормального к этим плоскостям. Расстояния этих точек от точки, принятой за начало координат в обратном пространстве, равны 1/d, 2/d, 3/d,..., где d = d_hkl ‑ расстояние между плоскостями {hkl} в прямой решетке (рис. 11).

Рис. 11. Прямая (а) и обратная (б) решетки

Зоне плоскостей прямой решетки отвечает сетка из точек (узлов) обратной решетки, причем ось зоны прямой решетки нормальна к плоскости сетки обратной решетки. Наконец, прямой пространственной решетке из плоскостей {hkl} отвечает обратная трехмерная решетка из точек [[hkl]]*. Основные векторы ,  ,  обратной решетки определяются векторными произведениями (4.1) или скалярными произведениями:

а*а =b*b = с*с = 1, а*b = а*с = b*с = b*а = с*b = с*а = 0. (4.2)

Из равенств (4.1) видно, что вектор нормален к плоскости векторов и и т.д. Тройка векторов ,  ,  выбирается так, чтобы они, как и векторы ,  ,  , составляли правую тройку.

Векторы ,  ,  представляют собой площадки элементарных параллелограммов в координатных плоскостях прямой решетки, а по абсолютному значению они обратно пропорциональны межплоскостным расстояниям прямой решетки:

(4.3)

(в знаменателе ‑ смешанное произведение векторов).

Прямая и обратная решетки сопряжены взаимно, т.е. решетка, построенная на осях ,  ,  , является обратной по отношению к решетке ,  ,  , а решетка, построенная на векторах ,  ,  , ‑ обратной по отношению к решетке ,  ,  .

Основные свойства обратной решетки

1. Вектор обратной решетки перпендикулярен плоскости (hkl) прямой решетки, а длина этого вектора равна обратной величине расстояния d между плоскостями {hк1} прямой решетки, т.е.

. (4.4)

2. Объем V* элементарной ячейки обратной решетки равен обратной величине объема V элементарной ячейки прямой решетки (и обратно):

; . (4.5)

Можно показать, что кубической объемно-центрированной решетке соответствует обратная кубическая гранецентрированная.

Миллеровские индексы системы параллельных плоскостей прямой решетки являются координатами ряда обратной решетки.

Физический смысл обратной решетки

Понятие об обратной решетке вводится в основном для описания периодического распределения отражающей способности кристалла по отношению к рентгеновским лучам.

Отражение рентгеновских лучей от плоскостей структуры кристалла описывается формулой Вульфа — Брэгга (см. вывод формулы Вульфа-Брэгга, стр. 9)

,

где λ ‑ длина волны рентгеновского излучения, θ ‑ угол, дополнительный до 90° к углу падения (или к углу отражения), d ‑ межплоскостное расстояние для семейства параллельных отражающих плоскостей, п ‑ порядок дифракционного спектра.

Из условия Вульфа ‑ Брэгга следует, что при постоянной λ, большому d отвечает малый угол θ, т. е. чем больше межплоскостное расстояние, тем ближе направления отраженных лучей к направлению падающего пучка. Отражения рентгеновских лучей от бесконечно протяженных идеальных кристаллов должны быть точечными.

Каждый узел обратной решетки соответствует возможному отражению от плоскостей прямой решетки кристалла. Направление вектора обратной решетки H^*_hkl совпадает с направлением отражения от плоскостей {hkl}, а n-й узел обратной решетки в этом ряду отвечает отражению n-го порядка от этих плоскостей.

На основании представления об обратной решетке Эвальдом дано построение, позволяющее наглядно геометрически истолковать пространственное распределение отражений рентгеновских лучей от кристалла. Построение Эвальда дает возможность решать основную задачу рентгеноструктурного анализа: определять, возникнут ли дифрагированные лучи и в каких направлениях, если на кристалл падает пучок рентгеновских лучей с длиной волны λ.

П

Рис. 12. Построение Эвальда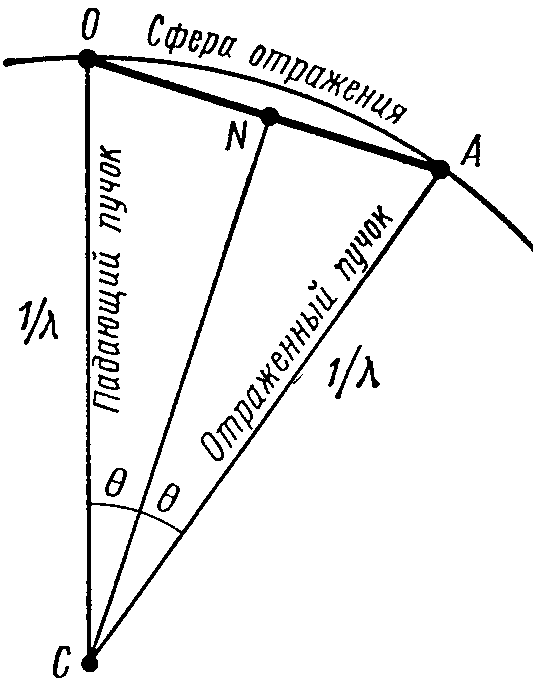

усть рентгеновский пучок падает на кристалл в направлении CO (рис. 12), CN ‑ направление r^*_hkl, т. е. нормаль к плоскостям {hkl}.

Примем точку О за начало координат обратной решетки и проведем из точки С сферу радиусом 1/λ ‑ так называемую сферу отражения, или сферу Эвальда. Если сфера Эвальда пройдет через другой узел А обратной решетки, то направление СА есть возможное направление дифрагированного луча данной падающей волны. В самом деле,

ОС = АС= 1/λ, ОN = АО/2 = п/(2d), ,

отсюда получаем уже известную нам формулу

Таким образом, закон Вульфа ‑ Брэгга удовлетворяется для любого узла обратной решетки, находящегося на сфере Эвальда.

Вывод формулы Вульфа-Брегга

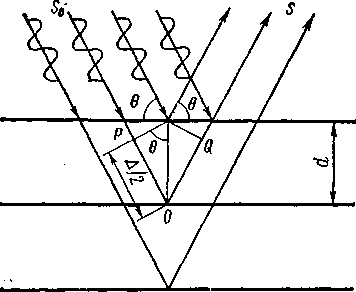
Рис. 13. К выводу условия Вульфа – Брэгга

Грани кристаллического многогранника соответствуют определенным сеткам структуры, поэтому углы между гранями отвечают углам между плоскими сетками в структуре кристалла. Теперь эти углы измеряют с помощью рентгенограмм, для чего не обязательно иметь большой кристалл с правильной внешней огранкой, а достаточно крупинки кристаллического вещества. Поскольку длины волны рентгеновского излучения соизмеримы с межатомными расстояниями в кристаллических структурах, кристаллы являются природными дифракционными решетками. Именно с помощью дифракции рентгеновских лучей было доказано решетчатое строение кристаллов (М. Лауэ, 1912). Схема, поясняющая дифракцию, дана на рис. 3: S₀ ‑ пучок монохроматических рентгеновских лучей, падающих под углом θ на семейство параллельных атомных плоскостей, S ‑ пучок дифрагированных лучей. Дифрагированные лучи усиливают друг друга, если согласно условию интерференции разность хода Δ между ними равна целому числу длин волн, т.е.

Δ=nλ (n = 1,2,3, …)

Из чертежа видно, что разность хода между падающим и дифрагированным лучами равна

Δ= РО + OQ = 2РО = 2dsinθ.

Чтобы волны, рассеянные двумя соседними плоскими сетками (а значит, и всем семейством параллельных плоских сеток), дали максимум интенсивности, необходимо выполнение основного закона дифракции рентгеновских лучей в кристаллах:

2dsinθ = пλ (n = 1, 2, 3, ...) (*)

Это равенство выражает условие Вульфа — Брэгга.

Иначе говоря, если луч с длиной волны λ, падает на совокупность параллельных атомных плоскостей, отстоящих друг от друга на расстояний d, то он порождает дифрагированный луч, идущий так, как шел бы луч, отраженный под углом θ. Таким образом, при определенных углах падения плоские сетки в структуре кристалла могут «отражать» рентгеновские лучи. Эти отражения (точнее, максимумы интенсивности дифрагированных лучей) можно зарегистрировать на фотографической пластинке с помощью ионизационного спектрометра. Симметричный, закономерный узор на рентгенограмме, например рис. 4, отображает симметрию и закономерность структуры кристалла и дает возможность измерять расстояния между атомными плоскостями и углы между ними, которые на многогранных формах кристаллов являются углами между гранями. По рентгенограммам на основании условия (*) можно изучать структуры кристаллов, находить межплоскостные расстояния d, диагностировать кристаллические вещества.

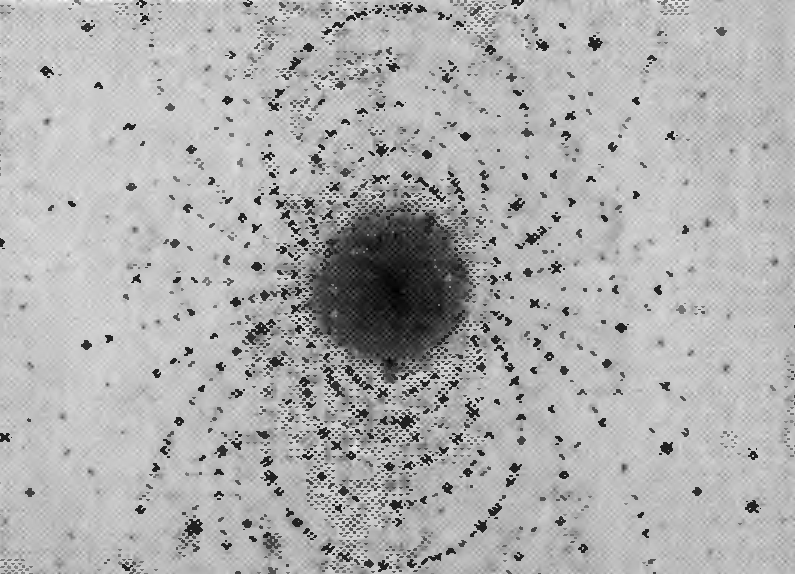
Рис.14. Рентгенограмма кристалла.