
- •Затверджено
- •Зміст дисципліни за темами
- •Тема 1. Сутність та основні функції ризику
- •Зміст теми.
- •Тема 2. Причини виникнення та класифікація ризику
- •Зміст теми.
- •Тема 3. Якісний та кількісний аналіз ризику
- •Зміст теми.
- •Тема 4. Система кількісних оцінок ризику
- •Зміст теми.
- •Тема 5. Відносна оцінка ризиків на основі аналізу фінансово-економічного стану підприємства
- •Зміст теми.
- •Інтерпретація результатів розрахунку z-показника
- •Тема 6. Концепція корисності та оптимізація ризику
- •Зміст теми.
- •Тема 7. Основні засади моделювання ризику на основі теорії ігор
- •Зміст теми.
- •Тема 8. Моделювання ризику при різних рівнях заданого розподілу ймовірностей
- •Зміст теми.
- •Тема 9. Формування інвестиційної стратегії підприємства з урахуванням ризику
- •Зміст теми.
- •Тема 10. Основні підходи до процесу управління ризиком
- •Зміст теми.
- •Практичні завдання.
- •Практичні завдання.
- •Заняття 4. Аналітична оцінка ризику на основі ідентифікації фінансово-економічного стану підприємства
- •Основні питання.
- •Ділова гра
- •Заняття 5. Прийняття рішень в умовах ризику на основі теорії корисності
- •Основні питання.
- •Теми доповідей.
- •Проблемні ситуації для обговорення.
- •Практичні завдання.
- •Рекомендована література Основна література
- •Додаткова література
Тема 8. Моделювання ризику при різних рівнях заданого розподілу ймовірностей
Основні питання:
1. Критерії прийняття рішень при заданому розподілі ймовірностей.
2. Критерії прийняття рішень за умов відсутності розподілу ймовірностей.
3. Суперпозиція критеріїв прийняття рішень, обтяжених ризиком.
Мета теми: опрацювання теорії математичних моделей та методів прийняття раціональних рішень за умов заданого розподілу ймовірностей.
Основні терміни і поняття теми: критерій Байєса, критерій Бернуллі-Лапласа, математичне сподівання, антагоністичні інтереси середовища.
Зміст теми.
Згідно з критерієм Байєса (критерій ризику) оптимальним розв’язком слід вважати такий, для якого математичне сподівання функціоналу оцінювання досягає свого найменшого значення:
![]() ,
(36)
,
(36)
де
-
величина ризику функціоналу оцінювання
![]()
Етапи розрахунку критерію:
розраховується матриця ризиків;
розраховуються величини
 ,
які називають Байєсовським ризиком
для розв’язку
,
які називають Байєсовським ризиком
для розв’язку
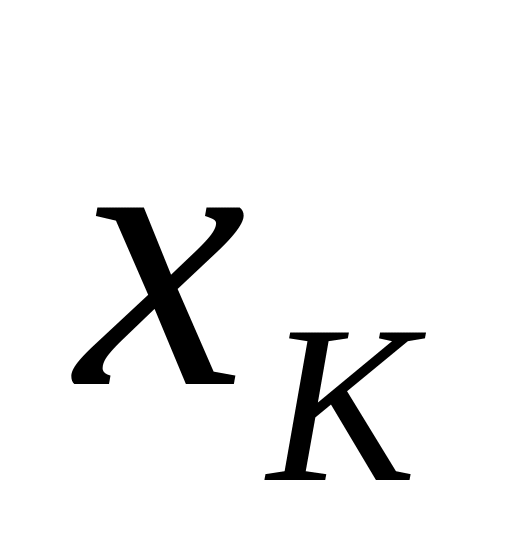 .
.з отриманих значень обирають мінімальне.
Отже, оптимальним є варіант, який забезпечує підприємству мінімальний допустимий ризик.
Існує інший варіант застосування критерію Байєса, який задовольняє умові:
![]() (37)
(37)
Тобто, знаходиться математичне сподівання для кожного рішення на основі вихідної матриці прибутків і обирається серед них максимальне.
Згідно
з критерієм
Бернуллі-Лапласа
апріорні ймовірності
![]() станів середовища рівні, тобто згідно
з «принципом недостатніх підстав»:
станів середовища рівні, тобто згідно
з «принципом недостатніх підстав»:
![]() .
.
Ці оцінки розподілу апріорних ймовірностей дають змогу застосувати критерії інформаційної ситуації . Критерій Бернуллі-Лапласа, що ґрунтується на застосуванні критерію Байєса та принципу недостатніх підстав для знаходження оцінок апріорних ймовірностей , формулюють так: оптимальним є той розв’язок , який задовольняє умові:
![]() ,
(38)
де
,
(38)
де
![]() ,
(39)
,
(39)
n – кількість станів економічного середовища.
Етапи розрахунку даного критерію:
розраховується матриця кількісної оцінки ризику;
визначається середнє математичне очікування ризиків;
із отриманих даних обирається мінімальне.
Іншим способом визначення оптимального варіанту за даним критерієм є вибір рішення яке задовольняє умові:
![]() ,
(40)
,
(40)
де
![]() (41)
(41)
Тобто, за основу розрахунків береться вихідна матриця прибутків.
В
ситуації, коли мається апріорний розподіл
ймовірностей настання певного стану
![]() і водночас йдеться про антагоністичні
інтереси середовища
і водночас йдеться про антагоністичні
інтереси середовища
![]() ,
що мають для керівництва фірми пріоритет,
то має місце інформаційна ситуація
,
при якій за критерій прийняття рішення
обирається критерій
Гурвіца.
,
що мають для керівництва фірми пріоритет,
то має місце інформаційна ситуація
,
при якій за критерій прийняття рішення
обирається критерій
Гурвіца.
Етапи розрахунку критерію:
визначається мінімальне значення функціоналу оцінювання для кожного рядку вихідної матриці;
для кожного рішення визначається
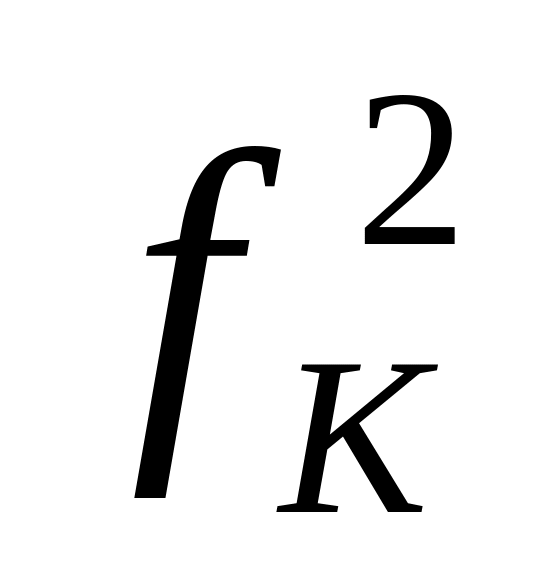 ;
;для кожного рішення визначається
 ;
;із отриманих значень обирається максимальне.
Критерій
Гурвіца має назву песиміста-оптиміста.
При
![]() критерій Гурвіца співпадає з максимальним
критерієм, а при
критерій Гурвіца співпадає з максимальним
критерієм, а при
![]() - з критерієм Вальда.
- з критерієм Вальда.
За іншими методиками (за відсутності ймовірностей розподілу станів середовища) на основі матриці прибутків критерій Гурвіца визначається згідно умови:
![]() ,
(42)
,
(42)
а на основі ризиків:
![]() (43)
(43)
Якщо в умові задачі є ймовірність (Р) появи стану середовища (Q), то критерій Гурвіца слід розраховувати з використанням (на основі) критерію Байєса.
Якщо ймовірності не вказані, слід скористатися формулами (42) та (43).
Література: 1, с. 166-188; 3, с. 205-256; 5, с. 256-300; 10, с. 106-119
