Основні питання.

1. Концепція пріоритетів в теорії корисності, їх формалізація.

2. Методологія застосування лотереї за Нейманом-Моргенштерном для здійснення альтернативного вибору в умовах ризику.

3. Особливості формування ставлення особи до ризику та приклади їх застосування в різних сферах суспільного життя.

4. Вибір та обґрунтування рішення на основі теорії корисності за різних типів ставлення особи до ризику.

Теми доповідей.

1. Методи побудови функцій корисності та приклади їх реалізації.

2. Використання функцій несхильності до ризику під час прийняття рішень.

Проблемні ситуації для обговорення.

1. Який існує зв’язок між прийняттям рішень в умовах економічного ризику та кількісними властивостями корисності?

2. В яких сферах економічного життя застосовується теорія різного відношення особи до ризику?

3. Яким чином величина детермінованого еквіваленту ідентифікує відношення особи до ризику?

Практичні завдання.

Задача 1. Нехай U (x) = a + bx, b>0. Припустимо, що особа, яка приймає рішення, має справу з лотереєю, що має щільність розподілу f (х). Необхідно визначити сподіваний виграш, детермінований еквівалент та премію за ризик.

Задача 2. Обчислити сподіваний виграш, детермінований еквівалент та премію за ризик для лотереї L(4;0,5;12), якщо функція корисності має вигляд . Визначити відношення особи до ризику.

Задача 3. Визначити премії за ризик для лотерей L(0;0,5;10) та L(20;0,5;30), якщо функція корисності має вигляд .

Задача 4. Особа, яка є схильною до ризику, має зростаючу функцію корисності і повинна обрати нове місце роботи з двох альтернативних варіантів. У першому випадку її невизначений доход може становити 1 тис. грн. з ймовірністю 0,5 або 3 тис. грн. з тією самою ймовірністю. У другому місці їй пропонується детермінований доход у 2 тис. грн. Яке місце роботи доцільно обрати даній особі?

Задача 5. Підприємець, функція корисності якого задана як , вирішує, як йому краще використати частину свого капіталу розміром 100 тис. грн.

Ці кошти він може:

а) покласти в банк на депозитний рахунок з фіксованим доходом 15% на рік;

б) вкласти в угоду і отримати прибуток розміром 50% від вкладених коштів, але ймовірність одержання такого прибутку становить 0,4.

Як підприємцю доцільніше використати свій капітал? Обчисліть премію за ризик і розкрийте її економічну сутність.

Задача 6. Двоє студентів у вихідний день вирішили сходити на іподром, маючи в своєму розпорядженні по 50 грн. Перед черговим заїздом вони почали радитись – робити їм ставки чи ні:

а) можна спостерігати за видовищем і зберегти свої гроші;

б) можна зробити ставку в черговому заїзді і при цьому або програти свої гроші з ймовірністю 0,5, або отримати виграш у співвідношенні 1:3 (також з ймовірністю 0,5).

Яке рішення прийме кожний студент, якщо один з них має функцією корисності , а другий - .

Охарактеризуйте цих студентів з огляду їх ставлення до ризику.

Заняття 6. Моделювання економічного ризику та теорія ігор

Мета заняття: опрацювання методики прийняття економічних рішень з оптимальним ступенем ризику в ситуаціях невизначеності за умов широкого спектру норм прибутку.

Основні питання.

1. Понятійний апарат теорії гри.

2. Моделювання ризику в умовах антагоністичних інтересів середовища за критеріями Вальда та Севіджа.

3. Оптимізація вибору при різних рівнях заданого розподілу ймовірностей за критеріями Байєса, Бернуллі –Лапласа та Гурвіца.

4. Особливості застосування в практичній діяльності основних критеріїв теорії гри.

Теми доповідей.

1. Використання теоретико-ігрової моделі в теорії портфеля та можливі підходи до вирішення цієї проблеми.

2. Сценарний аналіз розвитку політичного ризику та використання теорії гри.

3. Застосування теорії ігор при виборі альтернативних варіантів управлінського рішення.

Проблемні ситуації для обговорення.

1. Чому під час прийняття економічних рішень виникають багатокритеріальні задачі? Поясніть їх сутність.

2. Які принципи покладено в основу класифікації інформаційних ситуацій?

3. Чи можна вважати, що критерій Гурвіца є зваженою комбінацією двох критеріїв? Яких? Поясніть свою думку.

Практичні завдання.

Задача 1. Нехай функціонал оцінювання відображає обсяг виручки, яку може отримати банк від реалізації акцій чотирьох компаній (Х_і) залежно від станів економічного середовища (Q_j) (у млн. грн.). Вихідні дані наведено у таблиці.

Варіант рішення	Стани економічного середовища
	6,0	6,2	5,5
	7,5	7,1	7,0
	7,4	7,5	8,0
	7,0	5,8	6,0

Відомо, що стани економічного середовища можуть реалізуватися, відповідно, з ймовірностями =0,3; =0,5; =0,2. Оберіть оптимальне рішення згідно з критерієм Байєса.

Задача 2. Фірма має кілька каналів продукції певного асортименту.

Невизначеність у ймовірних коливаннях попиту на продукцію цієї фірми зумовлена ступенем залежності від змін кон’юнктури ринку. Мається три стратегії виробництва продукції: 2000 тис. грн., 3000 тис. грн., 4000 тис. грн. Залежно від змін кон’юнктури ринку фахівці фірми розрахували варіанти середньорічного прибутку. Ці варіанти подані у вигляді матриці платоспроможності з урахуванням сподіваних значень збитків, що пов’язані з зберіганням нереалізованої продукції:

Обсяг виробництва	Розмір прибутку залежно від попиту
	1000	2000	3000	4000
2000	340	1400	1400	1400
3000	-20	1040	1400	1400
4000	-380	680	1740	2800

Обрати оптимальну для даного підприємства стратегію за критеріями Вальда і Севіджа.

Задача 3. Фірма ставить за мету вихід на міжнародний ринок зі своєю продукцією. Її фахівцями опрацьовано чотири варіанти рішень щодо випуску продукції. Вибір рішення залежить від попиту який може подаватися трьома варіантами , , . Функціонал оцінювання (прибуток у млн. грн.) подано в таблиці.

Варіант рішення	Стани економічного середовища
	2,0	3,0	1,5
	7,5	2,0	3,5
	2,5	8,0	2,5
	8,0	5,0	4,5

Відомо, що стан може реалізуватися з ймовірністю =0,1; - з ймовірністю =0,5; - з ймовірністю =0,4. Водночас фірма впевнена, що зіштовхнеться з конкурентами, вплив яких очікується з вагою . Обрати оптимальне рішення з допустимим рівнем ризику на основі критерію Гурвіца.

Задача 4. При переході на випуск нових видів продукції опрацьовано чотири варіанти рішення: .

Результати вибору залежать від ймовірного стану економічного середовища, яке може бути одним з чотирьох варіантів: , а ймовірність настання кожного з них оцінюється як =0,3; =0,1; =0,5, =0,1. Відомий також функціонал оцінювання (наприклад, затрати на виробництво продукції, тис. грн.).

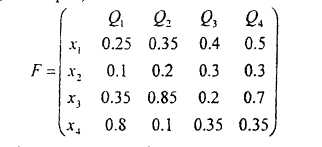
Урахувавши можливість конкуренції з певним ваговим коефіцієнтом , визначити оптимальну стратегію підприємства щодо випуску нових видів продукції.

Заняття 7. Диверсифікація як спосіб зниження ризику: елементи теорії портфеля

Мета заняття: оволодіння студентами практичними навичками формування оптимального портфеля цінних паперів.

Основні питання.

1. Теорія портфеля: сутність та сфери використання.

2. Визначення норми прибутку цінних паперів.

3. Методика формування портфелю з двох різних акцій.

4. Формування портфелю з багатьох акцій.

Теми доповідей.

1. Арбітражна теорія портфеля.

2. Використання теорії портфеля під час створення запасів матеріалів на підприємстві.

Проблемні ситуації для обговорення.

1. З якою метою, де і за яких умов використовувати диверсифікацію?

2. До розв’язання яких проблем та в яких сферах економіки можна застосовувати теорію портфеля?

3. Як обчислити структуру портфеля з двох цінних паперів, якщо міру його допустимого ризику задано?

Практичні завдання.

Задача1. Сподівана норма прибутку акцій виду становить 60%, ризик цих акцій (середньоквадратичне відхилення) – 20%. Для акцій виду сподівана норма прибутку – 40%, ризик – 15%. Коефіцієнт кореляції для цих акцій . На основі цих акцій створюється портфель цінних паперів.

Необхідно:

а) обчислити сподівану норму прибутку та ризик портфеля цінних паперів, якщо акції виду складають 20% вартості цього портфеля;

б) обчислити сподівану норму прибутку та ризик портфеля цінних паперів, якщо акції виду складають 80% вартості цього портфеля;

в) створити оптимальний портфель цінних паперів (тобто такий, який має мінімальний ризик).

Задача 2. Виходячи з умов задачі 1, знайти структуру портфеля цінних паперів:

а) сподівана норма прибутку якого становила б 50%;

б) ризик якого становив би 16%.

Задача 3. Сподівані норми прибутку акцій виду становлять відповідно 60%, 50%, 40%, 70%. Ризики цих акцій відповідно становлять 40%, 30%, 25% та 50%. Тісноту зв’язку між нормами прибутку цих акцій відображають коефіцієнти кореляції =0,2; =-0,3; =-0,5; =0,9; =0,7; =-0,3. Необхідно сформувати з цих акцій портфель цінних паперів, що має мінімальний ризик. Оцінити його сподівану норму прибутку та його ризик.

Задача 4. Акції виду мають, відповідно, сподівані норми прибутку 20%, 40% та 60%, середньоквадратичні відхилення 10%,18% та 30%, коефіцієнти кореляції =1; =-1; =-1. Необхідно:

а) побудувати множини допустимих та ефективних портфелів цінних паперів;

б) визначити структуру портфеля цінних паперів, що має найбільшу сподівану норму прибутку при мінімальному ризику;

в) визначити сподівану норму прибутку та величину ризику для отримання портфеля цінних паперів.

Задача 5. Акції виду мають, відповідно, сподівані норми прибутку 10%, 20% та 50%, середньоквадратичні відхилення 2%,10% та 20%, коефіцієнти кореляції =0; =0; =-0,6. Необхідно:

а) побудувати множини допустимих та ефективних портфелів цінних паперів;

б) визначити оптимальну структуру портфеля цінних паперів щодо збереження капіталу;

в) визначити оптимальну структуру портфеля цінних паперів щодо збільшення приросту капіталу при ;

ж) визначити оптимальну структуру портфеля цінних паперів щодо максимального збільшення приросту капіталу при ;

з) для всіх отриманих портфелів цінних паперів обчислити сподівану норми прибутку та величину ризику.

Заняття 8. Практичні аспекти управління ризиком

Мета заняття: оволодіння практичними навичками оптимізації ризику на основі опрацювання суперпозиції способів зниження ризиків залежно від рівня можливих збитків та ймовірності їх отримання.

Основні питання.

1. Зміст та принципи управління ризиком.

2. Механізм реалізації зовнішніх способів зниження ризику.

3. Особливості застосування внутрішніх способів зниження ризику.

4. Методологія формування суперпозиції способів зниження ризику.

Теми доповідей.

1. Світовий досвід управління ризиком.

2. Можливості застосування зовнішніх та внутрішніх способів зниження ризику в умовах функціонування українських підприємств.

Проблемні ситуації для обговорення.

1. Які принципи використовуються на практиці при прийнятті управлінського рішення в умовах ризику?

2. Які способи зниження ризику, зовнішні чи внутрішні є надійнішими? Чому?

3. Які наслідки для підприємства матиме некерованість ризиків? Чи така ситуація є можливою в ринкових умовах господарювання?

Практичні завдання.

Задача 1. У зв’язку із можливими перебоями в постачанні енергетичних ресурсів недовиконання плану виробництва може становити: виробів А – 40 одиниць і виробів Б – 55 одиниць. Ціна за одиницю виробів становить відповідно 450 і 600 грн. Прибуток (у процентах до собівартості) становить 10%, умовно – постійні затрати – відповідно 150 і 200 грн. Визначити величину втрат від можливого зниження виробництва і реалізації продукції та запропонувати інваріантні способи зниження ризику.

Задача 2. У результаті посилення конкурентної боротьби можливе зниження цін становитиме: на виріб А – 15 грн., на виріб Б – 8 грн. Ціна за одиницю виробів становитиме відповідно 450 і 600 грн. Випуск продукції згідно із завданням складає: виробів А – 125 од., виробів Б – 94 од.

Визначити величину втрат від імовірного зниження цін та запропонувати інваріантні способи розв’язання ризику.

Задача 3. Виробнича програма заводу становить 600 одиниць виробів. Планові затрати на 1 виріб матеріалу А становлять 14 кг, матеріалу Б – 21 кг. У зв’язку з можливою зміною технологічного процесу з другого півріччя поточного року (має місце рівномірний розподіл виробничої програми за місяцями) матеріальні затрати зростуть відповідно на 0,5 і 0,6 кг у розрахунку на 1 виріб. Початкові (планові) ціни за 1 кг матеріалу А – 2,5 грн. і матеріалу Б – 1,9 грн. Розрахувати можливий розмір перевитрати матеріальних ресурсів та запропонувати інваріантні способи розв’язання ризику.

Задача 4. Продавець приватної крамниці (оптовий покупець) стоїть перед дилемою, яку кількість товару слід закупити: 1000 чи 2000 одиниць? При купівлі оптом 1000 одиниць товару затрати становитимуть 200 тис грн. за одиницю, а при купівлі 2000 одиниць – 180 тис грн. за одиницю. Підприємець буде продавати товар по 300 тис грн. за одиницю. Але він не знає, чи буде попит на даний товар. Весь не реалізований протягом відомого терміну товар можна буде реалізувати дещо пізніше, але лише по ціні 100 тис грн. за одиницю. Одержана інформація, на базі якої ймовірність того, що попит складе 1000 одиниць, становить 0,5, а ймовірність того, що попит буде на рівні 2000 одиниць, дорівнює теж 0,5. Рішення прийняти на основі обчислення вартості додаткової інформації про попит на даний товар.