Тема 9. Формування інвестиційної стратегії підприємства з урахуванням ризику

Основні питання:

1. Сутність та сфери застосування теорії портфелю.

2. Формування портфелю з двох різних акцій.

3. Портфель з багатьох акцій.

4. Оптимізація структури портфелю.

5. Спрощена класична модель формування портфелю.

Мета теми: побудова оптимальних портфелів цінних паперів.

Основні терміни і поняття теми: портфель цінних паперів, диверсифікація вкладень, множина допустимих портфелів, множина ефективних портфелів, оптимальний портфель, структура портфеля цінних паперів.

Зміст теми.

Під теорією портфеля розуміють розподіл коштів між цілим рядом різних активів (акцій, облігацій) в найбільш вигідній та безпечній пропорції.

Для портфеля з 2-х акцій характерні такі елементи:

• акції А і Б з відповідними номерами 1 та 2;

• норми прибутку та ;

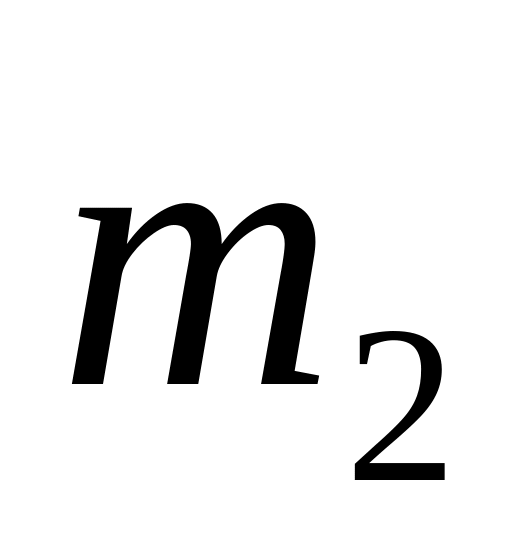• варіації та ;

• середнє квадратичне відхилення та .

Сподівана норма прибутку портфеля з 2-х акцій розраховується за формулою:

, (44)

де та - частки кожної акції в портфелі .

Ризик такого портфеля можна обчислити за допомогою варіації :

, (45)

де - кореляція двох різних видів акцій.

Середнє квадратичне відхилення портфеля з 2-х акцій розраховується за формулою:

(46)

Частки 2-х різних акцій в даному портфелі розраховуються за формулою:

, (47)

а, відповідно, .

Величина кожної з часток акцій залежить від ступеню кореляції між цими акціями ( ). Існує три випадки, коли: =1; =0; =-1. Випадок, коли =1 є одним з екстремальних випадків, який означає абсолютно додатню кореляцію між нормами прибутку 2-х акцій. Він має місце тоді, коли розглядаються акції підприємств, які виготовляють взаємодоповнюючі товари (автомобілі – шини тощо), і норма прибутку однієї акції змінюється прямопропорційно нормі прибутку іншої акції. Випадок абсолютної додатної кореляції не дозволяє досягти істотного ефекту: зменшуючи ризик цих акцій, менеджер зменшує і їх сподівану норму прибутку та навпаки.

Випадок, коли =-1 означає абсолютну від’ємну кореляційну залежність між нормами прибутку 2-х акцій. Величина варіації в даному випадку визначається за формулою:

, (48)

або

Ризик портфеля, виражений як середньоквадратичне відхилення в цьому випадку дорівнюватиме:

(49)

Аналіз рівняння (49) показує, що ризик портфеля в цьому випадку можна суттєво зменшити. Якщо прирівняти до нуля, то

(50)

Тобто, у випадку абсолютної від’ємної кореляції є можливість обрати таку структуру портфеля, який цілком буде позбавлений ризику.

Випадок, коли =0, означає відсутність взаємозв’язку між акціями, тобто формування норми прибутку іншої акції. Величина варіації в даному випадку розраховується за формулою:

(51)

Середньоквадратичне відхилення розраховується за формулою:

(52)

Звідси витікає, що є можливість часткової редукції ризику портфелю 2-х акцій. Частки акцій розраховуються за формулою:

, (53)

або (54)

Перейдемо тепер до загального випадку, коли до складу портфеля залучено багато різних акцій. Вихідна інформація для визначення структури портфеля з багатьох акцій наступна: n – кількість різних акцій, що залучаються до портфеля, пронумерованих від 1 до n; - сподівана норма прибутку і-ої акції (і= ), - коефіцієнт кореляції і-ої та j-ої акції ( ); - частка і-ої акції, залученої до портфеля (і= ).

Очевидно, що (55)

Середня сподівана норма прибутку для портфеля з багатьох акцій розраховується за формулою:

(56)

Величина варіації:

(57)

Середньоквадратичне відхилення:

(58)

З формули (57) витікає, що варіацію, тобто ризик портфеля, можна трактувати як суму двох складових. Перша складова віддзеркалює індивідуальний ризик кожної з акцій, друга складова характеризується взаємозв’язками між парами акцій, тобто показує вплив коефіцієнтів кореляції пар акцій на ризик портфеля: від’ємні величини коефіцієнтів кореляції призводять до зменшення варіації портфеля.

Література: 1, с. 124-164; 9, с. 65-116