1.3. Представление решений в форме бегущих волн

В общем случае решение дифференциальных уравнений (1.3) представляет собой комбинацию так называемых бегущих волн, являющихся функциями времени t и координаты x. Синусоидальный режим линии также характеризуется наличием бегущих волн, структуру которых легко установить, например, на основе соотношений (1.16).

Воспользуемся первым выражением системы (1.16)

(1.21)

и осуществим переход от комплексного значения напряжения к мгновенному. Поскольку выражения в скобках представляют собой комплексные числа, не зависящие от х, то введем обозначения

(1.22)

и представим комплексы составляющих правой части в форме:

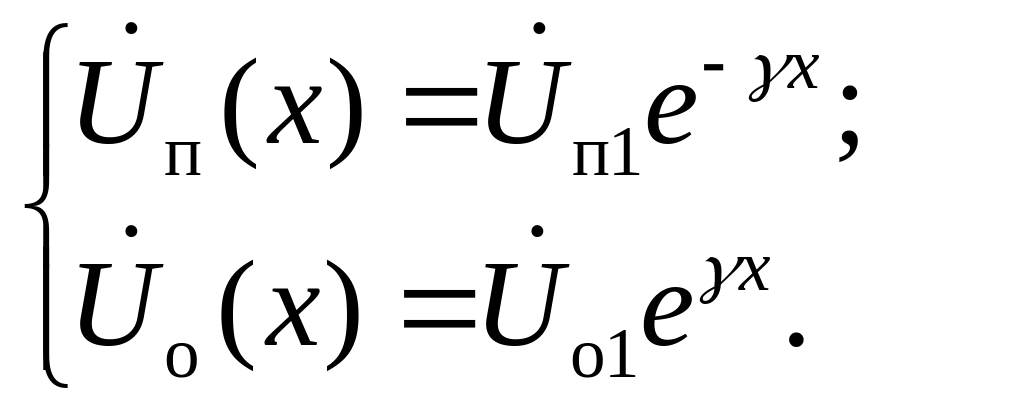(1.23)

Функция описывает так называемую прямую волну напряжения, а – обратную.

Учитывая далее, что согласно расчету по уравнению (1.6) делаем подстановку величин и в выражение (1.21):

(1.24)

и по известным правилам осуществляем переход к мгновенным значениям:

(1.25)

Входящая в формулу (1.25) функция

(1.26)

есть математическое выражение прямой волны, которая является затухающей синусоидой по координате х (рис. 1.6). Степень затухания вдоль линии определяет множитель . Фаза волны при фиксированном моменте времени изменяется на единице длины на величину . Убывание амплитуды волны вдоль линии обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения волны.

В целом распределение (1.26) не является стационарным. С течением времени оно непрерывно перемещается по координате х вдоль линии от начала к концу. Для демонстрации этого явления на рис. 1.6 приведено распределение напряжения для двух моментов времени – t₁ и t₂ (t₂ > t₁).

Рис. 1.6. График распределения прямой волны напряжения для двух моментов времени – t₁ и t₂

Вторая составляющая правой части формулы (1.25)

(1.27)

представляет собой бегущую волну напряжения, перемещающуюся в обратном направлении: от конца линии к ее началу. Эта бегущая волна называется обратной, или отраженной волной (рис. 1.7).

Результирующее синусоидальное напряжение, как следует из формулы (1.25), формируется в виде суммы прямой и обратной волн.

В соответствии с уравнением (1.26) для получения выражения мгновенных значений тока необходимо комплексы прямой и обратной волн разделить на волновое сопротивление и изменить знак второй составляющей. При этом мгновенное значение тока будет иметь вид:

(1.28)

где .

Рис. 1.7. График распределения обратной волны напряжения

Следует обратить внимание на то, что в отличие от напряжения прямая и обратная волны тока не складываются, а вычитаются. Общий характер имеет следующая пара соотношений:

(1.29)

Волны напряжения и тока перемещаются вдоль линии с определенной скоростью. В однородной линии скорость неизменна по всей длине. При анализе синусоидальных процессов линий за скорость движения волны принимают скорость перемещения какой-то фиксированной фазы. Такая скорость называется фазовой.

Фаза функции будет постоянна, если не изменяется ее аргумент Для нахождения фазовой скорости это условие представляется в виде

(1.30)

и выражается производная по времени от обеих частей равенства:

(1.31)

Производная есть скорость, поэтому окончательно

. (1.32)

Вторым параметром бегущих волн является длина волны – расстояние между двумя ближайшими точками, разность фаз колебаний в которых равна Этот параметр определяют выражения:

(1.33)

Параметр , определяемый из выражения (1.6), называется коэффициентом фазы и характеризует изменение фазы напряжения или тока на единицу длины линии.

Фазовая скорость волн напряжения и тока в воздушных линиях близка к скорости распространения электромагнитного поля в воздухе, последняя в чистом воздухе составляет величину

(1.34)

т. е. равна скорости света в вакууме с.

Здесь и – соответственно диэлектрическая и магнитная проницаемость вакуума (воздуха).

В электрических кабелях в основном применяется твердая изоляция из различных диэлектриков. Диэлектрическая проницаемость изоляционных материалов отличается от значения . К примеру, среди других изоляционных материалов широкое применение для кабелей находят различные композиции из полиэтилена. Последний имеет относительную диэлектрическую проницаемость Скорость распространения электромагнитного поля в таком диэлектрике составит величину

(1.35)

что значительно меньше величины Поэтому в кабелях фазовая скорость волн напряжения и тока существенно отличается от скорости волн в воздушных линиях.