1.2. Установившийся синусоидальный режим линии

В установившемся синусоидальном режиме линии решение дифференциальных уравнений (1.3) проводится для комплексов напряжения и тока . Последние не являются функциями времени, поэтому задача сводится к решению обыкновенных дифференциальных уравнений с постоянными коэффициентами. Действительно, подстановка и в уравнения (1.3) вместо мгновенных значений u и i приводит к уравнениям:

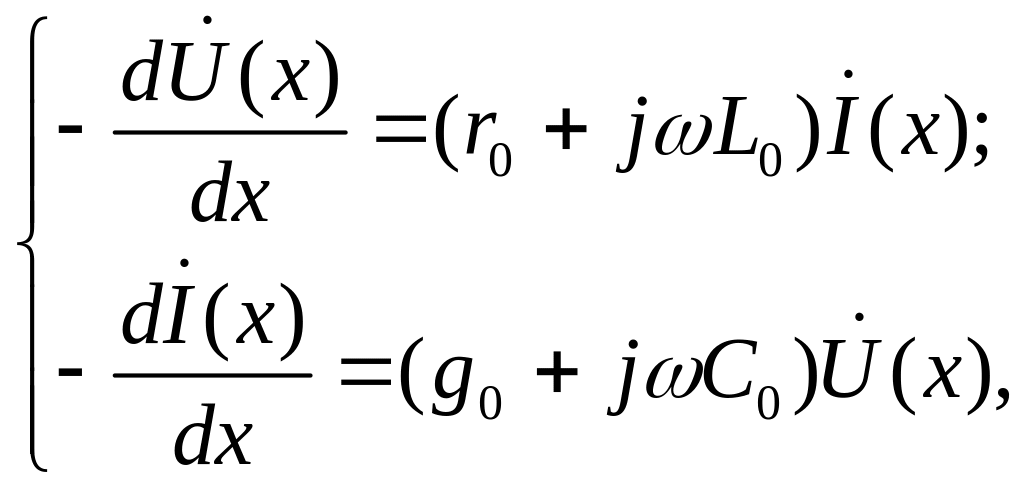(1.4)

которые в результате простейших преобразований сводятся к двум уравнениям второго порядка относительно и :

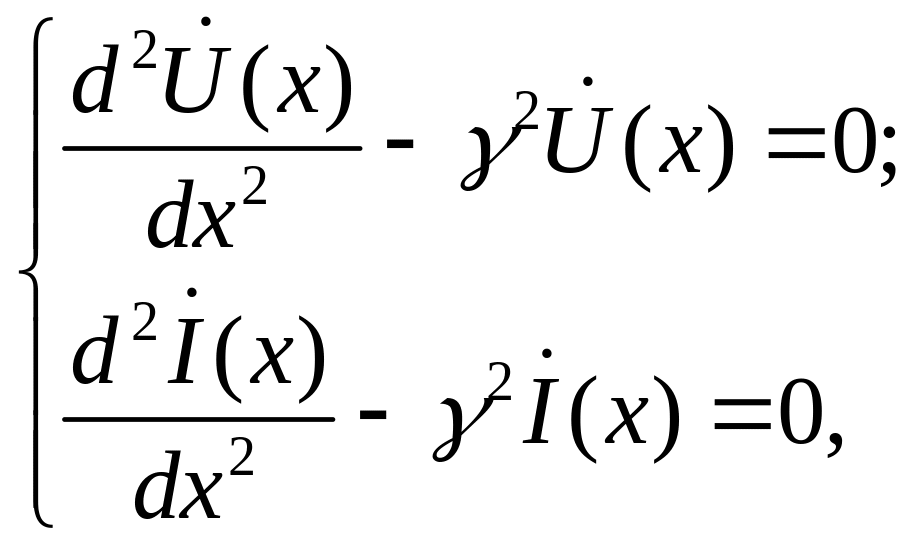(1.5)

известным как уравнения Гельмгольца. Здесь

– (1.6)

комплексное число, называемое коэффициентом распространения, 1/км.

Каждому из уравнений (1.5) соответствует характеристическое уравнение

, (1.7)

имеющее корни .

Для напряжения решение имеет вид:

, (1.8)

где А₁ и А₂ – неизвестные постоянные.

Чтобы получить решение для тока, используем первое уравнение системы (1.4), которое после подстановки выражения (1.8) дает:

(1.9)

откуда

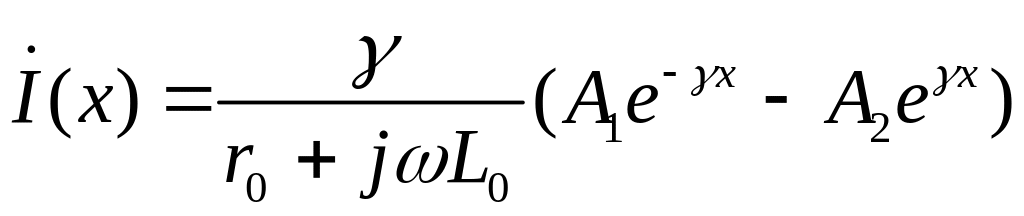(1.10)

или

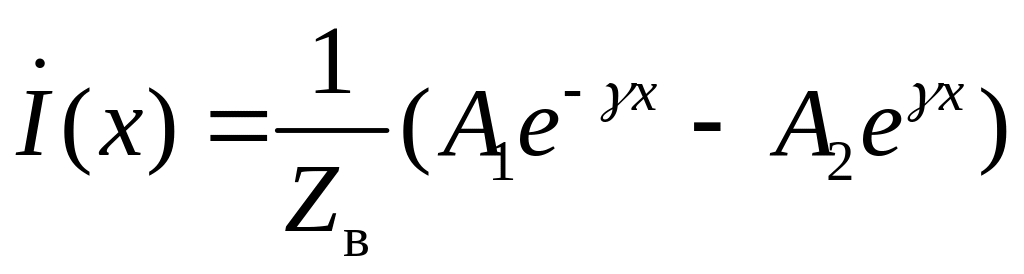, (1.11)

где – величина, называемая волновым сопротивлением,

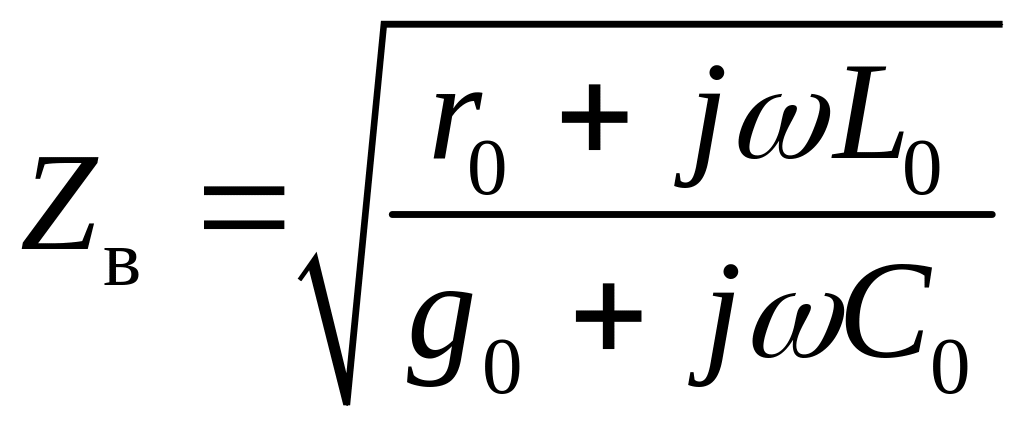. (1.12)

В итоге формулы (1.8) и (1.11) образуют систему уравнений с неизвестными коэффициентами А₁ и А₂:

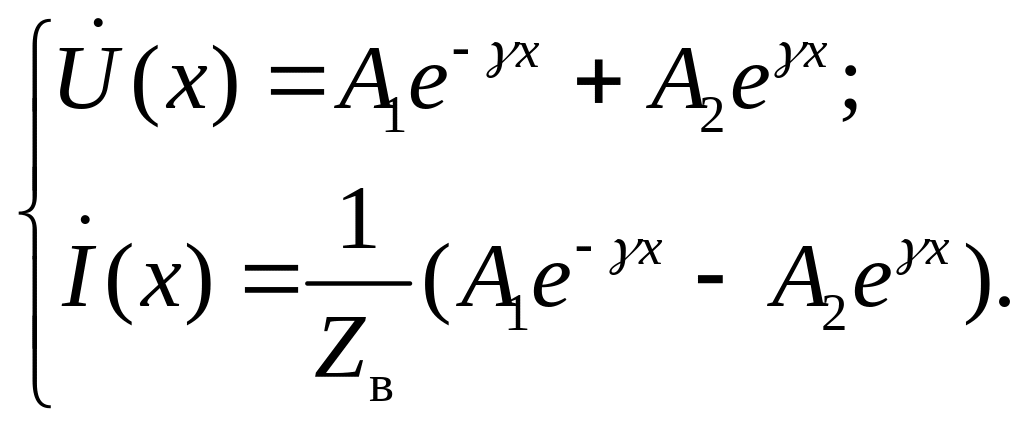(1.13)

Определение А₁ и А₂ осуществляется по известным или заданным граничным значениям напряжения и тока.

Условимся обозначать через и комплексы напряжения и тока в начале линии, а через и – в конце ее (рис. 1.5).

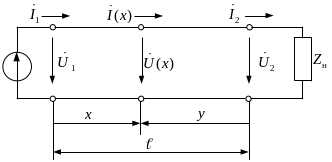
Рис. 1.5. Схема для определения расчетных уравнений линии с распределенными параметрами

Если заданы и , то система (1.13) записывается при х = 0:

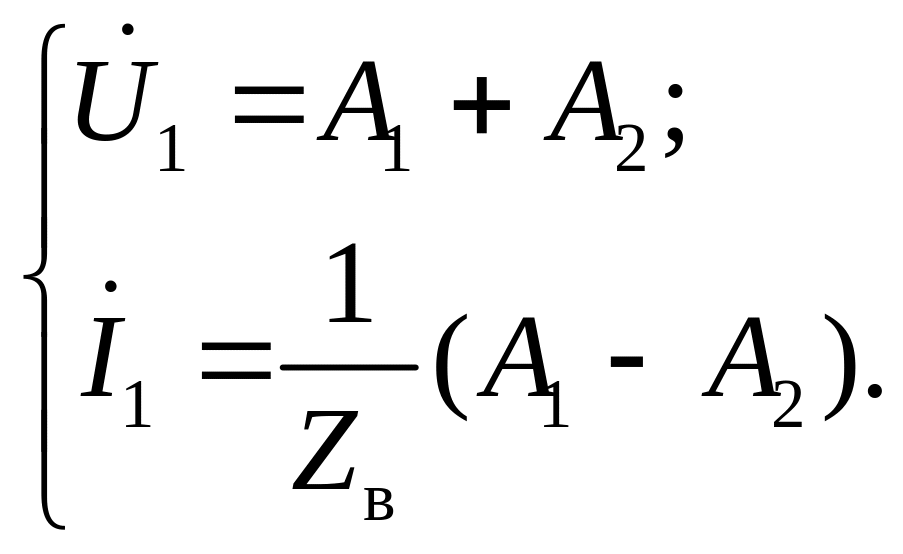(1.14)

Решение системы (1.14) дает значения постоянных:

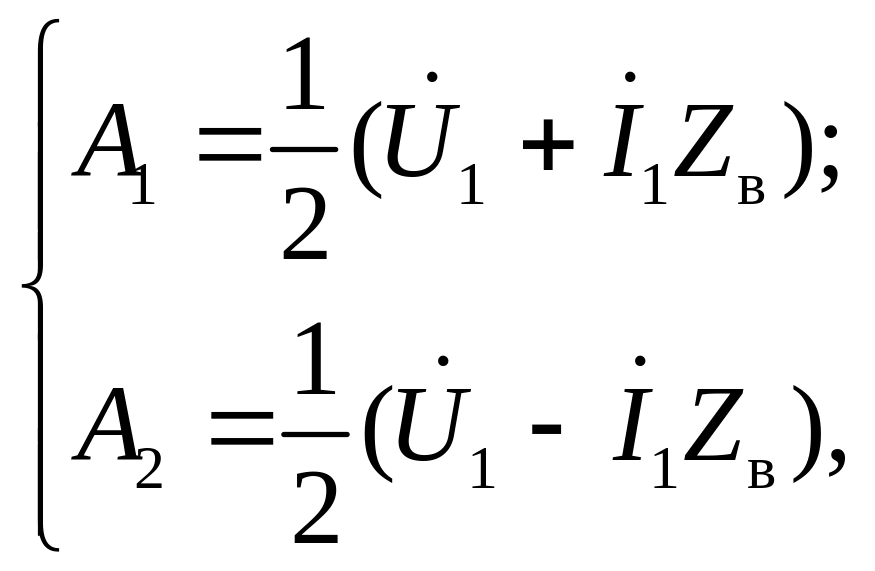(1.15)

подстановка которых в систему (1.13) приводит к соотношениям:

(1.16)

Полученные выражения позволяют определить комплексы напряжения и тока и в любой точке линии по значениям и в начале линии. Координата х в этом случае отсчитывается от начала линии.

При известных параметрах и координата y отсчитывается от конца линии. Для получения расчетных соотношений достаточно величины и в системе (1.16) заменить на и , а переменную х – соответственно на ℓ – x = = y. В результате получим:

(1.17)

Выражения (1.17) позволяют определить напряжение и ток в любой точке линии по известным величинам и в конце линии.

В расчетах используются и другие формы соотношений. Так, преоб­разование (1.16) с учетом известных соотношений для гиперболических функций

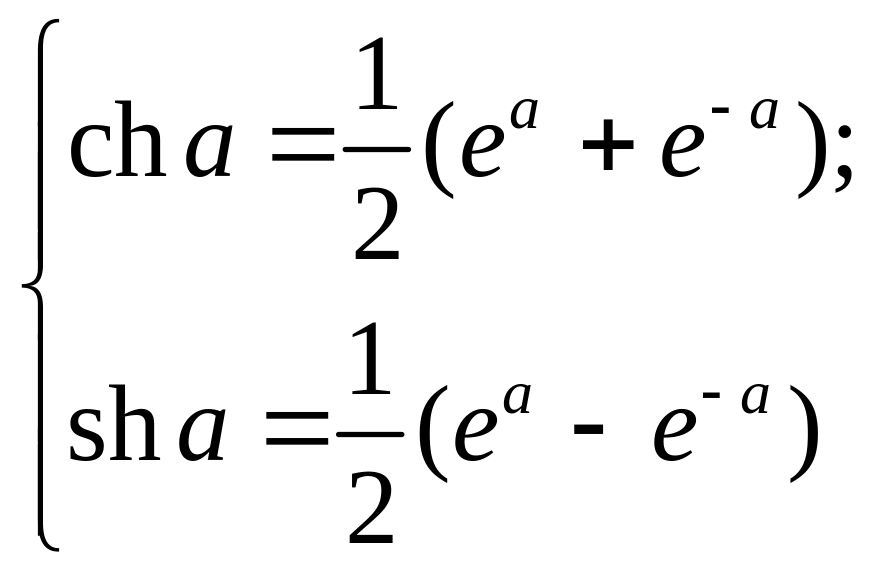(1.18)

приводит к выражениям:

(1.19)

Точно так же из уравнений (1.17) выводится пара соотношений:

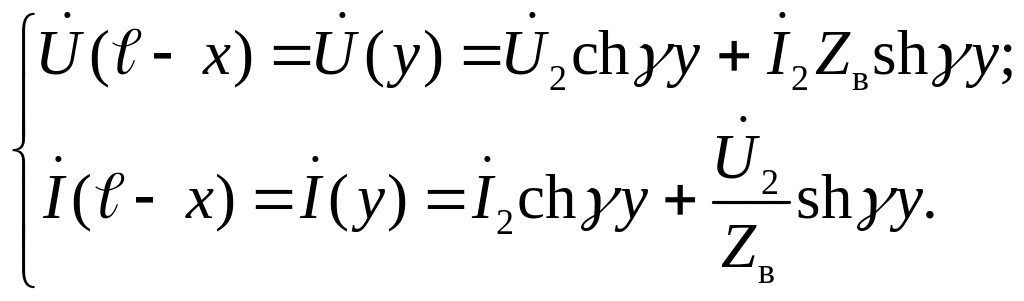(1.20)

Переменная y в выражениях (1.17) и (1.20) отсчитывается от конца линии.

Соотношения (1.16), (1.17), (1.19) и (1.20) получены в предположении, что линия является линейной электрической цепью. Для такой цепи применим принцип наложения, поэтому указанные соотношения могут быть использованы для расчета несинусоидальных режимов, когда токи и напряжения содержат кроме основной еще и высшие гармоники. В этом случае расчет ведется отдельно для каждой гармоники.