2.6. Неискажающая линия

Смысл понятия неискажающей линии можно раскрыть для случая, ког- да на входе линии действует несинусоидальное напряжение, описываемое рядом Фурье.

Условие задачи. Линия длиной 50 км имеет следующие первичные параметры:

На входе линии действует несинусоидальное периодическое напряжение Частота первой гармоники f = 800 Гц. Требуется с помощью расчета убедиться в том, что при переходе к неискажающей линии исчезает зависимость от частоты волнового сопротивления Z_в, коэффициента затухания α, фазовой скорости V_ф, а коэффициент фазы β становится линейной функцией частоты. Определить напряжение u₂ и ток i₂ в конце линии.

Порядок расчета. Входное напряжение содержит нулевую, первую и третью гармоники, поэтому номер гармоники k принимает значения 0, 1, 3.

Волновые сопротивления гармоник:

при k = 0 –

k = 1 –

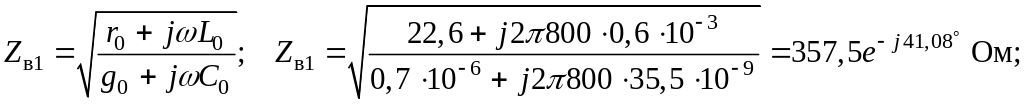
k = 3 –

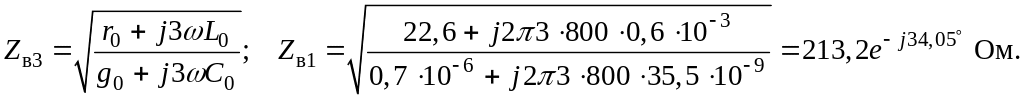
Коэффициент распространения:

при k = 0 –

k = 1 –

k = 3 –

Фазовая скорость:

при k = 1 –

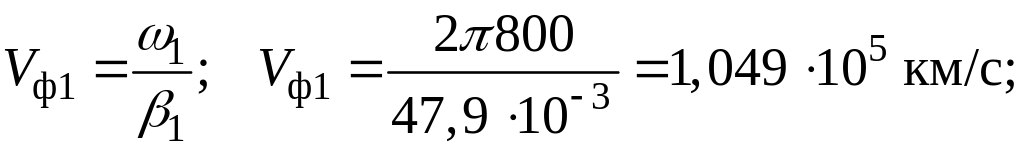
k = 3 –

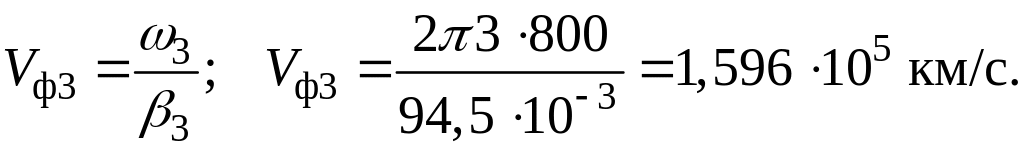
По полученным результатам легко убедиться в том, что рассмотренные параметры зависят от номера гармоники k, т. е. от частоты. Несовпадение значений фазовых скоростей гармоник и указывает на нелинейный характер зависимости коэффициента фазы от частоты.

Используем далее условие неискажающей передачи (1.71) и находим удовлетворяющее этому условию значение индуктивности:

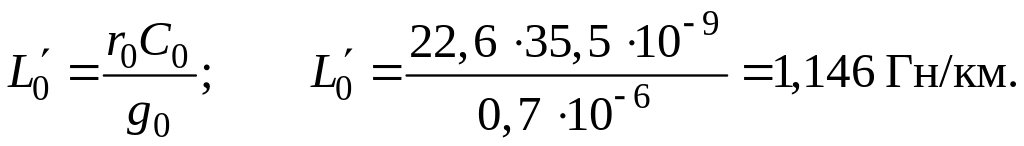
Волновое сопротивление неискажающей линии согласно формуле (1.72) можно рассчитать по уравнению:

Требование отсутствия искажений передаваемых сигналов предполагает, что неискажающая линия находится в режиме согласованной нагрузки:

Индекс k означает, что данная величина справедлива для каждой гар­моники.

Коэффициент затухания определяется по выражению (1.74):

Фазовая скорость – по формуле (1.75):

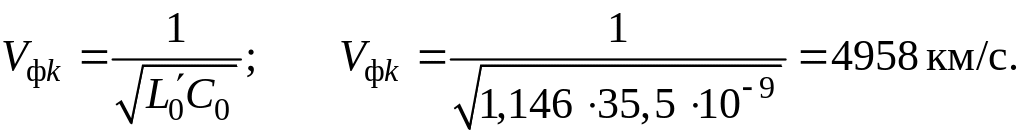
Величина V_фk так же, как α_k, не зависит от частоты.

Коэффициент фазы как линейная функция от частоты рассчитывается по формуле (1.74):

Так как неискажающая линия находится в режиме согласованной нагрузки, гармоники напряжения в конце линии можно выразить из системы уравне- ний (1.67):

при k = 0 –

k = 1 –

k = 3 –

Напряжение в конце линии

Ток в конце линии

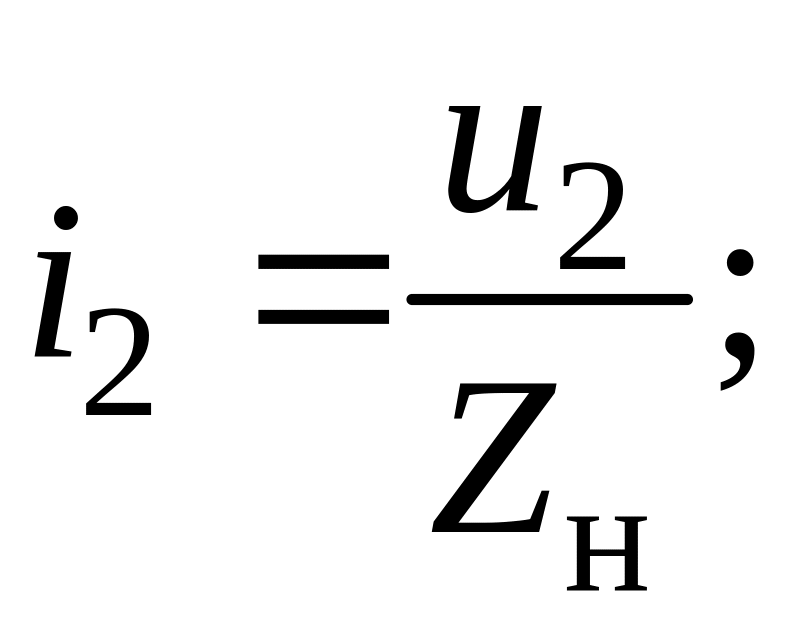
Напряжение u₂ имеет ту же форму, что и u₁, поскольку при выполнении условия независимости коэффициента затухания α от частоты все составляющие напряжения u₁ при переходе к u₂ изменились в одинаковое количество раз. Равенство фазовых скоростей гармоник исключило дисперсию волн, т. е. еще один фактор искажения, обусловленный разными фазовыми скоростями гармони­ческих составляющих. Наконец, обеспечение линейного закона изменения коэффициента β от частоты обусловило отсутствие фазовых искажений.

На рис. 2.2, а в одинаковых масштабах приведены кривые входного и выходного напряжений u₁ и u₂ для случая, когда выполняются условия неискажающей передачи сигналов ( ; ). На оси времени отмечены точки, кратные четверти периода несинусоидальной функции . Из графика на рис. 2.2, а видно, что форма напряжений u₁ и u₂ одинакова. На рис. 2.2, б – г для сравнения в том же масштабе изображены кривые для произвольных нагрузок: б – активно-емкостная нагрузка (r_н = 600 Ом; C_н = 3,3·10^–7 Ф); в – активно-индуктивная нагрузка (r_н = = 600 Ом; ); г – индуктивная нагрузка ( ).

Рис. 2.2. Входное и выходное напряжения u₁ и u₂ для различных нагрузок

Линия, для которой проводился расчет, имеет достаточно высокое затухание, что видно из значений коэффициента затухания α_k на частотах гармоник: , , Поэтому напряжение u₂ (см. рис. 2.2, б – г) имеет по сравнению с u₁ малые значения амплитуды и существенно отличаются по форме. Здесь сказывается влияние длины линии (ℓ = 50 км), которая для заданных в рассматриваемом примере первичных параметров является весьма значительной.

Коэффициент затухания α_k неискажающей модели линии ( ), как показал расчет, одинаков для всех гармоник и на порядок меньше приведенных выше исходных значений α₁ и α₃. Поэтому напряжение u₂ на рис. 2.2, а, в отличие от рис. 2.2, б – г, в меньшей степени отличается по амплитуде от напряжения u₁.

Индуктивность L₀ – единственный параметр, которым можно варьировать в сторону увеличения. Однако реализация условия (1.71) путем увеличения L₀ на практике затруднительна. Кроме того, увеличение индуктивности приводит к нежелательному уменьшению фазовой скорости и, соответственно, к увеличению времени прохождения электрического сигнала по линии.