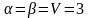Г) Одноканальная смо с (неограниченным) ожиданием.

Проанализируем работу одноканальной СМО с ожиданием без ограничений на длину очереди и на время ожидания в очереди. По-прежнему будем предполагать, что входящий поток и поток обслуживаний являются простейшими и имеют интенсивности λ и μ соответственно.

Такая система представляет собой предельный случай системы, рассмотренной в предыдущем пункте, при m →∞ . Таким образом, длина очереди станет бесконечной и в соответствии с этим бесконечным станет число состояний СМО. Размеченный граф состояний представлен на рис. 11.

Если отказаться от ограничения на длину очереди, то случаи ρ<1 и ρ≥1 начинают существенно различаться.

Если λ>μ (ρ>1), т.е. среднее число заявок, поступивших в систему за единицу времени, больше среднего числа обслуживаемых заявок за то же время при непрерывно работающем канале, то очевидно, что очередь неограниченно растет. В этом случае предельный режим не устанавливается и предельных вероятностей состояний не существует (точнее, они равны нулю).

В случае λ=μ (ρ=1) только при условии, что входящий поток заявок и поток обслуживаний регулярные (т.е. заявки поступают в СМО через равные интервалы времени, и время обслуживания одной заявки является постоянным, равным интервалу времени между поступлениями заявок), очереди вообще не будет, и канал будет обслуживать заявки непрерывно. Но как только входящий поток или поток обслуживаний перестает быть регулярным и приобретает элементы случайности, очередь начинает расти до бесконечности.

Поэтому далее при рассмотрении указанных систем будем предполагать, что λ<μ, т.е. ρ<1. При этом условии с течением времени устанавливается предельный режим, и предельные вероятности состояний существуют.

Устремляя m к бесконечности в формулах для вероятностей состояний (полученных для СМО с ограниченной длиной очереди при ρ<1), находим выражения для предельных вероятностей состояний рассматриваемой СМО:

При отсутствии ограничений на очередь каждая заявка, поступившая в СМО, рано или поздно будет обслужена. Поэтому вероятность отказа равна нулю: Pотк=0 .

Следовательно, вероятность того, что поступившая заявка будет принята в систему, так же как и относительная пропускная способность Q , равна единице:

Q =1−Pотк =1 .

Тогда для абсолютной пропускной способности A (и интенсивности выходящего потока) будем иметь: A = λ*Q =λ, т.е. интенсивности входящего и выходящего потоков совпадают.

Среднее число заявок в очереди L оч :

Среднее время ожидания заявки в очереди по формуле Литтла равно

Наконец, среднее время пребывания заявки в СМО TСМО складывается из среднего времени заявки в очереди T оч и среднего времени обслуживания заявки T об:

6. Теория игр. Нижняя и верхняя цены игры. Принцип минимакса

Итак, рассмотрим матричную игру с платежной матрицей

(1.2)

Где i-я строка соответствует А_i-й стратегии игрока А;

j-й столбец соответствует В_j-й стратегии игрока В.

Пусть игрок А выбирает некоторую стратегию А_i, тогда в наихудшем случае (например, если выбор станет известен игроку В) он получит выигрыш равный . Предвидя эту возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный в каждой стратегии выигрыш . Таким образом, . Величина называется нижней ценой игры ( – это гарантированный выигрыш игрока А).

Очевидно, находится в одной из строк матрицы Н, пусть в i₀, тогда стратегия называется максиминной.

Итак, если игрок А будет придерживаться максиминной стратегии, то ему при любом поведении игрока В гарантируется выигрыш, во всяком случае не меньше .

С другой стороны, противник – игрок В, заинтересован в том, чтобы обратить выигрыш игрока А в минимум, поэтому он должен пересмотреть каждую свою стратегию с точки зрения максимального выигрыша игроком А при этой стратегии. Другими словами, при выборе некоторой стратегии B_j он должен исходить из максимального проигрыша в этой стратегии, равного , и найти такую стратегию, при которой этот проигрыш будет наименьшим, то есть не более чем .

Величина называется верхней ценой игры, а соответствующая ему стратегия – минимаксной.

Принцип осторожности, диктующий игрокам выбор стратегий максиминной или минимаксной соответственно, в теории игр именуют принципом минимакса, а сами стратеги максиминные и минимаксные – общим термином минимаксные стратегии.

Рассмотрим пример нахождения и .

Пример

Пусть игра задана матрицей

Определим нижнюю и верхнюю цены игры.

Выпишем для каждой строки справа от матрицы , а снизу каждого столбца. Тогда получим:

В этом примере нижняя и верхняя цены игры совпадают: