5. Выборочное наблюдение
Формулы для средней ошибки выборки:
в случае повторного отбора:
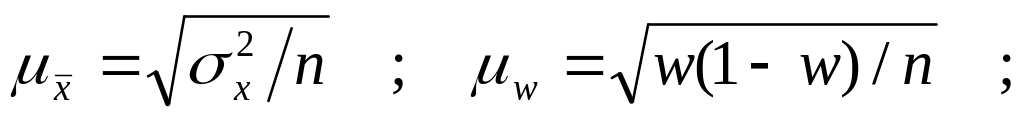
в случае бесповторного отбора:
Соответствие значений t и доверительных вероятностей Р:
t |
1,0 |
1,5 |
1,64 |
2,0 |
2,5 |
3,0 |
3,5 |
Р |
0,683 |
0,866 |
0,95 |
0,954 |
0,988 |
0,997 |
0,999 |
Задача 5.1. На машиностроительных заводах области работает 25000 рабочих. В порядке случайной бесповторной выборки обследовано 4900 рабочих. На основе этого обследования установлено: а) среднемесячная з/плата – 2900 руб.; б) среднее квадратическое отклонение – 365 руб. Определить среднюю ошибку выборки и возможные пределы средней заработной платы с вероятностью 0,954.
Задача 5.2. Как изменится средняя ошибка выборки при обследовании рабочих с целью определения средней з/платы, если при неизменных объеме выборки и дисперсии з/платы доля обследованных рабочих уменьшится с 36% до 19%?
Задача 5.3. При 20%-м выборочном обследовании (по способу случайной бесповторной выборки) населения города с численностью 380000 чел установлено: удельный вес населения в возрасте до 16 лет составил 14%. Определить с вероятностью 0,95 пределы, в которых будет находиться доля этой группы населения.
Задача 5.4. Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5%-я механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования кредитом – 30 дней при среднем квадратическом отклонении 9 дней. В пяти счетах (из 100) срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определить пределы, в которых будут находиться срок пользования краткосрочным кредитом в банке и доля счетов со сроком пользования более 60 дней.
Задача 5.5. С целью прогнозирования урожая пшеницы в хозяйстве была произведена 10%-я выборка, в которую попали три участка. Урожайность на этих участках составила: 20, 25 и 21 ц/га. С вероятностью 0,95 определить пределы, в которых будет находиться средняя урожайность пшеницы в этом хозяйстве.
Задача 5.6. Из 12000 сотрудников коммерческих банков области с целью определения доли сотрудников в возрасте старше 40 лет было обследовано 500 человек, из которых старше 40 лет оказалось 175 человек. С вероятностью 0,997 определить долю сотрудников данного возраста в общей численности работников банков.
Задача 5.7. В городе А с целью определения средней продолжительности поездки населения на работу предполагается провести выборочное обследование методом случайного отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,95 (0,997) ошибка выборочной средней не превышала 5 мин. при среднем квадратическом отклонении 20 мин.?
Задача 5.8. В городе В с числом семей 10000 предполагается методом случайного бесповторного отбора определить долю семей с детьми школьного возраста. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,03, если дисперсия равна 0,24?
Задача 5.9. Средняя списочная численность рабочих на заводе 5000 чел. По данным 1%-го выборочного обследования их свободного времени получено, что оно составляет в среднем 6,2 часа в день при средней ошибке выборки 1,2 часа. Какова должна быть численность обследованных рабочих, чтобы ошибка выборки уменьшилась в два раза?