3. Асимптоти гіперболи.

Прямі, рівняння яких ,називаються асимптотами гіперболи.

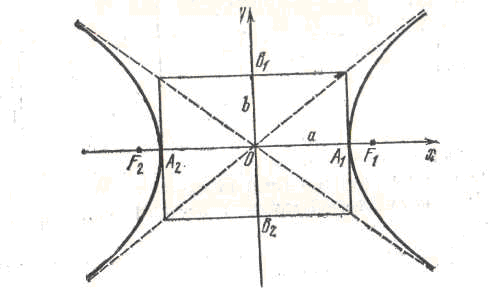
Асимптоти гіперболи є продовженнями діагоналей прямокутника, сторони якого паралельні осям Ох і Оу і дорівнюють відповідно 2а і 2y, а його центр знаходиться всередині вертикальних кутів, що утворені асимптотами, і наближаються як завгодно близько до асимптот.

Гіпербола складається із двох не зв’язаних між собою частин, які називається її вітками.

4. Ексцентриситет гіперболи.

Ексцентриситетом гіперболи називається відношення півфокусної відстані до дійсної півосі і позначається >1.

Меншим значенням відношення відповідають менші значення ексцентриситету. Таким чином, чим менше ексцентриситет гіперболи, тим сильніше стиснена вона до осі абсцис.

5. Спряжена гіпербола.

Дві гіперболи, які визначаються рівняннями і в одній і тій же системі координат і при тих самих значеннях а і b, називаються спряженими одна до одної.

6. Рівностороння гіпербола.

Гіпербола називається рівносторонньою, якщо довжини її півосей рівні між собою. Оскільки для рівносторонньої гіперболи , то її рівняння має вигляд або . Рівностороння гіпербола визначається одним параметром і асимптотами являються бісектриси координатних кутів .

У всіх рівносторонніх гіпербол один і той самий ексцентриситет .

Так як асимптоти рівносторонньої гіперболи взаємно перпендикулярні, їх можна прийняти за осі нової системи координат, отриманої в результаті повороту осей старої системи навколо початку координат на кут .

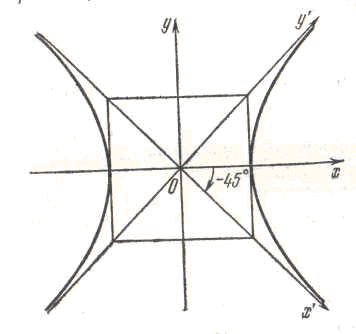
Рівняння рівносторонньої гіперболи, віднесеної до своїх асимптот: .

Якщо, центр гіперболи знаходиться не в початку координат, а в точці , а осі гіперболи паралельні осям координат, то рівняння гіперболи буде мати вигляд або - рівняння гіпербол зі зміщеним центром.

7. Канонічне рівняння параболи.

Параболою називається множина точок площини, для кожної з яких відстань до даної точки дорівнює відстані до даної прямої, яка не проходить через дану точку.

Така точка називається фокусом параболи, а пряма – директрисою.

Відстань від фокуса до директриси називається фокальним параметром параболи і позначається через р.

Виберемо систему координат таким чином. Вісь Ох проведено через фокус F перпендикулярно до директриси. Точку перетину осі абсцис з директрисою позначимо через К, за початок координат візьмемо середину О відрізка FK, за додатній напрям осі Ох – напрям променя ОF.

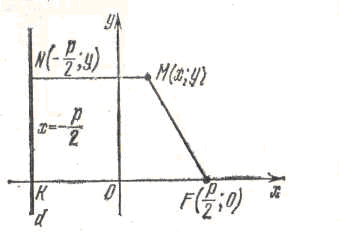
У цій системі координат фокус F має координати , а рівнянням директриси є рівняння .

Нехай - будь-яка точка шуканої множини. Опустимо із точки М перпендикуляр на директрису, і нехай N – основа цього перпендикуляра. Тоді є відстань від точки М до директриси і, отже , оскільки , , то . Це рівняння є рівнянням параболи у вибраній системі координат. Його можна спростити, внаслідок того що обидві частини рівняння невід’ємні, то рівняння рівносильне рівнянню .

В результаті перетворень дістанемо рівняння . Це рівняння називається канонічним рівнянням параболи.