9 Алгоритм определения производной элементарной функции

Что то не то тут…. Наверное это в лекциях есть

Путь x – аргумент функции f(x) и   - малое число, отличное от нуля.  (читается «дельта икс») называют приращением аргумента функции. На рисунке красной линией показано изменение аргумента от значения x до значения   (отсюда видна суть названия «приращение» аргумента). При переходе от значения аргумента   к   значения функции изменяются соответственно от   до   при условии монотонности функции на отрезке  . Разность  называют приращением функции f(x), соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.   Рассмотрим эти понятия на конкретном примере. Возьмем, к примеру, функцию  . Зафиксируем точку   и приращение аргумента  . В этом случае приращение функции при переходе от   к   будет равно   Отрицательное приращение   говорит об убывании функции на отрезке  . Графическая иллюстрация Определение производной функции в точке. Пусть функция f(x) определена на промежутке (a; b),   и   - точки этого промежутка. Производной функции f(x) в точке   называется предел отношения приращения функции к приращению аргумента при  . Обозначается  . 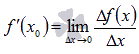Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, что производная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует. Функцию f(x) называют дифференцируемой в точке  , когда она имеет в ней конечную производную. Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке  , то есть, мы имеем возможность определить новую функцию  , которую называют производной функции f(x) на интервале (a; b). Операция нахождения производной называется дифференцированием. Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция. Давайте разберем это на примерах для ясности картины. При дифференцировании будем пользоваться определением производной, то есть переходить к нахождению пределов. При возникновении трудностей рекомендуем обращаться к разделу теории пределы, основные определения, примеры нахождения, задачи и подробные решения. 

10 Предел деференцирования

Правила дифференцирования

Производная постоянной равна нулю.

.

В самом деле, пусть  ,  . Тогда для любой точки    . Поэтому     и  , т.е.  .

Производная суммы, произведения и частного дифференцированных функций.

,  ,  ;   – фиксированная точка;

  

  .

Заметим сразу, что обратные утверждения не верны, т.е.,  например, из существования производной суммы двух функций не следует существование производных слагаемых.

Контрпример. Пусть  ,  . Тогда   – существует для любого  . Но можно взять   и   и тогда слагаемые функции – не дифференцируемые на  , поскольку при   их производные не существуют.

Доказательство. 1. Пусть . Тогда

.

Применяем теорему о пределе суммы, получаем

,

т.е. производная суммы двух дифференцируемых функций существует и равна сумме производных слагаемых функций.

Впредь формулы для простоты будем записывать, опуская  аргумент, т.е. в виде  .

Утверждение может быть обобщено на любое конечное множество слагаемых дифференцируемых функций.

2. Аналогично для   имеем

.

Поэтому  

. Здесь применяем теорему о пределе суммы и произведения функций, а также теорему о непрерывности дифференцируемой функции. Итак,

.

Частные случаи:  ;

, здесь   – третья дифференцируемая в точке   функция.

3. Для  ,    на  , рассуждения проводятся аналогично. Рекомендуем провести их самостоятельно.

Частные случаи:  ;  .

Дифференцируемость сложной функции.

Если  1)  ,   – дифференцируемая в точке   функция для    ; 2)  ,   – дифференци-руемая в точке   функция, то сложная функция  ,   – дифференцируемая функция в точке  , причем

  при  ,  .

Доказательство. Используя дифференцируемость компонент, покажем дифференцируемость сложной функции через существование ее производной в точке. Пусть   – фиксированная точка,  ,   – произвольное приращение независимого переменного  ,  . Тогда

;

  (считаем  ). Тогда существует  . Здесь используется теорема о пределе произведения функций, а также свойство непрерывности дифференцируемой функции:  .

Итак, производная сложной функции   в точке   существует и по теореме о необходимом и достаточном условии дифференцируемости   дифференцируема в точке  , причем

.