
- •Термодинамика и теплопередача. Учебное пособие
- •Раздел I. Техническая термодинамика
- •Содержание
- •Раздел I
- •Тема 1. Газ, как рабочее тело термодинамических систем
- •Тема 2. Первый закон термодинамики
- •Тема 3. Термодинамические процессы
- •Тема 4. Второй закон термодинамики
- •Тема 5. Идеальные циклы тепловых двигателей
- •Основные условные обозначения
- •Основные сечения потока
- •Сокращения
- •Используемые индексы
- •Предисловие
- •Введение
- •Раздел I техническая термодинамика
- •Тема 1. Газ, как рабочее тело термодинамических систем
- •1.1. Структура основных понятий термодинамики авиационных гтд
- •1.2. Основные понятия и определения термодинамики
- •1.3. Реальный и идеальный газы. Параметры состояния рабочего тела
- •1.3.1. Давление
- •1.3.2. Температура
- •1.3.3. Удельный объём, плотность
- •1.4. Уравнение состояния идеального и реального газов
- •1.4.1. Уравнение состояния идеального газа
- •1.4.2. Уравнение состояния реального газа
- •1.5. Понятие о термодинамическом процессе. Равновесные (обратимые) и неравновесные (необратимые) процессы
- •1.5.1. Равновесные (обратимые) процессы
- •1.5.2. Графическое изображение термодинамического процесса
- •1.5.3. Неравновесные (необратимые) процессы
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 2. Первый закон термодинамики
- •2.1. Внутренняя энергия рабочего тела. Изменение внутренней энергии
- •2.2. Работа газа, как форма передачи энергии в термодинамическом процессе
- •2.3. Теплота, как форма передачи энергии в термодинамическом процессе
- •2.4. Энтропия. Энтропийная “t-s” диаграмма
- •2.5. Зависимость количества работы и теплоты от характера термодинамического процесса
- •2.6. Теплоёмкость газа. Уравнение Майера. Показатель адиабаты
- •2.7. Энтальпия
- •2.8. Техническая работа (работа движущегося газа)
- •2.9. Содержание и уравнение первого закона термодинамики
- •2.10. Чистые вещества и смеси газов
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 3. Термодинамические процессы
- •3.1. Последовательность и объём расчёта термодинамических процессов
- •3.2. Изохорный процесс: определение, осуществление и исследование
- •3.2.1. Исследование изохорного процесса
- •3.3. Изобарный процесс: определение, осуществление и исследование
- •3.3.1. Исследование изобарного процесса
- •3.4. Изотермический процесс: определение, осуществление, исследование
- •3.4.1. Исследование изотермического процесса
- •3.5. Адиабатный (изоэнтропический) процесс: определение, осуществление, исследование
- •3.5.1. Исследование адиабатного процесса
- •3.6. Сравнение адиабаты и изотермы
- •3.7. Обобщающее значение политропных процессов
- •3.8. Энтальпийная “I-s” диаграмма (“I-s” координаты)
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 4. Второй закон термодинамики
- •4.1. Понятие о круговых процессах (циклах). Прямой цикл (цикл тепловой машины)
- •4.2. Полезная работа цикла. Термический кпд цикла
- •4.3. Цикл Карно и теорема Карно
- •4.4. Обратные циклы (циклы холодильных машин)
- •4.5. Второй закон термодинамики. Формулировки второго закона термодинамики
- •4.6. Второй закон термодинамики и энтропия
- •4.7. Статистическая интерпретация второго закона термодинамики
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Информация к размышлению
- •Проверьте, как Вы усвоили материал
- •Тема 5. Идеальные циклы тепловых двигателей
- •5.1. Особенности термодинамического метода исследования циклов тепловых двигателей
- •5.2. Схема устройства и принцип работы авиационного газотурбинного двигателя (гтд)
- •5.3. Идеальный цикл гтд (цикл Брайтона – Стечкина)
- •5.4. Работа и термический кпд цикла гтд
- •5.6. Сравнение циклов Брайтона и Гемфри
- •5.7. Цикл с регенерацией тепла
- •5.8. Цикл со ступенчатым подводом тепла
- •5.9. Эксергетический метод термодинамического анализа
- •5.10. Идеальные циклы двигателей внутреннего сгорания (двс)
- •5.10.1. Идеальный цикл двс с подводом тепла
- •5.10.2. Идеальный цикл двс с подводом тепла при постоянном
- •5.10.3. Сравнение циклов Отто и Дизеля
- •5.10.4. Цикл двс со смешанным теплоподводом
- •Примеры решения задач
- •Решение
- •Решение
- •4. Эффективность цикла оцениваем по величине термического кпд цикла
- •Решение
- •Проверьте, как Вы усвоили материал
- •Заключение
- •Список использованной литературы
- •Приложение
- •Международная стандартная атмосфера (мса) гост 4401–81 (фрагмент)
- •Теплофизические величины
- •Соблюдайте гост 8.417 – 2002
1.3.3. Удельный объём, плотность
Удельный объём υ – объём занимаемый 1 кг рабочего тела (газа) и определяется по формуле:
υ = V/m, м3/кг, (1.6)
где V – объём занимаемый газом м3;
m – масса газа, кг.
Плотностью ρ называется количество газа, заключённое в единице объёма. Следовательно, если m кг занимают объём V м3, то плотность его определяется по формуле
ρ = m/V, кг/м3. (1.7)
Из данных определений видно, что плотность газа ρ это величина обратная удельному объёму υ, т.е.
ρ·υ = 1. (1.8)
1.4. Уравнение состояния идеального и реального газов
1.4.1. Уравнение состояния идеального газа
Основные параметры рабочего тела независимо от его агрегатного состояния связаны между собой уравнением, называемым уравнением состояния, которое может быть представлено так:
f (p, υ, T) = 0. (1.9)
Уравнение (1.9) в пространстве отображает поверхность, которая характеризует всевозможные равновесные состояния химически однородной термодинамической системы (газ, жидкость). При отсутствии внешних полей (гравитационного, электрического, магнитного) число независимых параметров, однозначно определяющих равновесное состояние системы, будет равно двум из трех (p, υ, T), так как любой из этих трех параметров является однозначной функцией двух заданных.
Например, если принять за независимые переменные υ и T, то p можно выразить как функцию υ и Т, т.е. р = р (Т, υ); если же за независимые переменные принять р и Т, то удельный объём можно выразить как функцию р и Т, т.е. υ = υ (р, Т).
Таким образом, уравнение состояния устанавливает связь между давлением, температурой и удельным объёмом однородной термодинамической системы.
Наиболее простой вид уравнение состояния имеет для идеальных газов. Свойства идеальных газов, как известно, основаны на экспериментальных законах. (Законы Бойля – Мариотта, Гей – Люсака и Шарля).
Эти законы можно объединить в один, который формируется так: для данного газа произведение давления на объём в любом состоянии пропорционально его массе и абсолютной температуре.
Математическая запись этого закона выражается уравнением Клапейрона (1834 г.).
p·V = m·R·T (1.10)
Для одного кг газа уравнение (1.10) принимает вид:
p·υ = R·T (1.11)
В уравнениях (1.10), (1.11) коэффициент R имеет размерность Дж/(кг·K) и называется газовой постоянной, которая зависит от молекулярной массы газа μ.
Уравнению Клапейрона можно придать универсальную форму, если отнести газовую постоянную к одному киломолю газа.
Киломолем (кмоль) или килограммолекулой называется количество килограммов вещества, численно равное его молекулярной массе.
Обе части уравнения (1.11) умножим на массу одного киломоля μ, г/кмоль.
p·υ·μ = R·T·μ , (1.12)
где
υ·μ
= Vμ
,
![]() –
объём
одного киломоля газа;
–
объём
одного киломоля газа;
μ·R = Rμ , Дж/(кмоль·К) – универсальная газовая постоянная.
Известно, что идеальные газы подчиняются закону Авогадро (1811 г.), который гласит, что при одинаковых температурах и давлениях объёмы, занимаемые одним киломолем любого идеального газа, одинаковы. Измерения показали, что при нормальных атмосферных условиях (pо = 101325 Па; То = 273,15 К) один киломоль идеального газа занимает Vμ = 22,4136 м3, отсюда можно получить, что
μ·R
= Rμ
=
![]()
Rμ = Rун .
Таким образом, для одного киломоля идеального газа уравнение состояния будет одинаковым для всех газов:
p·Vμ = Rμ·T (1.13)
Это уравнение носит название уравнение Клапейрона – Менделеева.
С помощью формулы
R
=
![]() (1.14)
(1.14)
можно определить газовую постоянную R для любого газа.
Масса одного киломоля сухого воздуха находится по уравнению:
μвозд
=
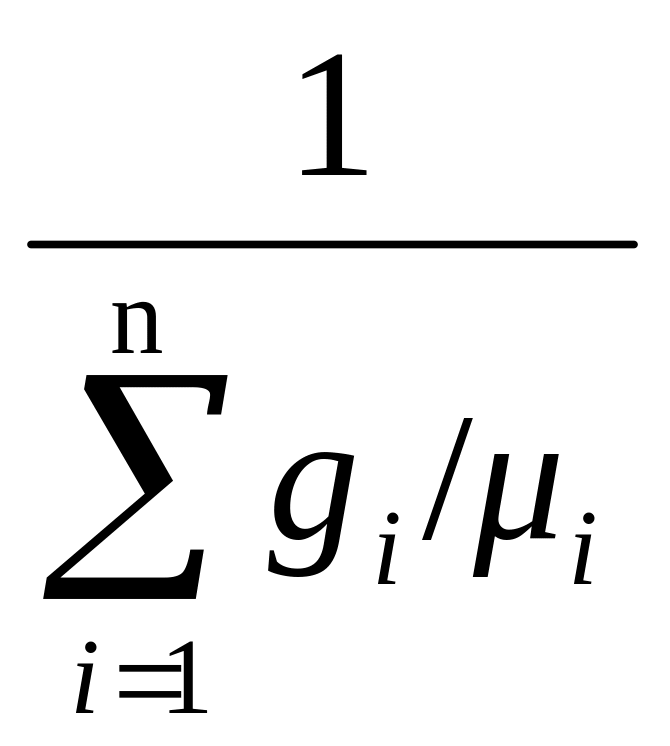 , (1.15)
, (1.15)
где gi = mi /mсм – массовая доля газа или отношение массы газа к общей массе смеси;
μi – молекулярная масса одного киломоля i-го газа в составе смеси, кг/кмоль.
Пользуясь таблицей 1.1., получаем
μвозд = 1/(0,78084/28,0134 + 0,209476/31,9968 + 0,934/39,3440 +
+ 0,0314/44,0079 + и т.д.) = 28,966 кг/кмоль.
Таким образом, газовая постоянная сухого воздуха равна
Rвозд
=
![]() = 287 Дж/(кг·К).
= 287 Дж/(кг·К).
Рассуждая аналогичным образом можно вычислить газовую постоянную для продуктов сгорания для газотурбинных двигателей (ГТД), она получается равной
Rг = 288 Дж/(кг·К).
