
- •Термодинамика и теплопередача. Учебное пособие
- •Раздел I. Техническая термодинамика
- •Содержание
- •Раздел I
- •Тема 1. Газ, как рабочее тело термодинамических систем
- •Тема 2. Первый закон термодинамики
- •Тема 3. Термодинамические процессы
- •Тема 4. Второй закон термодинамики
- •Тема 5. Идеальные циклы тепловых двигателей
- •Основные условные обозначения
- •Основные сечения потока
- •Сокращения
- •Используемые индексы
- •Предисловие
- •Введение
- •Раздел I техническая термодинамика
- •Тема 1. Газ, как рабочее тело термодинамических систем
- •1.1. Структура основных понятий термодинамики авиационных гтд
- •1.2. Основные понятия и определения термодинамики
- •1.3. Реальный и идеальный газы. Параметры состояния рабочего тела
- •1.3.1. Давление
- •1.3.2. Температура
- •1.3.3. Удельный объём, плотность
- •1.4. Уравнение состояния идеального и реального газов
- •1.4.1. Уравнение состояния идеального газа
- •1.4.2. Уравнение состояния реального газа
- •1.5. Понятие о термодинамическом процессе. Равновесные (обратимые) и неравновесные (необратимые) процессы
- •1.5.1. Равновесные (обратимые) процессы
- •1.5.2. Графическое изображение термодинамического процесса
- •1.5.3. Неравновесные (необратимые) процессы
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 2. Первый закон термодинамики
- •2.1. Внутренняя энергия рабочего тела. Изменение внутренней энергии
- •2.2. Работа газа, как форма передачи энергии в термодинамическом процессе
- •2.3. Теплота, как форма передачи энергии в термодинамическом процессе
- •2.4. Энтропия. Энтропийная “t-s” диаграмма
- •2.5. Зависимость количества работы и теплоты от характера термодинамического процесса
- •2.6. Теплоёмкость газа. Уравнение Майера. Показатель адиабаты
- •2.7. Энтальпия
- •2.8. Техническая работа (работа движущегося газа)
- •2.9. Содержание и уравнение первого закона термодинамики
- •2.10. Чистые вещества и смеси газов
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 3. Термодинамические процессы
- •3.1. Последовательность и объём расчёта термодинамических процессов
- •3.2. Изохорный процесс: определение, осуществление и исследование
- •3.2.1. Исследование изохорного процесса
- •3.3. Изобарный процесс: определение, осуществление и исследование
- •3.3.1. Исследование изобарного процесса
- •3.4. Изотермический процесс: определение, осуществление, исследование
- •3.4.1. Исследование изотермического процесса
- •3.5. Адиабатный (изоэнтропический) процесс: определение, осуществление, исследование
- •3.5.1. Исследование адиабатного процесса
- •3.6. Сравнение адиабаты и изотермы
- •3.7. Обобщающее значение политропных процессов
- •3.8. Энтальпийная “I-s” диаграмма (“I-s” координаты)
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 4. Второй закон термодинамики
- •4.1. Понятие о круговых процессах (циклах). Прямой цикл (цикл тепловой машины)
- •4.2. Полезная работа цикла. Термический кпд цикла
- •4.3. Цикл Карно и теорема Карно
- •4.4. Обратные циклы (циклы холодильных машин)
- •4.5. Второй закон термодинамики. Формулировки второго закона термодинамики
- •4.6. Второй закон термодинамики и энтропия
- •4.7. Статистическая интерпретация второго закона термодинамики
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Информация к размышлению
- •Проверьте, как Вы усвоили материал
- •Тема 5. Идеальные циклы тепловых двигателей
- •5.1. Особенности термодинамического метода исследования циклов тепловых двигателей
- •5.2. Схема устройства и принцип работы авиационного газотурбинного двигателя (гтд)
- •5.3. Идеальный цикл гтд (цикл Брайтона – Стечкина)
- •5.4. Работа и термический кпд цикла гтд
- •5.6. Сравнение циклов Брайтона и Гемфри
- •5.7. Цикл с регенерацией тепла
- •5.8. Цикл со ступенчатым подводом тепла
- •5.9. Эксергетический метод термодинамического анализа
- •5.10. Идеальные циклы двигателей внутреннего сгорания (двс)
- •5.10.1. Идеальный цикл двс с подводом тепла
- •5.10.2. Идеальный цикл двс с подводом тепла при постоянном
- •5.10.3. Сравнение циклов Отто и Дизеля
- •5.10.4. Цикл двс со смешанным теплоподводом
- •Примеры решения задач
- •Решение
- •Решение
- •4. Эффективность цикла оцениваем по величине термического кпд цикла
- •Решение
- •Проверьте, как Вы усвоили материал
- •Заключение
- •Список использованной литературы
- •Приложение
- •Международная стандартная атмосфера (мса) гост 4401–81 (фрагмент)
- •Теплофизические величины
- •Соблюдайте гост 8.417 – 2002
3.6. Сравнение адиабаты и изотермы
Сравнивая графики изотермического и адиабатного процессов можно заметить их внешнее сходство, поэтому важно уметь различать каким образом эти две зависимости (графики) располагаются относительно друг друга при одинаковых начальных параметрах рабочего тела.
Рассмотрим процесс
расширения рабочего тела (рис. 3.9,а) из
состояния 1 с параметрами p1,
υ1
по изотерме 1–2 в состояние 2 с параметрами
p2,
υ2,
и по адиабате 1–2' в состояние 2' с
параметрами
![]() ,
υ2.
Согласно уравнению изотермического
расширения p
= R·T/υ
= const/υ,
с увеличением удельного объёма υ
рабочего тела происходит пропорциональное
уменьшение его рабочего давления p.
А при адиабатном расширении (p
= R·T/υ)
удельный объём υ
увеличивается
на ту же величину, что и в изотермическом
процессе, но кроме этого происходит
уменьшение температуры, т.к. в адиабатном
процессе работа расширения осуществляется
за счёт уменьшения внутренней энергии
рабочего тела. Поэтому уменьшение
давления в адиабатном процессе происходит
более интенсивно, чем в изотермическом
процессе. Следовательно, адиабата будет
протекать более круче, чем изотерма, и
в процессе расширения она располагается
ниже изотермы (рис. 3.9,а). А в процессе
сжатия адиабата располагается выше
изотермы (рис. 3.9,б).
,
υ2.
Согласно уравнению изотермического
расширения p
= R·T/υ
= const/υ,
с увеличением удельного объёма υ
рабочего тела происходит пропорциональное
уменьшение его рабочего давления p.
А при адиабатном расширении (p
= R·T/υ)
удельный объём υ
увеличивается
на ту же величину, что и в изотермическом
процессе, но кроме этого происходит
уменьшение температуры, т.к. в адиабатном
процессе работа расширения осуществляется
за счёт уменьшения внутренней энергии
рабочего тела. Поэтому уменьшение
давления в адиабатном процессе происходит
более интенсивно, чем в изотермическом
процессе. Следовательно, адиабата будет
протекать более круче, чем изотерма, и
в процессе расширения она располагается
ниже изотермы (рис. 3.9,а). А в процессе
сжатия адиабата располагается выше
изотермы (рис. 3.9,б).

Рис. 3.9. Сравнение адиабаты и изотермы: а – процесс расширения газа,
б – процесс сжатия газа
3.7. Обобщающее значение политропных процессов
Реальные процессы в элементах авиационных двигателей протекают при наличии теплообмена и с изменением параметров рабочего тела (p, υ, T). Естественно реальные процессы не могут быть описаны ранее полученными закономерностями для основных термодинамических процессов. Поэтому используют другие процессы, более близкие к действительным термодинамическим процессам, протекающим в авиационных двигателях. Наиболее простым из них считают политропный процесс – это термодинамический процесс, при осуществлении которого может изменяться любой из параметров состояния (p, υ, T), а также возможен теплообмен с окружающей средой.
Примерами политропных процессов могут служить процессы сжатия и расширения рабочего тела в ГТД с учётом сил трения.
1. Уравнение процесса: p·υn = const, где n показатель политропы. Показатель n может быть любым числом (–∞ < n < +∞), следовательно, политропных процессов бесконечное множество. Но в каждом конкретном процессе величина n постоянна.
2. Поскольку уравнение политропного процесса совпадает по форме с адиабатным, то легко можно получить соотношения между параметрами в начале и в конце политропного процесса, заменив в формулах (3.34), (3.37), (3.39) показатель адиабаты k на показатель политропы n.
 ;
;
 (3.47)
(3.47)
 ;
;
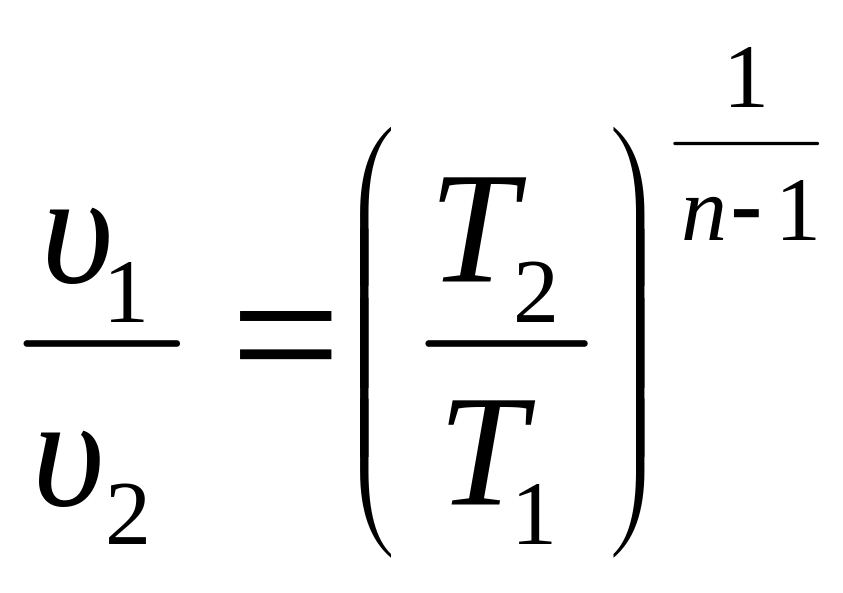 (3.48)
(3.48)
 ;
;
 (3.49)
(3.49)
При исследовании реальных процессов необходимо бывает установить, является ли данный процесс политропным, а затем определяется показатель политропы n из уравнения (3.47) по значению параметров газа в каких–либо двух точках этого процесса.
lg![]() ,
т.е. n
=
,
т.е. n
=
![]() .
(3.50)
.
(3.50)
Для каждого из реальных необратимых процессов значения показателей политропы лежат в тех диапазонах, которые определяются расположением кривой реального процесса. Так в реальном компрессоре кривая процесса сжатия располагается между адиабатной (n = k) и изохорой (n = ± ∞) линия О…комп. (рис. 3.10.). Следовательно теоретически показатель политропы процесса сжатия в компрессоре nкомп. (k < n комп. < ∞) ненамного превышает показатель адиабаты k.
Обработка показателей многих компрессоров показывает, что nкомп. = 1,46…1,47 > kвозд. = 1,41.
В реальной газовой турбине кривая процесса расширения линия О…турб. (рис. 3.10.) лежит между адиабатой (n = k) и изохорой (n = 1) и теоретически k < nтурб. < 1. Но практически, показатель политропы процесса расширения в турбине nтурб. гораздо ближе к показателю адиабаты и составляет
nтурб. = 1,27…1,29 < kг для продуктов сгорания kг = 1,33.
3. Определение величин, входящих в первый закон термодинамики
а) qn = Сn·(T2 – T1), (3.51)
где Сn – теплоёмкость газа в политропном процессе.
б) –∆U = Cυ·(T2 – T1) (3.52)
в) Ln
=
![]() .
(3.53)
.
(3.53)
Это уравнение по форме одинаково с соответствующим уравнением для адиабатного процесса и отличается от него только значением показателя политропы n.
Найдём формулу для вычисления Сn в произвольном политропном процессе. Для этого подставим в уравнение первого закона термодинамики величины qn, ∆U, Ln их аналитическое выражение. В результате получим:
qn = ∆U + Ln
Сn·∆T
= Cυ·∆T
+
![]()
Сn
= Cυ
+
![]() или Сn
= Cυ
·
или Сn
= Cυ
·![]() .
(3.54)
.
(3.54)
Из этого выражения видно, что если считать теплоёмкость Cυ не зависящей от температуры, то Сn для идеального газа в политропном процессе будет постоянна и её можно всегда найти, зная Cυ, R и n.
4. Каждому политропному процессу соответствует своё распределение энергии. Поскольку таких процессов множество, исследовать их все не представляется возможным. Однако качественное суждение о характере распределения энергии в любом политропном процессе можно сделать, рассмотрев его расположение по отношению к известным нам процессам: изохорному, изобарному, изотермическому и адиабатному (рис. 3.10.), которые являются частными случаями политропных процессов. Уравнение каждого из них можно представить в виде p·υn = const со своим значением показателя политропы.
Действительно, при n = 0 уравнение политропы получает вид:
p·υ° = p·1 = const или p = const (изобарный процесс).
Изобарный процесс (n = 0) делит область политропных процессов на две части. Процессы, графики которых расположены выше изобары, происходят с увеличением давления, ниже изобары – с уменьшением давления.
При n = 1 уравнение политропы описывает изотермический процесс:
p·υ1 = p·υ = const.
Изотермический процесс разделяет все процессы на две группы. Политропы, расположенные выше изотермы соответствуют процессам, которые сопровождаются увеличением внутренней энергии (повышением температуры), ниже изотермы – уменьшением внутренней энергии (понижением температуры).
При n = k, политропы совпадают с адиабатой:
p·υk = const.
Адиабатный процесс (n = k) делит все политропные процессы на две группы. Если политропа расположена выше адиабаты, ей соответствует процесс, который протекает с подводом теплоты (q > 0) к рабочему телу, а если ниже адиабаты, то с отводом теплоты (q < 0) от рабочего тела.
При n = ± ∞ (при очень больших абсолютных значениях n) уравнение политропы преобразуется в уравнение изохоры, извлекая корень степени n из уравнения политропы, получим:
![]() .
.
При n
→ ± ∞ величина
![]() ,
,![]() ,
следовательно, при n
= ± ∞ получаем υ
= const.
,
следовательно, при n
= ± ∞ получаем υ
= const.
Изохорный процесс (n = ± ∞) разделяет всю область политропных процессов на две части. Политропы, расположенные справа от изохоры, соответствуют процессам, которые осуществляются с увеличением объёма, следовательно, газом совершается при этом работа расширения против внешних сил (L > 0). Если политропы расположены слева от изохоры, то такой процесс происходит с уменьшением объёма. При этом внешние силы совершают над газом работу (L < 0), сжимая его.
Таким образом, если известны показатель политропы и характер или график процесса, то можно определить при каких условиях он может осуществляться: с подводом или отводом теплоты, с увеличением или уменьшением внутренней энергии, совершением механической работы рабочим телом или внешними силами над рабочим телом.
Покажем области политропных процессов в зависимости от показателя политропы в координатах “p-υ” и “T-s”.

Рис. 3.10. Области политропных процессов: а – в “p-υ” координатах,
б – в “T-s” координатах
