
- •Термодинамика и теплопередача. Учебное пособие
- •Раздел I. Техническая термодинамика
- •Содержание
- •Раздел I
- •Тема 1. Газ, как рабочее тело термодинамических систем
- •Тема 2. Первый закон термодинамики
- •Тема 3. Термодинамические процессы
- •Тема 4. Второй закон термодинамики
- •Тема 5. Идеальные циклы тепловых двигателей
- •Основные условные обозначения
- •Основные сечения потока
- •Сокращения
- •Используемые индексы
- •Предисловие
- •Введение
- •Раздел I техническая термодинамика
- •Тема 1. Газ, как рабочее тело термодинамических систем
- •1.1. Структура основных понятий термодинамики авиационных гтд
- •1.2. Основные понятия и определения термодинамики
- •1.3. Реальный и идеальный газы. Параметры состояния рабочего тела
- •1.3.1. Давление
- •1.3.2. Температура
- •1.3.3. Удельный объём, плотность
- •1.4. Уравнение состояния идеального и реального газов
- •1.4.1. Уравнение состояния идеального газа
- •1.4.2. Уравнение состояния реального газа
- •1.5. Понятие о термодинамическом процессе. Равновесные (обратимые) и неравновесные (необратимые) процессы
- •1.5.1. Равновесные (обратимые) процессы
- •1.5.2. Графическое изображение термодинамического процесса
- •1.5.3. Неравновесные (необратимые) процессы
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 2. Первый закон термодинамики
- •2.1. Внутренняя энергия рабочего тела. Изменение внутренней энергии
- •2.2. Работа газа, как форма передачи энергии в термодинамическом процессе
- •2.3. Теплота, как форма передачи энергии в термодинамическом процессе
- •2.4. Энтропия. Энтропийная “t-s” диаграмма
- •2.5. Зависимость количества работы и теплоты от характера термодинамического процесса
- •2.6. Теплоёмкость газа. Уравнение Майера. Показатель адиабаты
- •2.7. Энтальпия
- •2.8. Техническая работа (работа движущегося газа)
- •2.9. Содержание и уравнение первого закона термодинамики
- •2.10. Чистые вещества и смеси газов
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 3. Термодинамические процессы
- •3.1. Последовательность и объём расчёта термодинамических процессов
- •3.2. Изохорный процесс: определение, осуществление и исследование
- •3.2.1. Исследование изохорного процесса
- •3.3. Изобарный процесс: определение, осуществление и исследование
- •3.3.1. Исследование изобарного процесса
- •3.4. Изотермический процесс: определение, осуществление, исследование
- •3.4.1. Исследование изотермического процесса
- •3.5. Адиабатный (изоэнтропический) процесс: определение, осуществление, исследование
- •3.5.1. Исследование адиабатного процесса
- •3.6. Сравнение адиабаты и изотермы
- •3.7. Обобщающее значение политропных процессов
- •3.8. Энтальпийная “I-s” диаграмма (“I-s” координаты)
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 4. Второй закон термодинамики
- •4.1. Понятие о круговых процессах (циклах). Прямой цикл (цикл тепловой машины)
- •4.2. Полезная работа цикла. Термический кпд цикла
- •4.3. Цикл Карно и теорема Карно
- •4.4. Обратные циклы (циклы холодильных машин)
- •4.5. Второй закон термодинамики. Формулировки второго закона термодинамики
- •4.6. Второй закон термодинамики и энтропия
- •4.7. Статистическая интерпретация второго закона термодинамики
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Информация к размышлению
- •Проверьте, как Вы усвоили материал
- •Тема 5. Идеальные циклы тепловых двигателей
- •5.1. Особенности термодинамического метода исследования циклов тепловых двигателей
- •5.2. Схема устройства и принцип работы авиационного газотурбинного двигателя (гтд)
- •5.3. Идеальный цикл гтд (цикл Брайтона – Стечкина)
- •5.4. Работа и термический кпд цикла гтд
- •5.6. Сравнение циклов Брайтона и Гемфри
- •5.7. Цикл с регенерацией тепла
- •5.8. Цикл со ступенчатым подводом тепла
- •5.9. Эксергетический метод термодинамического анализа
- •5.10. Идеальные циклы двигателей внутреннего сгорания (двс)
- •5.10.1. Идеальный цикл двс с подводом тепла
- •5.10.2. Идеальный цикл двс с подводом тепла при постоянном
- •5.10.3. Сравнение циклов Отто и Дизеля
- •5.10.4. Цикл двс со смешанным теплоподводом
- •Примеры решения задач
- •Решение
- •Решение
- •4. Эффективность цикла оцениваем по величине термического кпд цикла
- •Решение
- •Проверьте, как Вы усвоили материал
- •Заключение
- •Список использованной литературы
- •Приложение
- •Международная стандартная атмосфера (мса) гост 4401–81 (фрагмент)
- •Теплофизические величины
- •Соблюдайте гост 8.417 – 2002
3.3. Изобарный процесс: определение, осуществление и исследование
Термодинамический процесс, протекающий при постоянном давлении рабочего тела, называется изобарным (от греческих слов изос – равный и барос – тяжесть).
Примером процесса, близкого к изобарному, является процесс подвода теплоты к рабочему телу в камерах сгорания авиационных ГТД.
3.3.1. Исследование изобарного процесса
1. Условие протекания процесса и есть уравнения процесса
p = const. (3.12)
Используя уравнение состояния идеального газа, получим уравнение изобарного процесса через параметры состояния
υ
=
![]() =
(const)·T
или
υ
= f(T)
. (3.13)
=
(const)·T
или
υ
= f(T)
. (3.13)
2. Из уравнения 3.13 очевидно, что удельный объём в изобарном процессе изменяется пропорционально абсолютной температуре
![]() .
(3.14)
.
(3.14)
Если подводить теплоту к рабочему телу, его удельный объём (υ) и температура (Т) возрастают, а давление (р) останется неизменным (р = const). Физически это объясняется тем, что уменьшение числа молекул, приходящихся на единицу площади поверхности, вызванное ростом удельного объёма, компенсируется увеличением силы ударов каждой молекулы, обусловленным увеличением температуры (энергии) молекул.
3. Графическое построение процесса.
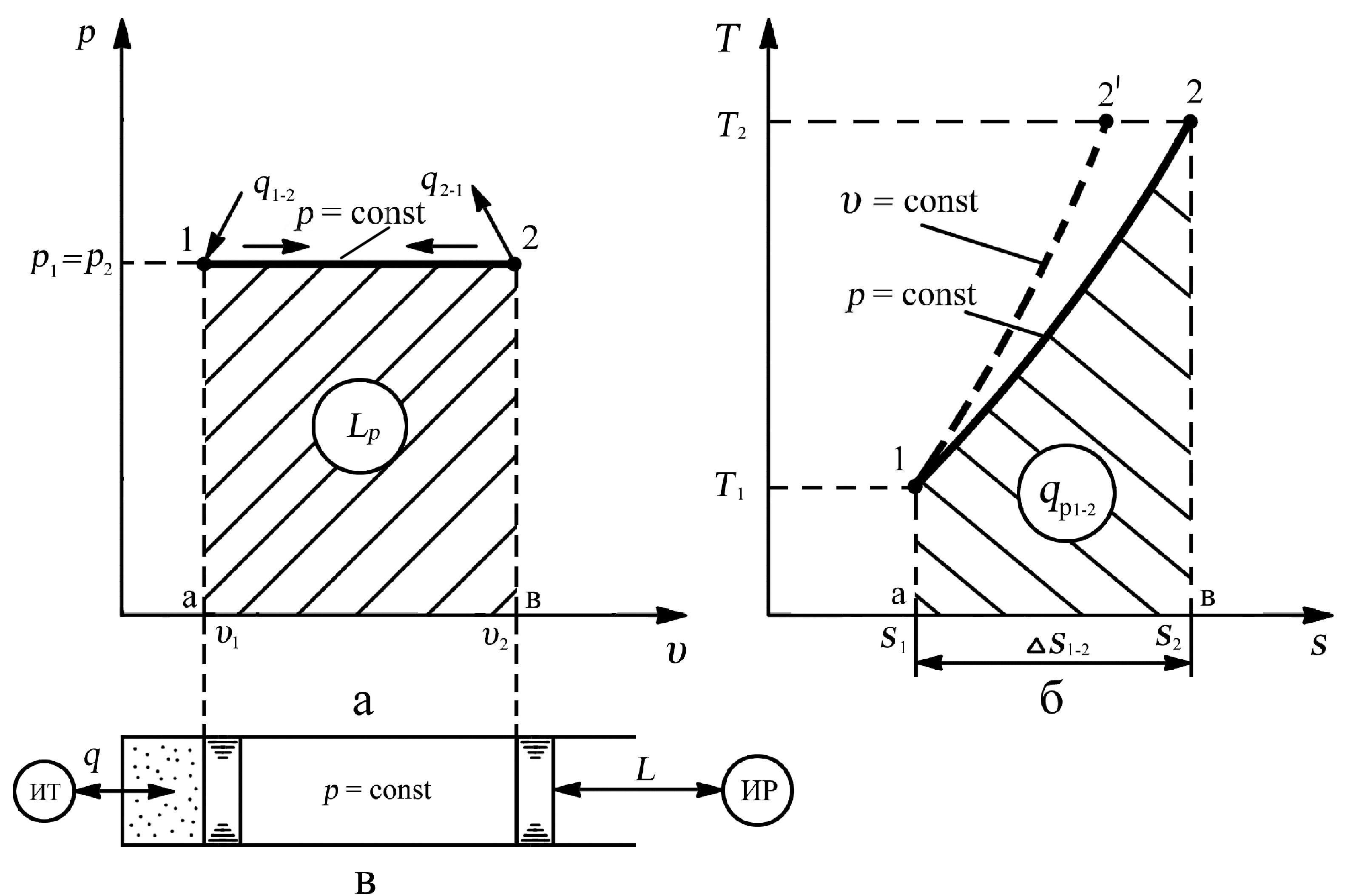
Рис. 3.3. Изобарный процесс: а – рабочая диаграмма процесса, б – тепловая диаграмма процесса, в – осуществление процесса
4. Определение величин входящих в первый закон термодинамики
а) qp = = Cp·(T2 – T1); (3.15)
б) ∆Up
=
 = Cυ·(T2
– T1);
(3.16)
= Cυ·(T2
– T1);
(3.16)
в) Lp = = p·(υ2 – υ1) = R·(T2 – T1). (3.17)
Из формулы (3.17) видно, что работа расширения–сжатия совпадает с работой проталкивания. Следовательно, в открытой ТДС работа L расходуется на перемещение газа из области высокого в область низкого давления в процессе расширения. Такой процесс происходит в камере сгорания ГТД.
Таким образом, теплота, подводимая к рабочему телу в изобарном процессе, расходуется на увеличение внутренней энергии рабочего тела и совершения работы против внешних сил.
qp = ∆Up + Lp (3.18)
Теплота qp 1-2 , участвующая в изобарном процессе определяется из тепловой диаграммы (рис. 3.2,б). Площадь под линией процесса в тепловой “T-s” диаграмме даёт qp 1-2
qp
1-2
= пл. а12в ≈
![]() =
.
(3.19)
=
.
(3.19)
г) Определим изменение энтропии для изобарного процесса, используя аналитическое выражение первого закона термодинамики через энтальпию (2.44).
qp 1-2 = T·ds = di + υ·dp,
т.к. для изобарного процесса p = const и учитывая, что dp = 0, получаем:
qp 1-2 = T·ds = di = Сp·dT . (3.20)
Из уравнения (3.20) следует, что вся теплота, подведённая к рабочему телу, идёт на изменение энтальпии.
Проинтегрируем
выражение (3.20) =>
 и определим изменение энтропии ∆s1-2
при конечном изменении температуры Т,
при интегрировании считаем, что Сp
не зависит от Т
и окончательно получаем:
и определим изменение энтропии ∆s1-2
при конечном изменении температуры Т,
при интегрировании считаем, что Сp
не зависит от Т
и окончательно получаем:
∆s1-2
= s2
– s1
= Cp·ln
= Cp·ln![]() = Cp·2,3·lg
= Cp·2,3·lg![]() .
(3.21)
.
(3.21)
5. Распределение энергии, количественно оценивает коэффициент
α =![]() .
(3.22)
.
(3.22)
Для воздуха k
= 1,41, поэтому из (3.22) имеем, что ∆U
=
![]() .
Это означает, согласно первому закону
термодинамики, что
из подведённого тепла q
в изобарном процессе бόльшая часть (
.
Это означает, согласно первому закону
термодинамики, что
из подведённого тепла q
в изобарном процессе бόльшая часть (![]() )
расходуется на изменение внутренней
энергии рабочего тела, а меньшая часть
(
)
расходуется на изменение внутренней
энергии рабочего тела, а меньшая часть
(![]() )
идёт на совершение работы против внешних
сил (рис.
3.4,а и 3.4,б).
)
идёт на совершение работы против внешних
сил (рис.
3.4,а и 3.4,б).

Рис. 3.4. Распределение энергии в изобарном процессе: а – при подводе теплоты к рабочему телу (процесс 1–2), б – при отводе теплоты от рабочего тела (процесс 2–1)
Из сравнения графиков изохорного и изобарного процессов в тепловой “T-s” диаграмме (рис. 3.3,б) можно заметить их внешнее сходство, поэтому важно уметь различать, каким образом эти две зависимости υ = const (линия 1–2') и p = const (линия 1–2) располагаются относительно друг друга при одинаковых начальных параметрах рабочего тела. Изохора в тепловой “T-s” диаграмме будет круче, чем изобара в тех же координатах по той причине, что подведённое тепло в изохорном процессе идёт только на увеличение внутренней энергии рабочего тела, естественно повышение температуры рабочего тела происходит более интенсивно, чем в изобарном процессе, в котором часть подведённого тепла идёт ещё на совершение работы.
