Игры с частными случаями платежных матриц

При анализе игры используются следующие свойства платежных матриц:

1. Произведение матрицы на число.

, , , .

Стратегии игроков не меняются, увеличивается только цена игры

.

При получается проигрыш.

2. Прибавляем к элементам матрицы положительное число

,

,

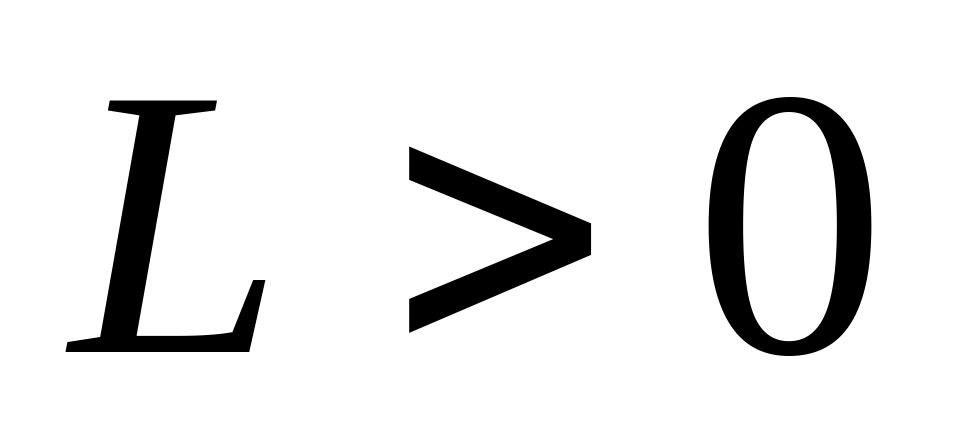
, оптимальные стратегии не меняются.

Латинский квадрат.

Латинским квадратом называют матрицу , если каждая из ее строк (столбцов) состоит из чисел от 1 до m.

Пример:

.

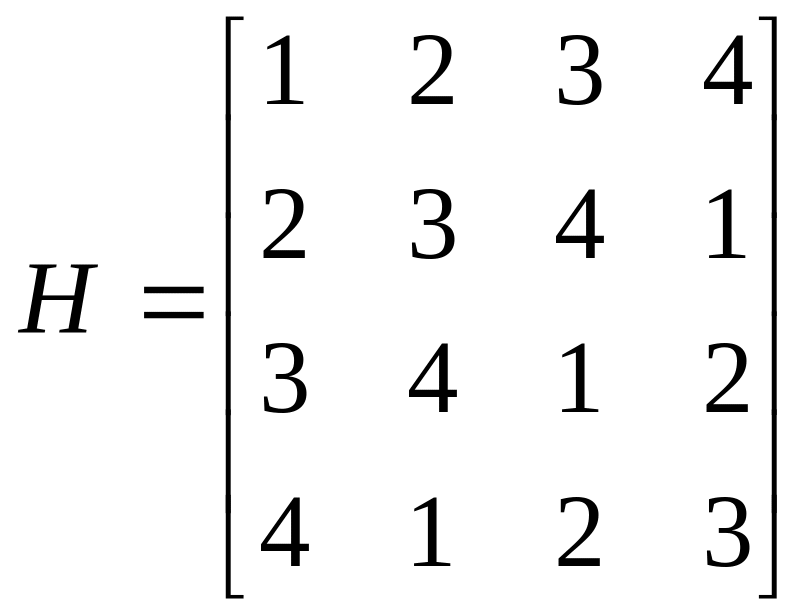Для таких матриц справедливо следующее соотношение, определяющее цену игры: . В данном примере цена игры равна 2,5.

Диагональная игра.

, , где — символ Кронекера.

При такой матрице диагональные элементы можно преобразовать в . В оптимальные стратегиях игроков входят все чистые стратегии .

, , — диагональные элементы.

Аналогично для второго игрока:

.

Пример:

2 кг ершей, 3 кг щуки. С какой вероятностью надо выбирать поход за ершами?

.

Делаем вывод, что за ершами надо ходить чаще.

Если все , то , .

Игра, у которой диагональные элементы равны -1, а остальные равны 1.

Пусть матрица выигрышей имеет произвольный порядок m:

, , .

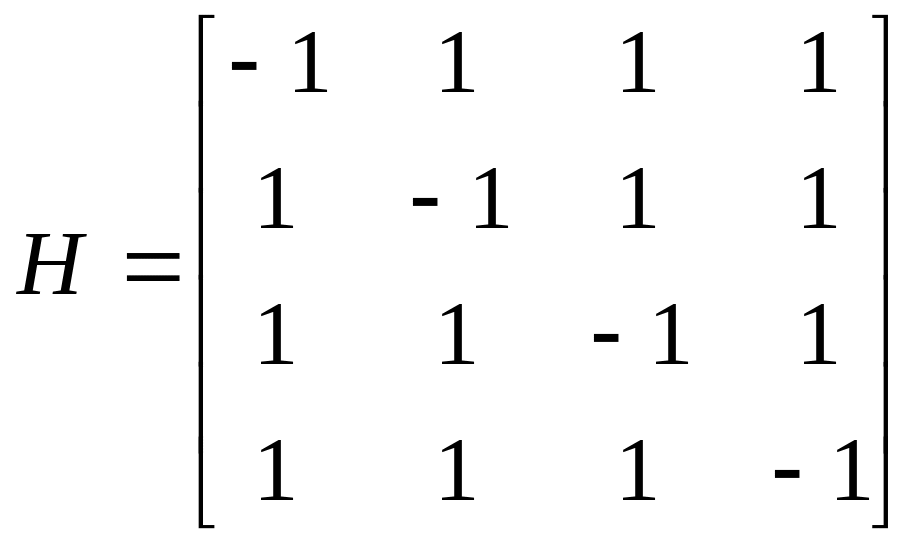Для диагональных игр все стратегии являются рабочими (полезными), в других играх число полезных стратегий .

Теорема о поведении игроков. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш игроков неизменен и равен цене игры, если второй игрок не выходит за пределы своих полезных (рабочих) стратегий. Размер выигрыша не зависит от того, какую из чистых или смешанных стратегий он использует.

Решение матричных игр

Существует несколько основных методов решения матричных игр:

1. Аналитический

2. Графический

3. Итеративный (метод Брауна-Джонсона)

4. Метод линейного программирования

Рассмотрим подробнее последний из перечисленных.

Линейное программирование для решения матричных игр

Пусть имеется некоторая матричная игра Г=<X,Y,H> (где X и Y — множества стратегий 1го и 2го игроков соответственно, а Н — платежная матрица), H=(a_ij) R^m*n

Требуется найти оптимальную смешанную стратегию, т.е.

p^*=(p₁^*,p₂^*,…,p_m^*) и q*=(q₁^*,q₂^*,…,q_n^*), при которых

,

где v — цена игры.

Для решения этой задачи можно применять линейное программирование.

Будем считать, что все a_ij 0, игра Г’ эквивалентна игре Г, H’=H+L, L — число, при котором неравенство будет выполняться (при переходе от игры Г к игре Г’).

Далее предположим, что 2й игрок принимает стратегию y_k , , тогда выигрыш игрока 1 будет определяться условием

p₁a_1k + p₂a_2k + … + p_ma_mk v, (*)

(равенство v достигается, если k-я стратегия является рабочей)

p_i 0 , ; p_i a_ik > 0 v>0 (т.к. левая часть неравенства (*) больше нуля).

Разделим неравенство (*) на v :

t₁a_1k + t₂a_2k +…+ t_ma_mk 1, где t_i= , t_i 0,

Цель стратегии 1-го игрока — максимизировать выигрыш:

v max min

Исходя из рассмотренных условий, задачу линейного программирования можно сформулировать так:

1) t_i 0 ,

2) min

3) , причем z_k=0 для рабочих стратегий , z_k>0 для нерабочих стратегий.

Решение этой задачи позволяет:

1. Вычислить t_i^*.

2. Определить те k, при которых z_k=0 (т.е. найти рабочие стратегии 2го игрока)

3. 

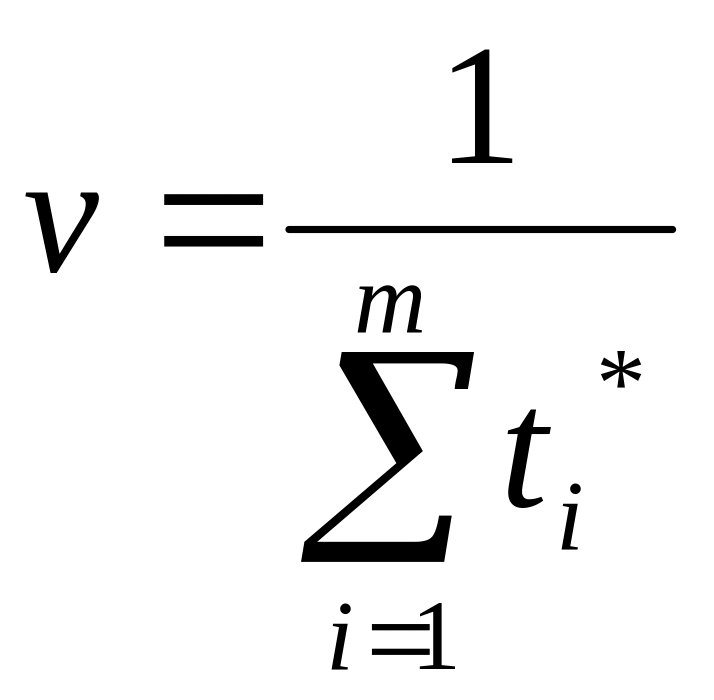
4. p_i^*=t_i^* v

Для определения стратегии 2го игрока можно поступить двояко:

1. сформулировать двойственную задачу

2. использовать информацию о полезных стратегиях 2-го игрока (полезные стратегии – при z_k=0 )

Пусть найдена полезная стратегия игрока y_j, , . Для определения оптимальной стратегии q_j^*, для рабочих стратегий 1-го игрока можно записать условие

q₁a_i1 + q₂a_i2 + … + q_ka_ik v,

(причем если i-я стратегия 1-го игрока рабочая, то =v,а если нет, то >v)

q₁a_i1 + q₂a_i2 + … + q_ka_ik v ,

- система уравнений для определения оптимального q.

ПРИМЕР.

Пусть имеется некоторая игра с матрицей A=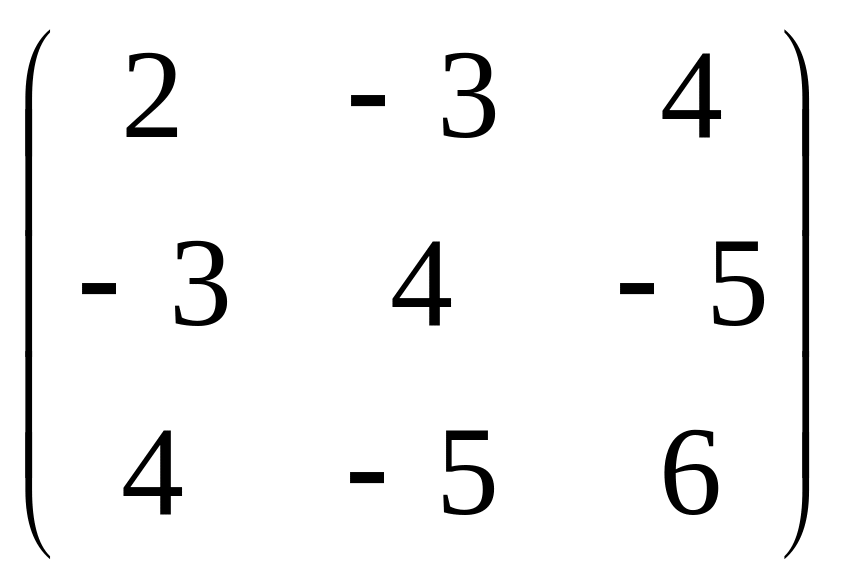

A+5 A₁=

Предположим, что все стратегии рабочие. Составляем систему уравнений:

7t₁ + 2t₂ + 9t₃ - z₁ = 1

2t₁ + 9t₂ - z₂ = 1

9t₁+11t₃ - z₃ = 1

Решение этих уравнений при условии t₁ + t₂ + t₃ min :

t₁ = 0,05

t₂ = 0,1

t₃ = 0,05

v(A₁) = = 5 p₁=0,05*5=0,25

p₂=0,1*5=0,5

p₃=0,05*5=0,25

v(A)=v(A₁) - 5=0 игра справедливая. Найдём стратегию второго игрока:

q₁^* + q₂^* + q₃^* = 1

2q₁ + 9q₂ = 5 q₁=q₃=0,25

9q₁ + 11q₃ =5 q₂=0,5