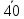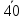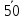МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Рязанский государственный радиотехнический университет»

Экзаменационная работа

на тему

«Критерий Вилкоксона, Манна, Уитни. Ранговая корреляция .Метод моментов. Метод максимального правдоподобия»

Выполнила:

Студентка гр. 942

Фёдорова М. В.

Проверила

Ст. пр. Орлова С. Н.

Рязань, 2012

1. Теоретическая часть

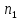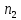1.1 Критерий Вилкоксона, Манна и Уитни. Критерий применяется для сравнения двух независимых выборок объема и и проверяет гипотезу Н₀, утверждающую, что выборки получены из однородных генеральных совокупностей и, в частности, имеют равные средние и медианы.

Статистика W критерия определяется следующим образом. Расположим 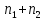значений объединенной выборки в порядке возрастания, т. е. в виде вариационного ряда. Каждому элементу ряда поставим в соответствие его номер в ряду — ранг. Если несколько элементов ряда совпадают по величине, то каждому из них присваивается ранг, равный среднему арифметическому их номеров. Последний элемент в ранжированной объединённой выборке должен иметь ранг 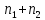. Этот факт можно использовать при проверке правильности ранжирования.

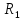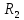Пусть — сумма рангов первой выборки, — сумма рангов второй выборки. Вычислим значения 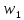и :

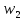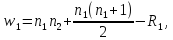
Правильность вычислений проверяется по формуле:

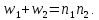
Выборочное значение 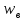статистики критерия есть наименьшее из чи­сел 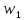и 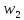. В таблице П 10 приводятся вероятности того, что W < 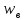, при условии, что гипотеза Н₀ верна, т. е. значения

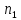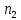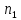для выборок объема и (≥). При односторонней (двусторон­ней) альтернативной гипотезе Н₁, гипотеза Н₀ отклоняется, если р≤α (р ≤α/2), где α — заданный уровень значимости. В противном случае гипотеза Н₀ не противоречит результатам наблюдений.

Если объем каждой из выборок больше 8, то проверку гипотезы Н₀ можно проводить, используя статистику

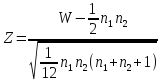
имеющую (при условии, что верна гипотеза Н₀) приблизительно нор­мальное распределение N(0, 1). В этом случае гипотеза Н₀ отклоняется на уровне значимости α, если выборочное значение 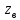статистики Z удовлетворяет неравенству

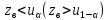
при левосторонней (правосторонней) альтернативной гипотезе Н₁ и если

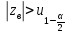
при двусторонней альтернативной гипотезе Н₁.

Пример. Измерялось напряжение пробоя у диодов, отоб­ранных случайным образом из двух партий. Результаты измерения (в вольтах) следующие:

1-я партия	39	50	61	67	40	40	54	-
2-я партия	60	53	42	41	40	54	63	69

Можно ли считать, что у диодов из второй партии напряжение пробоя выше, чем у диодов из первой партии? Принять α = 0,10. Воспользуемся критерием Вилкоксона. Составим вариационный ряд, отмечая принадлежность элемента к первой партии черточкой сверху. В результате получим следующую ранжированную последовательность:

Элемент				40	41	42		53		54	60		63		69
Ранг	1	3	3	3	5	6	7	8	9,5	9,5	11	12	13	14	15

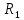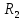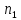Сумма рангов первой выборки = 49,5, сумма рангов второй выборки = 70,5, = 7, 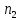= 8. По формулам находим

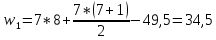
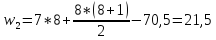
Используя соотношение, проверяем правильность вычислений:

34,5 + 21,5=56,

Выборочное значение статистики 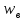равно меньшему нз чисел 34,5 и 21,5. т.е.

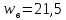
По таблице П 10 находим (с интерполяцией)

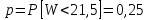
Так как предположение о том, что у диодов второй партии напряжение пробоя выше, соответствует односторонней альтернативной гипотезе Н_1х, а вероятность р = 0,25 превышает уровень значимости α = 0,1, гипо­теза Н₀ не противоречит результатам измерений. Следовательно, ре­зультаты измерений не дают оснований считать, что напряжение пробоя у диодов второй партии выше, чем у диодов первой партии.

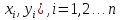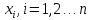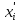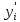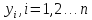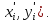2. Ранговая корреляция. Пусть ( — выборка наблюдений непрерывных случайных величин X и У. Каждому значению , поставим в соответствие ранг, т. е, номер элемента x_i в вариационном ряду. Аналогичным способом определим ранги элементов . Каждой паре ( таким образом, соответствует пара рангов ( Вычислим коэффициент корреляции по выборке рангов (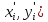, 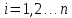. Полученное значение 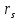называется выборочным значением рангового коэффициента корреляции Спирмена. Ранговый коэффициент корреляции, так же как и коэффициент корреляции 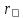, характеризует зависимость между случайными величинами X и У, но вычисляется значительно проще, а именно, справедлива следующая формула:

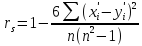
Поэтому при большом объеме выборки для оценки зависимости между случайными величинами используется ранговая корреляция. Коэффициент r_s является непараметрической мерой связи и, следова­тельно, может использоваться при произвольном непрерывном распре­делении генеральной совокупности, в то время как использование коэффициента Корреляции r предполагает двумерное нормальное рас­пределение генеральной совокупности. Гипотеза H_o: 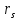, = 0 при аль­тернативной гипотезе H₁: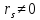, и при объеме выборки n>9 про­веряется по значению статистики

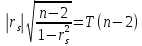
При условии, что верна гипотеза H_o, эта статистика имеет распределе­ние Стьюдента с n-2 степенями свободы. Если 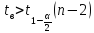, где α – заданный уровень значимости, то гипотеза H_o отклоняется, т. е. между X и У существует ранговая корреляционная зависимость.

Пример. Вычислить коэффициент ранговой корреляции для следующей выборки:

X	68,8	63,3	75,7	67,2	71,3	72,8	76,5	63,5	69,9	71,4
Y	167,0	113,3	159,9	153,6	150,8	181,2	173,1	115,4	125,6	166,2

Проверить значимость ранговой корреляции при α =0,10. Определим ранги элементов исходной выборки. Предварительно перепишем исходную выборку, упорядочив ее элементы по верхней строке (т. е. по значениям X), в результате получим

X	63,3	63,5	67,2	68,8	69,9	71,3	71,4	72,8	75,7	76,5
Y	113,3	115,4	153,6	167,0	125,6	150,8	166,2	181,2	159,9	173,1

Таким образом, упорядоченной по элементам х_i выборке соответствует следующая последовательность пар рангов и их разностей:

x’	1	2	3	4	5	6	7	8	9	10
y’	1	2	5	8	3	4	7	10	6	9
x’-y’	0	0	-2	-4	2	2	0	-2	3	1

Так как 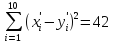, по формуле находим

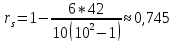
Проверим значимость полученного результата. Найдем выборочное значение статистики

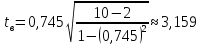
Так как .
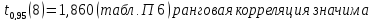