2. Метод моментов

Метод моментов был предложен статистиком К.Пирсоном. Его достоинство в сравнительной простоте, а суть в следующем: приравнивают теоретические моменты к эмпирическим моментам того же порядка. При этом получается уравнение относительно неизвестного параметра. Например,

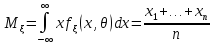
т.е. мы приравняли теоретический начальный момент 1-го порядка к эмпирическому начальному моменту 1-го же порядка. Если из уравнения можно найти θ, которое выражается как функция от переменных 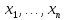, то ее прелставляют как точечную оценку математического ожидания. Аналогично, по уравнению

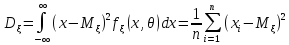
мы получим оценку для дисперсии. (Здесь мы приравняли 2-й центральный теоретический момент ко 2-му же эмпирическому моменту).

Пример. Пусть имеем 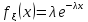– плотность показательного распределения с параметром λ. Согласно вышеизложенному методу имеем

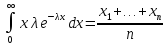
Вычисляя интеграл, получаем

- точечная оценка параметра λ.

2. Метод максимального правдоподобия

Метод предложен статистиком Р. Фишером. В качестве примеров рассмотрим разные варианты точечного оценивания математического ожидания. Пусть имеется ряд независимых измерений , :

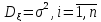а) пусть 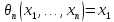(«оценка по первому впечатлению»). Несмещенность: 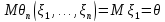дана в условии. Так как по существу не зависит от n и при n → ∞ не стремится к 0, то оценка 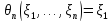, , 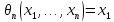не является состоятельной;

б) пусть 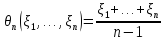. Тогда 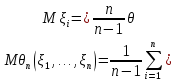– смещенная оценка. Однако она является состоятельной. Для доказательства используем неравенство Чебышева:

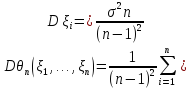
Отсюда по неравенству Чебышева:

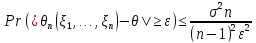
что при n → ∞ стремиться к 0;

в) пусть, наконец, 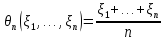– еще одна оценка параметра 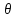. Легко видеть, что

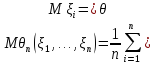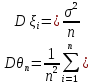и и

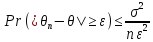стремится к 0 при n → ∞. Следовательно, оценка несмещенная состоятельная.

Таким образом, в приведенных примерах оценки (а), (б), (в) рассмотрены в порядке их «улучшения». Свойство эффективности оценок мы пока не берем во внимания.

Распространенным методом получения точечных оценок является метод максимального правдоподобия, «почти всегда» дающий смещенные, но состоятельные точечные оценки. Суть метода: пусть – плотность распределения изучаемой случайной величины и θ - его известный параметр распределения; пусть имеется вариационный рад. Строится функционал (функция правдоподобия)

….

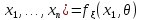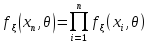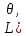
Находят максимум функции 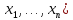по параметру θ и полученное значение 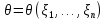определяет точечную оценку .

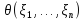Пример. По вариационному ряду независимых испытаний Бернулли 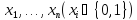дадим оценку параметра p(A) биномиального закона распределения.

Составим функцию правдоподобия

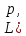
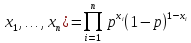(множитель 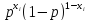дает p, если в i-ом испытании происходит событие A и 1-p, если происходит событие );

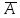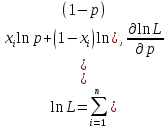
Итак, мы получили для p(A) несмещенную и состоятельную оценку

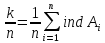
2. Практическая часть

Исходные данные:

x	2,98	2,23	2,35	2,28	2,29	2,32	2,36	2,39	2,12	2,44	2,50	2,97	2,86	2,17	2,11
y	1,03	1,78	1,37	1,15	1,48	1,77	1,46	1,49	1,97	1,25	1,27	1,10	1,05	1,86	1,97