1. Теория функций комплексной переменной (тфкп): История вопроса. Основные определения, понятие комплексной функции комплексной и действительной переменной. Кривые на комплексной плоскости. Примеры.

Опр.1. Комплексным числом c называется упорядоченная пара действительных чисел a и b: c = (a ,b).

Число a этой пары называется действительной частью комплексного числа c и обозначается символом Rec : a = Rec (от латинского слова realis – действительный), число b этой пары называется мнимой частью комплексного числа c и обозначается Im c: b = Im c (от латинского слова imaginarius − мнимый).

Множество комплексных чисел обозначается C .

Комплексные числа не являются числами в обычном смысле слова, применяемыми при подсчётах и измерениях. Они образуют новый класс математических объектов, который определяется описанными ниже свойствами.

Определение 2. Два комплексных числа с₁ =(а₁,b₁) и c₂=(a₂,b₂) равны в том и только в том случае, если соответственно равны их действительные и мнимые числа, т.е. c₁ = c₂ , лишь если a₁ = a₂ , b₁ = b₂ .

Понятия «больше» и «меньше» для комплексных чисел не вводятся.

Определение 3. Комплексное число (0,1) называется мнимой единицей и обозначается символом i: i=(0,1).

Комплексное число (x ,0) отождествляется с действительным числом x : (x,0) = x . Комплексное число (0,y) называется мнимым числом. Комплексное число (0,0) называется нулём: (0,0) = 0. Число (1,0) =1 называется единицей.

Определение 4. Два комплексных числа c = (a,b) и c = (a,-b), имеющие одинаковые действительные и противоположные мнимые части, называются сопряжёнными комплексными числами.

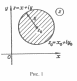Пусть ɛ > 0 - произвольное положительное число, а z₀ - произвольное комплексное число. Множество точек z комплексной плоскости, удовлетворяющих неравенству |z - z₀| < ɛ,

является открытым кругом радиуса ɛ с центром в точке z₀ (рис. 1).

В самом деле, полагая z₀ = x₀ + iy₀, z = x + iy,

получим |z - zo| = < ɛ,

или, возводя в квадрат, (x-x₀)² + (у - y₀)² < ɛ².

Совокупность точек z комплексной плоскости, удовлетворяющих неравенству |z – zo| < ɛ, будем называть ɛ - окрестностью точки z₀.

Точка z называется внутренней точкой множества на комплексной плоскости, если существует ɛ - окрестность этой точки, целиком принадлежащая данному множеству.

Областью на комплексной плоскости называется множество D точек, обладающих следующими свойствами:

1) каждая точка множества D является внутренней точкой этого множества (открытость);

2) любые две точки множества D можно соединить ломаной, состоящей из точек этого множества (связность).

Граничной точкой области D называется всякая точка z , в любой ɛ - окрестности которой содержатся как точки, принадлежащие области D, так и точки, не принадлежащие области D. Совокупность граничных точек называется границей области D. Обозначение: dD.

Область D с присоединенной к ней границей dD называется замкнутой областью и обозначается символом D .

Замкнутую кривую без самопересечений будем называть контуром. Всякий контур разбивает плоскость на две различные области и является границей каждой из них. Одна из этих областей - внутренность контура - ограничена, а другая – внешность контура - неограничена.

Область D будем называть односвязной, если внутренность любого контура, принадлежащего D, также принадлежит D. Область, не являющуюся односвязной, назовем многосвязной.

Функция комплексного переменного.

Будем говорить, что на множестве S комплексной плоскости z определена функция w = f(z), если указано правило, по которому каждому комплексному числу z из S ставится в соответствие комплексное число w .

Таким образом, функция w = f(z) осуществляет отображение точек комплексной плоскости z на соответствующие точки комплексной плоскости w (рис. 6)

Положим

z = x + iy, w = u + iv.

Тогда задание функции комплексного переменного w = f(z) будет равносильно заданию двух действительных функций двух действительных переменных u = u(z, у), v = v(z, у), где w = j(z) = u(z, у) + iv(z, у).

Функция u(x, у) называется действительной частью функции w = f(z) (Re w), а v(z, у) - ее мнимой частью (Im w).

Пример 3. Пусть w = z². Полагая z = x + iy, w = u + iv, получим u + iv = (z + iy)2 = z2 - у2 + i2zy.

Следовательно, равенство w = z² равносильно двум равенствам u = x² - y², v = 2xy.

Функция w = f (z) называется однолистной функцией на множестве S , если в разных точках этого множества она принимает разные значения. Функция, не являющаяся однолистной, называется многолистной.

Пример 4. Функция w = z² однолистна в верхней полуплоскости Im z > О и многолистна на всей плоскости. Например, i² = ( -i)² = - 1 .

Часто рассматривают многозначные функции комплексного переменного, когда каждому значению z из S ставится в соответствие несколько комплексных чисел.

Пример 5. Функция w = z двузначна на всей плоскости z, исключая нулевую точку (и бесконечно удаленную).

Кривые на комплексной плоскости.

Е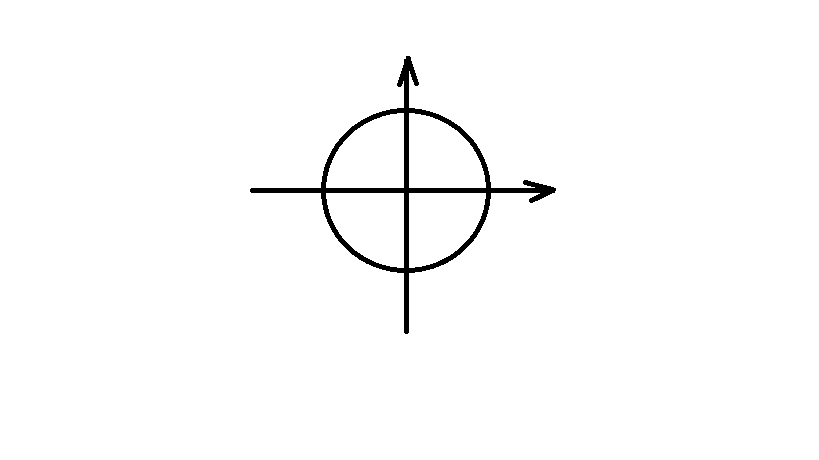 сли z=z(t)

x(t)=Re z(t)

y(t)=Im z(t)

z(t)=x(t)+ iy(t) (1) – параметрическое представление.

t₀ t T

Графиком является параметрическая кривая.

t₁,t₂ (t₀,T) – самопересекающейся кривой.

Совпадение концов не является самопересечением.

Нелинейные и несамопересекающая кривые называется Кривая Жордана. Кривая, у которой совпадают концы называется простой кривой.

Кривая называется кусочно-гладкой, если её можно разбить на конечное число гладких кривых.