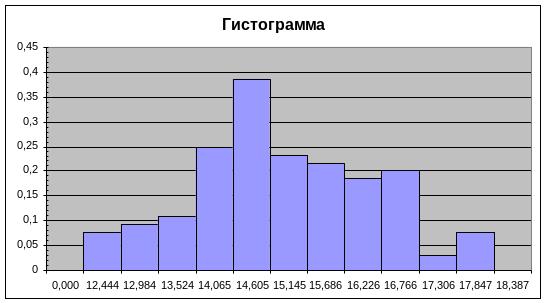
0. Гистограмма.

Статистический ряд часто оформляется графически в виде гистограммы.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы Δ, а высоты равны отношению (плотность частоты). Площадь гистограммы частот равна сумме частот, т.е. объему выборки.

Гистограммой относительных частот, называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы , а высоты равны отношению (плотность относительной частоты). Площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины Х

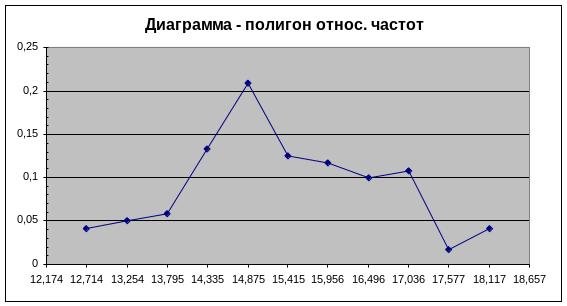
Полигоном частот называют ломаную, соединяющую точки с координатами , , …, .

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки с координатами , , …, .

1. Эмпирическая функция распределения

Номер интервала
1	-54,202	-42,971	-48,586	0,02	0,02	0,02
2	-42,971	-31,739	-37,355	0	0,02	0
3	-31,739	-20,508	-26,123	0,03	0,05	0,03
4	-20,508	-9,276	-14,892	0,06	0,11	0,06
5	-9,276	1,955	-3,660	0,17	0,28	0,17
6	1,955	13,187	7,571	0,14	0,42	0,14
7	13,187	24,418	18,802	0,21	0,63	0,21
8	24,418	35,650	30,034	0,12	0,75	0,12
9	35,650	46,881	41,265	0,08	0,83	0,08
10	46,881	58,113	52,497	0,09	0,92	0,09
11	58,113	69,344	63,728	0,05	0,97	0,05
12	69,344	80,575	74,960	0,03	1	0,03
Всего				1		1

Каждая генеральная совокупность имеет функцию распределения , которая обычно неизвестна. По выборке можно найти эмпирическую функцию распределения .

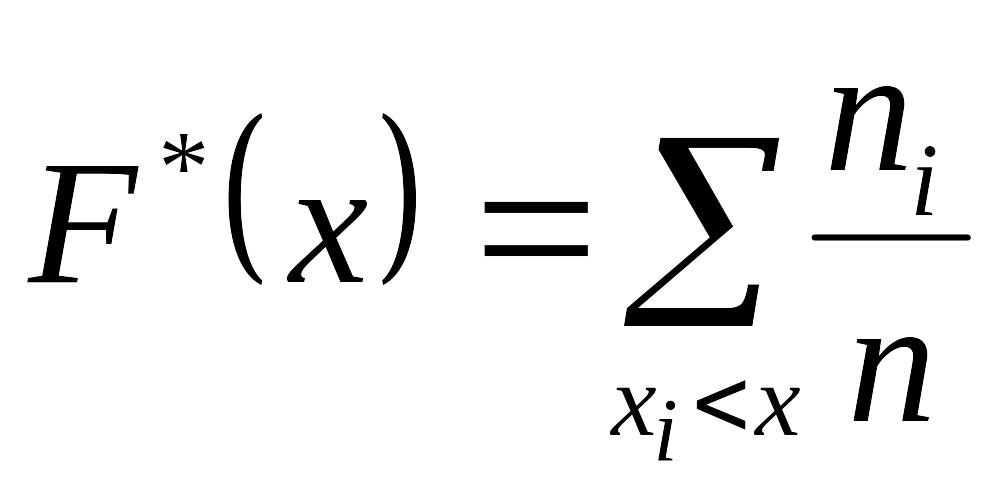0. Статистическая функция распределения.

Статистической функцией рапределения случайной величины Х называется частота события Х<х в данном статистическом материале

F*(x)=P*(X<x)

Для токо чтобы найти значение статистической функции распределения при данном х, достаточно подсчитать число опытов, в которых величина Х приняла значение, меньше чем х, и разделить на общее число n произведенных опытов.

Статистическая функция распределения любой случайной величины – прерывной или непрерывной – представляет собой прерывноую ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений. При увеличении числа опытов n, согласно теореме Бернулли, при любом х частота события Х<х приближается (сходится по вероятности) к вероятности этого события. Следовательно, при увеличении n статистическая функция распределения F*(x) прближается (сходится по вероятности) к подлинной функции распределения случайной величины Х.

Если Х – непрерывная случайная величина, то при увеличении числа наблюдений n число скачков функции F*(x) увеличивается, сами скачки уменьшаются и график функции F*(x) неограниченно приближается к плавной кривой F(x) – функции распределения величины Х.

6. Числовые характеристики статистического распределения.

Каждой числовой характеристике случайной величины Х соответствует ее статистическая аналогия. Для математического ожидания случайной величины аналогией является среднее арифметическое наблюденных значений случайной величины:

где x_i– значение случайной величины, наблюденное в i–м опыте, n– число опытов.

Эта характеристика называется статистическим средним случайной величины.

Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При достаточно большом n статистическое среднее может быть принято приближенно математическому ожиданию. При ограниченном числе опытов статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.

Подобные статистические аналогии существуют для всех числовых характеристик. Будем обозначать эти статстические аналогоии теми же буквами, что и соответствующие числовые характеристики, но снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она представляет собой математическое ожидание случайной величины :

Если в этом выражении заменить математическое ожидание его статистической аналогией – средним арифметическим, мы получим статистическую дисперсию случайной величины Х:

где m_x*=M*[X]– статистическое среднее.

Аналогично определяются статистические начальные и центральные моменты любых порядков:

Все эти определения полностю аналогичны определениям числовых характеристик случайной величины. С той разницей, что в них везде вместо математического ожидания фигурирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном n могут быть приняты приближенно равными им.

Нетрудно доказать, что для статистических начальных и центральных моментов справедливы те же свойства, которые были выведены для математических моментов. В частности, статистический первый центральный момент всегда равен нулю:

Соотношения между центральными и начальными моментами также сохраняются:

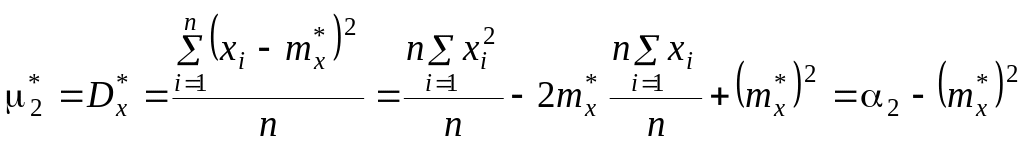
При очень большом количестве опытов вычисление характеристик по приведенным выше формулам становится чрезмерно громоздким, и можно применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характеристики будут выражаться приближенными формулами:

где – «представитель» i-го разряда, p_i*– частота i–го разряда, k – число разрядов.

Как видно, эти формулы полностью аналогичны формулам, определяющим математическое ожидание, дисперсию, начальные и центральные моменты дискретной случайной величины Х, с той только разницей, что вместо вероятностей в них стоят частоты, вместо математического ожидания – статистическое среднее , вместо числа возможных значений случайной величины – число разрядов.